因为f(z)在B内解析,所以f(z)在B内连续, 故He>0,6>0, 使得满足5-z<6的一切5都在K内, 即△z<6时,总有f(5)-f(z<e, 由积分的估值性质, F(A)-F(-(Y B △z 2:44:26
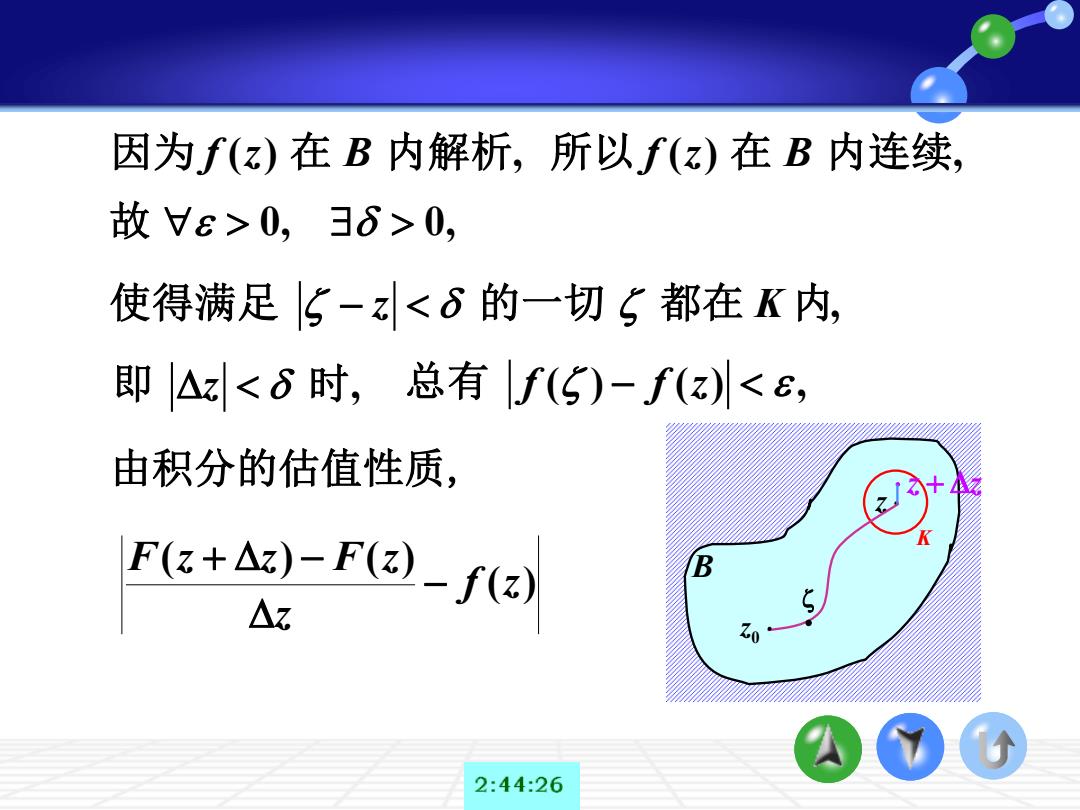
B z K z + z 0 z • 因为 ( ) , f z B 在 内解析 所以 ( ) , f z B 在 内连续 故 0, 0, 使得满足 , − z K 的一切 都在 内 即 , z 时 总有 ( ) ( ) , f f z − 由积分的估值性质, ( ) ( ) ( ) f z z F z z F z − + −

Ee+a如-a-eF应*60-aa5 △z k起上fg-faus如6ac=s 于是 lim △z→0 Fz+)-F@-fe=0, △z 即F(z)=f(z). [证毕] 此定理与微积分学中的对变上限积分的求导 定理完全类似 2:44:26
( ) ( ) ( ) f z z F z z F z − + − [ ( ) ( )]d 1 f f z z z z z − = + | ( ) ( )| d 1 f f z z z z z − + . 1 = z z 0 ( ) ( ) lim ( ) 0, z F z z F z f z → z + − − = 于是 即 ( ) ( ). F z f z = 此定理与微积分学中的对变上限积分的求导 定理完全类似. [证毕]