
二、线性分组码的严格数学定义4 由第2章定理3可知,必存在k个线性独立的码字g192,,9k,使∀c∈CH c=mn-191+mn-292+...+mn-kgk =m G 基不同,G不同,但 生成的空间是一样的, 不同的G的意义是什 91,n-191,n-2…g1,0 么? G= 92.n-192,n-2…92.0 gkn-19kn-2…9k,0 秩是多少? G称为[n,k]码的生成矩阵。 G的标准形式kP],称为典型生成矩阵
二、线性分组码的严格数学定义4 由第2章定理3可知,必存在k个线性独立的码字g1 , g2 , … , gk , 使cCH: c=mn-1g1+mn-2g2+… + mn-kgk =m G g1,n-1 g1,n-2 … g1,0 g2,n-1 g2,n-2 … g2,0 .......... gk,n-1 gk,n-2 … gk,0 G= G称为[n,k]码的生成矩阵。 G的标准形式[IkP], 称为典型生成矩阵。 基不同,G不同,但 生成的空间是一样的, 不同的G的意义是什 么? 秩是多少?

三、G与H的关系 G的行矢量是码字,HgT=0T,有HGT=0T,H与G所张成的空间互为零空间。 CH:H校验,G生成 CG:G校验,H生成。j 互为对偶码,若Cu=Cc,则称为自对偶码(P62) [Q In-K][lkP]T=[QIn-k][lKT PT]T=Q+PT =0 所以P=-QT或Q=PT 由此得G=[kP]=[lkQ门 H=[Q In-K]=[-PT In-k]
三、G与H的关系 G的行矢量是码字,Hgi T=0 T , 有HGT= 0 T, H与G所张成的空间互为零空间。 CH: H校验,G生成。 CG: G校验,H生成。 互为对偶码,若CH=CG, 则称为自对偶码(P62) [Q In-k ] [IkP]T= [QIn-k ] [Ik T PT] T= Q + PT = 0 所以 P= - QT 或 Q = -PT 由此得 G=[Ik P] = [ Ik –QT] H=[Q In-k ]= [ -PT In-k ]

三、G与H的关系2 例:已知[7,3]码(p52,例3.1) :1011000 0100 H= :111 1100010 011:0001 C=(C6C5C4C3C2C1Co) 由HcT=0T得 C3=C6+C4 C2=C6+C5+C4 C1=C6+C5 C0=C5+C4 1110 1001110 P=-QT= 0111 G=[lk P]= 010|0111 1101 001|1101
三、G与H的关系2 例: 已知[7,3]码(p52, 例3.1) 1 0 1 | 1 0 0 0 1 1 1 | 0 1 0 0 1 1 0 | 0 0 1 0 0 1 1 | 0 0 0 1 H= c=(c6c5c4c3c2c1c0 ) 由Hc T=0 T得 c3=c6+c4 c2=c6+c5+c4 c1=c6+c5 c0=c5+c4 1 1 1 0 0 1 1 1 1 1 0 1 P= -QT= G=[Ik P] = 1 0 0 | 1 1 1 0 0 1 0 | 0 1 1 1 0 0 1 | 1 1 0 1
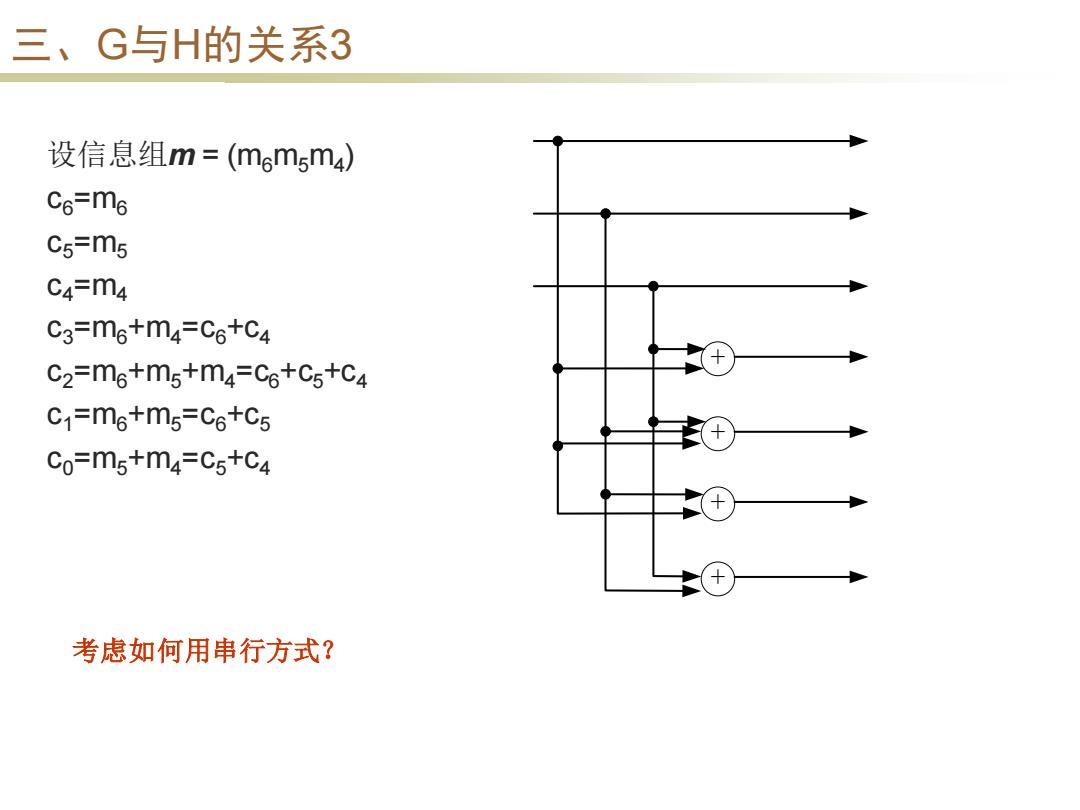
三、G与H的关系3 设信息组m=(memsm4) C6=m6 c5=m5 C4=m4 C3=m6+m4=C6+C4 C2=m6+m5+m4=C6+C5+C4 C1=m6+m5=C6+C5 Co=m5+m4=C5+C4 考虑如何用串行方式?
三、G与H的关系3 设信息组m = (m6m5m4 ) c6=m6 c5=m5 c4=m4 c3=m6+m4=c6+c4 c2=m6+m5+m4=c6+c5+c4 c1=m6+m5=c6+c5 c0=m5+m4=c5+c4 + + + + 考虑如何用串行方式?
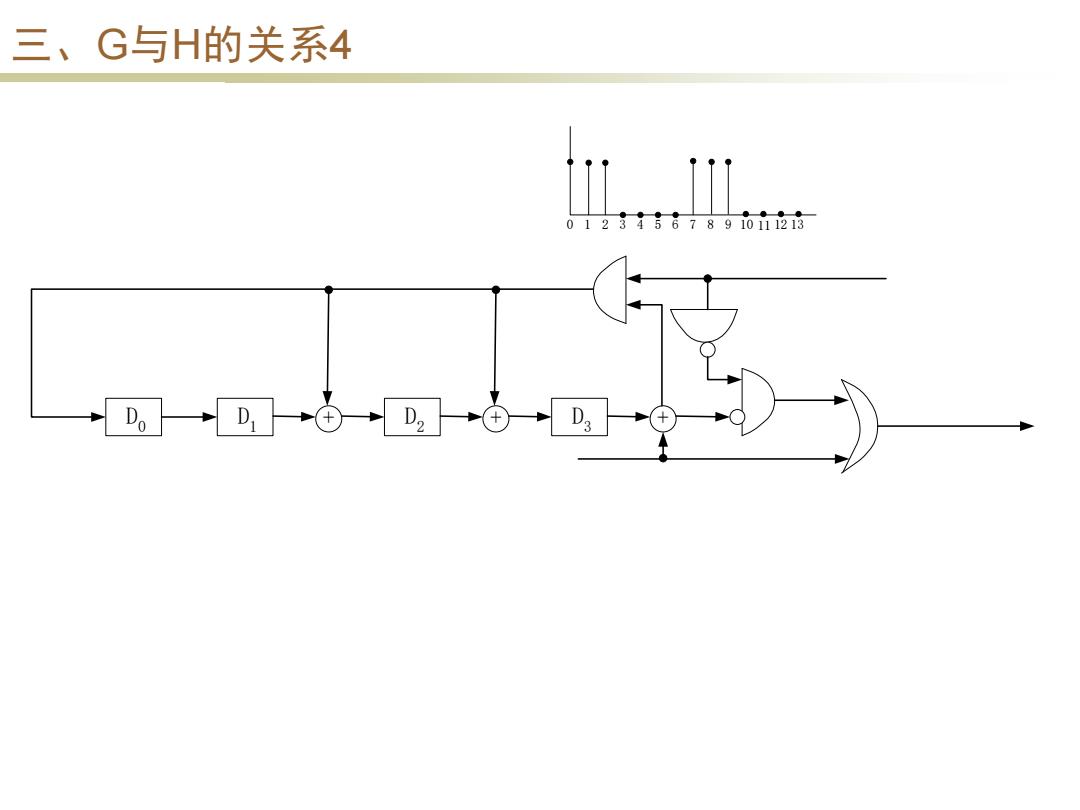
三、G与H的关系4 0123487890218 Do D2 2
三、G与H的关系4 + + + 0 1 2 3 4 5 6 7 8 9 10 11 12 13 D0 D1 D2 D3