
第四章多项式与有限域 陆以勤 -一一--一一--一一--一一-
第四章 多项式与有限域 陆以勤

米学习本章目的:对Xn-1进行因式分解(n=gm-1,q为素数) X15-1=(x+1)(x4+x3+1)(x4+x3+x2+x+1)(x2+x+1)(x4+x+1) 米Xn-1? 循环:只有最高位和最低位
学习本章目的:对X n-1进行因式分解(n=qm-1,q为素数) X 15-1=(x+1)(x 4 + x 3+1)(x 4+x3+x2 +x +1)(x 2 +x +1)(x 4+x +1) X n-1? 循环:只有最高位和最低位

一、剩余类环 1. 环,子环、扩环 回顾环(R,+,*)的定义 米定义了两种运算+和* 米 R对+构成阿贝尔群 米 *满足封闭性、结合律 米 *对+满足分配律 米 *不一定有恒等元1,R的元素不一定有逆元 2. 非空子集S是环(R,+,*)的子环的充要条件: 1)Va,beS:a-b∈S;S是群(R,+)的子群 2)Va,beS:ab∈SS对*满足封闭性
一、剩余类环 1. 环,子环、扩环 回顾环(R,+, *)的定义 定义了两种运算+和* R对+构成阿贝尔群 *满足封闭性、结合律 *对+满足分配律 *不一定有恒等元1,R的元素不一定有逆元 2. 非空子集S是环(R,+, *)的子环的充要条件: 1) a,b S:a-b S ; S是群(R,+)的子群 2) a,b S:ab S S对*满足封闭性

一、剩余类环 3。 理想 定义:交换环冲的非空子集/称为冲的理想,若: l)Ha,b∈I:a-b∈I; 2)Ha∈/,r∈R.ar=ra∈I, )+2)三理想是个子环, 2)三/中任一元素a的倍数在/中,即/由的一些元素 (可以是多个)的倍数组成。 米 主理想:由一个元素的的所有倍数组成的理想.这 个元素叫生成元. 米 主理想环:每一个理想都是主理想
一、剩余类环 3. 理想 定义: 交换环R中的非空子集I称为R中的理想,若: 1) a, b I: a-b I; 2) a I, r R: ar =ra I; 1)+2) 理想是个子环, 2) I 中任一元素a的倍数在I中,即I由R的一些元素 (可以是多个)的倍数组成。 主理想:由一个元素的的所有倍数组成的理想.这 个元素叫生成元. 主理想环:每一个理想都是主理想
一、剩余类环 4. 剩余类环 定理1(定理4.1.2):设/为可换环R的一个理 ,则R/1构成一个可换环,称为模/的剩余类 环 例:Mod5的剩余类环 {0}: 0 5 -5 10 -10 1+1 {1}: 1 6 -4 11 -9 2+1{2}: 2 7 -3 12 -8 3+1{3}: 3 8 -2 13 -7 4+1{4}: 4 9 一1 14 -6 {{0},{1},{2},{3},{4}}对模5+和模5*构成可换环
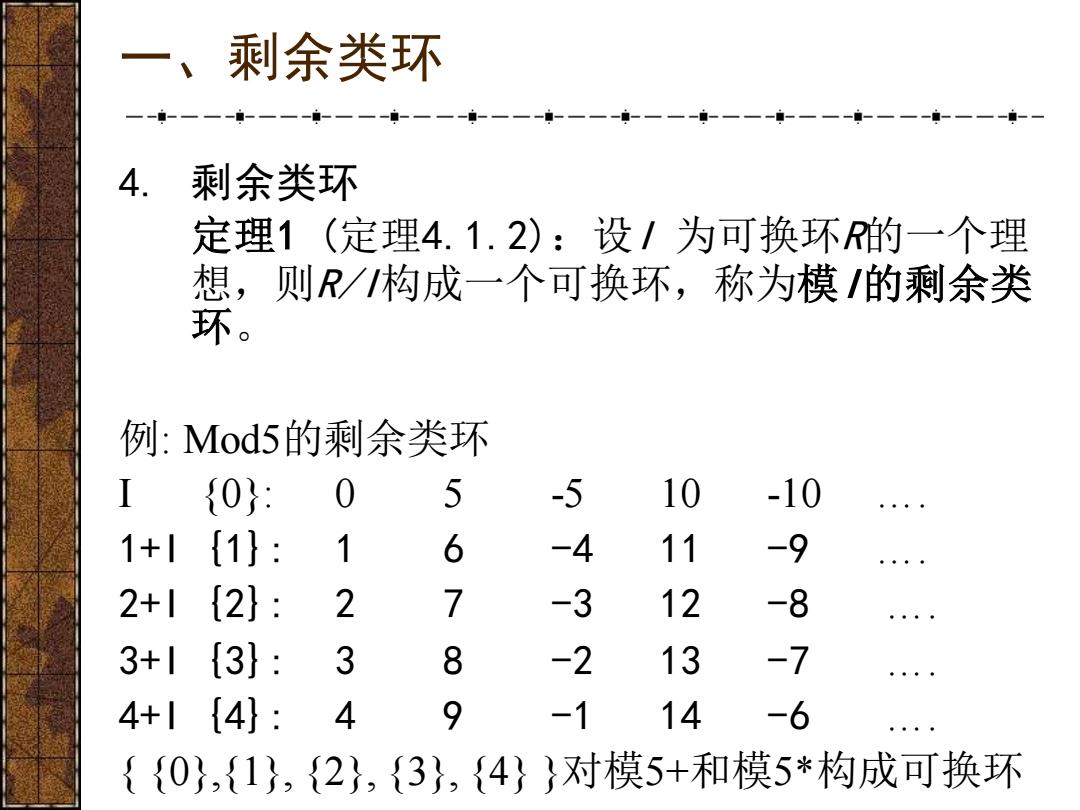
一、剩余类环 4. 剩余类环 定理1 (定理4.1.2):设I 为可换环R的一个理 想,则R/I构成一个可换环,称为模I的剩余类 环。 例: Mod5的剩余类环 I {0}: 0 5 -5 10 -10 …. 1+I {1}: 1 6 -4 11 -9 …. 2+I {2}: 2 7 -3 12 -8 …. 3+I {3}: 3 8 -2 13 -7 …. 4+I {4}: 4 9 -1 14 -6 …. { {0},{1}, {2}, {3}, {4} }对模5+和模5*构成可换环