华南理工大学：《现代编码理论与技术》课程教学资源（PPT课件讲稿）第六章 循环码的译码

第六章循环码的译码 陆以勤 2005年5月

第六章 循环码的译码 陆以勤 2005年5月

一、循环码译码的原理 线性分组码的译码：标准阵列译码，伴随式译码 译码电路复杂 r→s计算电路 s→e译码表 r-e电路

一、循环码译码的原理 ◼ 线性分组码的译码：标准阵列译码，伴随式译码 译码电路复杂 r→s计算电路 s→e译码表 r- e电路 ....... r c

一、循环码译码的原理-线性分组码中求伴随式的电路 1110100 例1：[7,4,3]循环汉明码，g(X)=x3+x+1,H= 0111010 1101001 T 1110100 s=rHT=(rers r4r3r2rro) 0111010 fo+rs+ra+r2T(2S0) r5+r4+r3+r1 1101001 r6+r5+r3+ro ro r r2 4 r(x) 60 S2

一、循环码译码的原理----线性分组码中求伴随式的电路 例1：[7,4,3] 循环汉明码，g(x)=x3+x+1,H= 1110100 0111010 1101001 s = r HT= ( r6 r5 r4 r3 r2 r1 r0 ) T r6 + r5 + r4 + r2 r5 + r4 + r3 + r1 r6 + r5 + r3 + r0 = T = （s2 s1 s0 ) r0 + r1 r 2 r 3 r 4 r 5 r 6 + + r(x) s0 s1 s2 1110100 0111010 1101001

一、循环码译码的原理--利用循环码的特殊性简化电路 s=rHT H=[-PTIn-k]=[-(1(X)T-(r2(X)T..-(k(X)Tn-k] 其中，r,x)=-xni(modg(x)(i=1,2…,。 x-1 x-2 HT≡ x- ≡Ln] 七-k-l mod g(x) 1 s≡HT=r(modg(x) s(X)≡rx)≡(c(x)+e(x)≡e(X)(modg(X) 定理1：由g(X)生成的循环码，()的伴随式s()满足： s(x)=r(x)=e(x)(mod g(x)) 因此，求S(x)可用除以gx的电路实现。这样可把n级寄存器降为n-k级

一、循环码译码的原理----利用循环码的特殊性简化电路 ◼ s  rHT H=[-P T In-k ]=[-(r1 (x))T -(r2 (x))T…-(rk (x))T In-k ] 其中，ri (x)  - x n-i (mod g(x)) (i=1,2,...,k)。 [I ] 1 ... ... H n 1 2 1 T                         − − − − − n k n k n n x x x x mod g(x) s  rHTr (mod g(x)) s(x) r(x)  (c(x)+e(x))  e(x) (mod g(x)) 定理1：由g(x)生成的循环码，r(x)的伴随式s (x)满足： s(x) r(x)  e(x) (mod g(x)) 因此，求S (x)可用除以g(x)的电路实现。这样可把n级寄存器降为n-k级

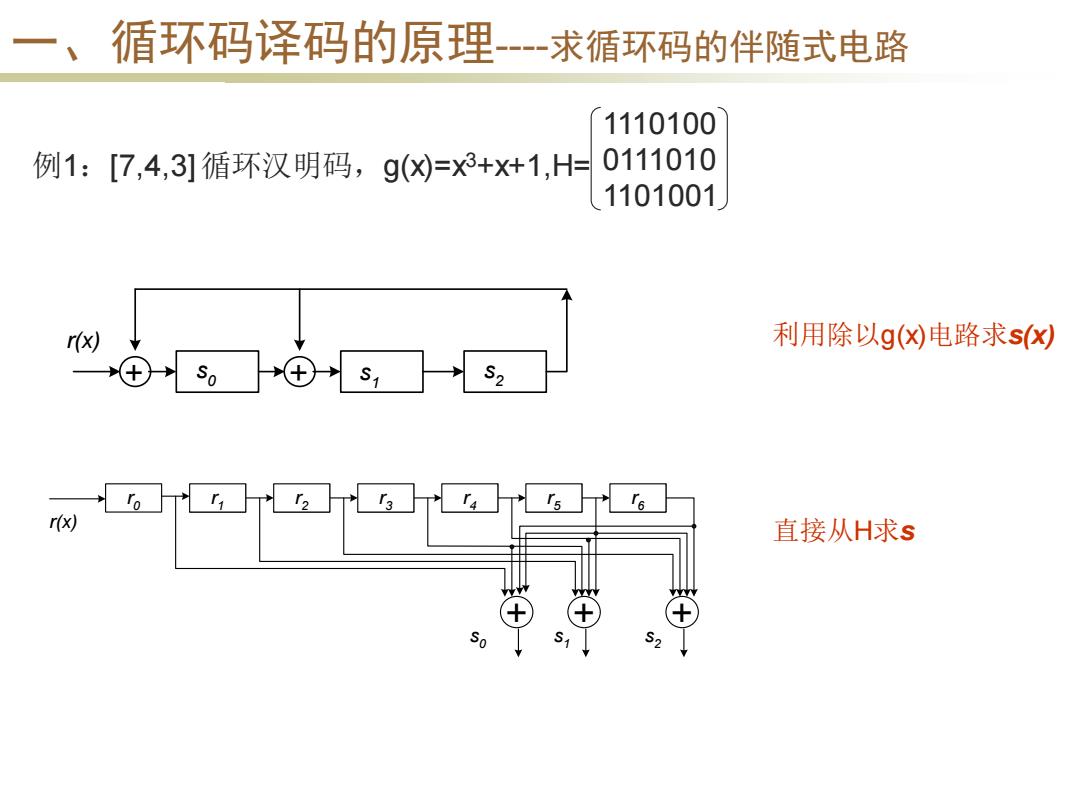
一、循环码译码的原理--求循环码的伴随式电路 1110100 例1：[7,4,3]循环汉明码，g()=x3+x+1,H= 0111010 1101001 r(x) 利用除以g()电路求s(x) So 52 r(x) 直接从H求s So S1

一、循环码译码的原理----求循环码的伴随式电路 r0 + r1 r 2 r 3 r 4 r 5 r 6 + + r(x) s0 s1 s2 例1：[7,4,3] 循环汉明码，g(x)=x3+x+1,H= 1110100 0111010 1101001 + + r(x) s0 s1 s2 直接从H求s 利用除以g(x)电路求s(x)