
第十三章Turboi码 陆以勤
第十三章 Turbo码 陆以勤
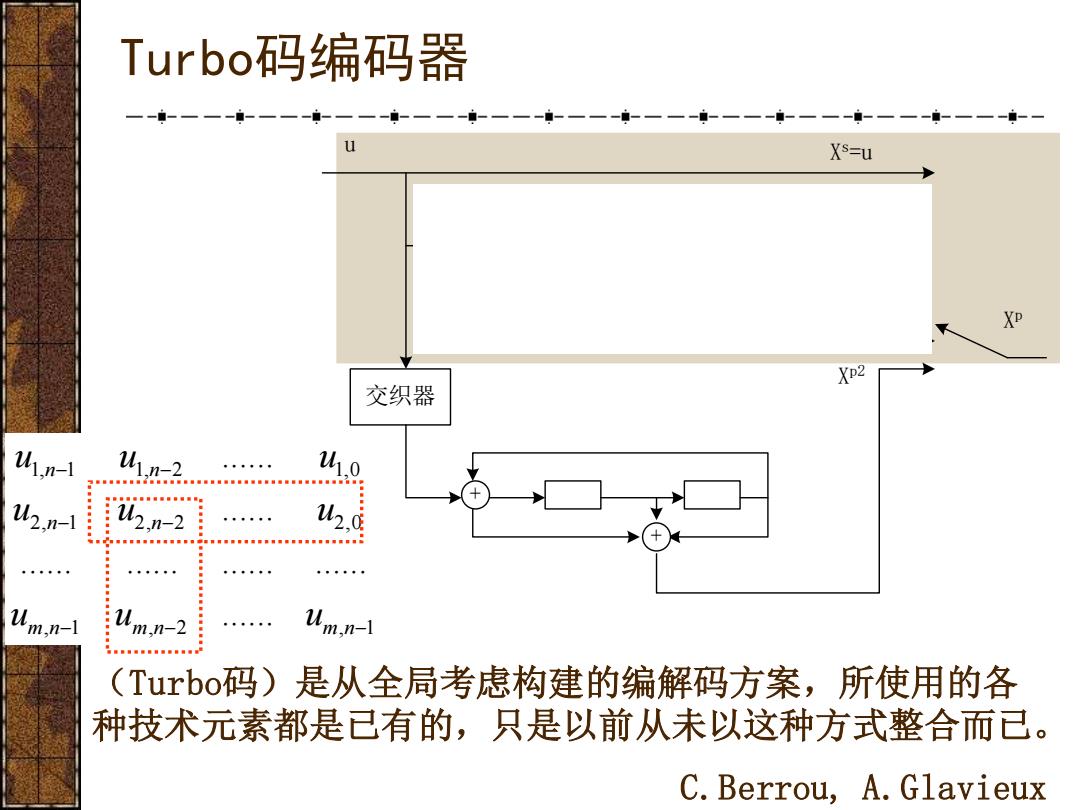
Turbo码编码器 Xs=u XP XP2 交织器 4,n- U 1,n-2 .外 男年0用年用用用是g用图里。 U2,n-1月 2,n-2 1110n1日 Um.n-1 :u. m,n-2 Um.n-1 EAMnEEMnnana (Turbo码)是从全局考虑构建的编解码方案,所使用的各 种技术元素都是已有的,只是以前从未以这种方式整合而已。 C.Berrou,A.Glavieux
Turbo码编码器 + + 交织器 + + Xs=u Xp1 Xp2 Xp u (Turbo码)是从全局考虑构建的编解码方案,所使用的各 种技术元素都是已有的,只是以前从未以这种方式整合而已。 C.Berrou, A.Glavieux , 1 , 2 , 1 2, 1 2, 2 2,0 1, 1 1, 2 1,0 ...... ...... ...... ...... ...... ...... ...... − − − − − − − m n m n m n n n n n u u u u u u u u u

设2LwP L(ug)= P(44=0,(y,2,,yw》/P(04,2,yw》 ∑P(e,04,h,yw》 P(44=1,(0y,y2,yv》 e,uk= P(uk=0,(0y1,2,,yN) ∑P(e,(y,2,yx》 e,k=0 根据BCR算法(课本参考文献[12]) P(e,(,》码块为(yy2,y)同时在k时刻分支为e的概率 =P(sg(e),(y,2,,yk-i》P(s(e),yg/s-(e》P(yk+1yk+2,yw)/s(e》 x(S)=P(s,(y,2,,y) Y(e)=P(s(e).v:Isj(e)) 注意:s(e)=s(e)s-(e) B()=P(yk+1,yk+2,,yN)/S) e P(e,(y,2,,yw))=&k-1(s(e)y(e)B(s(e) i-(e),ck-1(e) >a(s(e)r:(e)B(sj(e)) Sk-s(e)… L(ug)=In e,k=] ∑a4-(s-(e7(e)p,(s(e) k-1时刻 k时刻 e,ug =0
= = = = = = = = = = = = = − = − − + + − − − − − − + + = = , 0 1 1 , 1 1 1 1 2 1 1 1 2 1 1 1 1 2 1 1 2 1 1 1 2 1 2 , 0 1 2 , 1 1 2 1 2 1 2 1 2 1 2 1 2 1 2 ( ( )) ( ) ( ( )) ( ( )) ( ) ( ( )) ( ) ln ( ,( , ,...,, )) ( ( )) ( ) ( ( )) ( ) (( , ,...,, )/ ) ( ) ( ( ), / ( )) ( ) ( ) ( ) ( ,( , ,...,, )) ( ( ),( , ,...,, )) ( ( ), / ( )) (( , ,...,, )/ ( )) ( ,( , ,..., )) BCJR [12]) ( ,( , ,...,, )) ( ,( , ,...,, )) ln ( 0,( , ,...,, )) ( 1,( , ,...,, )) ln ( 0,( , ,...,, ))/ (( , ,...,, )) ( 1,( , ,...,, ))/ (( , ,...,, )) ( ) ln k k k k e u S k k k S k k e u S k k k S k k k S k k k S N k k k k k N S k E k S k k E k k k k S k k N k S k k S k k S k N e u N e u N k N k N k N N k N N k s e e s e s e e s e L u P e y y y s e e s e s P y y y s e P s e y s e s e s e s P s y y y P s e y y y P s e y s e P y y y s e P e y y y P e y y y P e y y y P u y y y P u y y y P u y y y P y y y P u y y y P y y y L u - - = - 注意: = 根据 算法(课本参考文献 设yk=(y s k , y p k ) 码块为(y1,y2 ,…., yN)同时在k时刻分支为e的概率 Sk-1 S(e) SE k-1(e) k-1时刻 k时刻 e uk-1(e),ck-1(e)

ak(s)=P(s ,(yi,y22...,)) 前k个码字为y1,y2,,y)同时在k时刻到达状态为s的概率 体现了时刻k之前的码元对当前信息位,的影响 Y:(e)=P(sk(e),ygIs(e)) 注意:s(e)=s(e) 在k-1时刻到达状态为s,(e)的条件下,信息比特为y,同时时刻 转移到状态s1(e) rk(e)=P(s(e)/s(e))P(ygIs(e),s(e))=P(ug)P(yg/ux) B(s)=P((vk,yk+2....Yx)/s 接收码 y1 y2 Yk+2 时刻012 kk+1 N 在时刻到达状态为s的条件下 后N-k个码字为(yk+1,yk+2,,yN)的概率 S-(e) 体现了时刻k之后的码元对当前信息位,的影响 P(e,(Y1,Y2>....Yx))=ak-(s(e)r(e)B:(sj(e)) 由于充分考虑了前后的信息,因此误码率大大降低
由于充分考虑了前后的信息,因此误码率大大降低 = 体现了时刻 之后的码元对当前信息位 的影响 后 个码字为 的概率 在 时刻到达状态为 的条件下 转移到状态 在 时刻到达状态为 的条件下,信息比特为 ,同时 时刻 注意: = 体现了时刻 之前的码元对当前信息位 的影响 前 个码字为 同时在 时刻到达状态为 的概率 ( ,( , ,...,, )) - ( ( )) ( ) ( ( )) ( , ,...,, ) ( ) (( , ,...,, )/ ) ( ) ( ( )/ ( )) ( / ( ), ( )) ( ) ( / ) ( ) 1 ( ) ( ) ( ( ), / ( )) ( ) ( ) ( , ,...,, ) ( ) ( ,( , ,...,, )) 1 2 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 1 2 1 2 P e y y y s e e s e k u N k y y y k s s P y y y s e P s e s e P y s e s e P u P y u s e k s e y k e P s e y s e s e s e k u k y y y k s s P s y y y S k k k S N k k k k k N k k k N k k k S k E k k S k E k k E k k S k S k E k S k k E k k k k k k − + + + + − − − − − − − − − − = = = − = = 0 1 2 …… k-1 k k+1 …… N Sk-1 S(e) SE k-1(e) 时刻 接收码 y1 y2 …… yk-1 yk yk+1 yk+2 ……yN e uk-1(e)

e.04)4-@rea.e ax(S)=P(s,(yiy2>....)) SE(e) Y:(e)=P(s(e).yx/s(e)) 注意:s(e)=s(e) ⊙ f(S)=P(yk+1,yk+2,,yN)/s)) ux(e),Cx(e) 考虑到分量编码器相当于马尔可夫源 S.S(e) a4(s2(e》=P(s2(e),(y,2,y》 k时刻 k十1时刻 =∑P(s(ehsE(e),(yy2,,y)》 =∑P(s(eh0,y2,yk-P(s是(ey/s(e)》s.e =∑ak-(s(e)M(e) k-1e),Ck-(e) B-(s(e))=P((yxx)/(e)) S-s(e) =∑P(s(e)(0yk,yk+2,yw)/s-(e》 k-1时刻 k时刻 =∑P(yk+,k+2,yw)/s(e)P(si(e),y/sai(e》 =∑B.(s(e)m(e)
( ( )) ( ) (( , ,...,, )/ ( )) ( ( ), / ( )) ( ( ) ( , ,...,, )/ ( )) ( ( )) (( , ,...,, )/ ( )) ( ( )) ( ) ( ( ) ( , ,...,, )) ( ( ), / ( ))) ( ( ) ( ),( , ,...,, )) ( ( )) ( ( ),( , ,...,, )) ( ) (( , ,...,, )/ ) ( ) ( ( ), / ( )) ( ) ( ) ( ) ( ,( , ,...,, )) ( ,( , ,...,, )) ( ( )) ( ) ( ( )) 1 2 1 1 2 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 2 1 2 1 1 1 1 2 1 2 1 1 s e e P y y y s e P s e y s e P s e y y y s e s e P y y y s e s e e P s e y y y P s e y s e P s e s e y y y s e P s e y y y s P y y y s e P s e y s e s e s e s P s y y y P e y y y s e e s e k e S k k S k k E k e S k k N k e S k k N k S k S k k N k S k k k e S k k S k k E k e k S k e k E k S k k E k S k k k k k N S k E k S k k E k k k k S k k k S N k k = = = = = = = = = + + − − + − − − + − − − − − − − − − − + + − − − − = , , = , 考虑到分量编码器相当于马尔可夫源 注意: = = - Sk S(e) Sk E(e) k时刻 k+1时刻 e uk (e),ck (e) Sk-1 S(e) SE k-1(e) k-1时刻 k时刻 e uk-1(e),ck-1(e)