
教案第二章牛顿定律 dimo=LMTS 在一个等式的两边,量纲必须相同,故一般可用量纲来初步检查等式的正确性。 国际单位制的基本单位有七个,其定义如下: 1)长度:米是光在真空中(1299792458)s时间间隔内是经路径的长度: 2)质量:千克等于国际千克原器的质量: 3)时间:秒是绝-133原子基态的两个超精细能级之间跃迁所对应的辐射的9192631770 个周期的持续时间: 4)电流:在真空中,截面积可忽略的两根相距1m的无限长平行圆直导线内通以等量恒 定电流时,若导线间相互作用力在每米长度上为2x10N,则每根导线中的电流为1A: 5)热力学温度:热力学温度开尔文是水三相点热力学温度的1273.16: 6)物质的量:摩尔是一系统的物质的量,该系统中所包含的基本单元数与0.012kg碳-12 的原子数目相等。在使用摩尔时,基本单元应指明,可以是原子、分子、离子、电子及 其它粒子,或是这些粒子的特定组合: 7)发光强度:坎德拉是一光源在给定方向上发光强度,该光源发出频率为540x102Hz 的单色辐射,且在此方向上的辐射强度为(1/683)W/sr。 s3几种常见的力The forces ofnature 在动力学中,分析物体受力情况是十分重要的。力学中常见的力有弹性力、摩擦力、 万有引力等,它们分属不同性质的力,弹性力和摩擦属接触力,而万有引力属场力。下 面我们来介绍弹性力、摩擦力和万有引力。 一万有引力 牛顿继承了前人的研究成果,提出了著名的万有引力定律。这个定律指出,星体之 间,地球与球表面附近的物体之间,以及所有物体与物体之间都存在着一种相互吸引的 力,所有这些力都遵循同一规律,这种相互吸引力叫做万有引力。万有引力定律可表达 为:在两个相距为”质量为m、m的质点间有万有引力,其方向沿着它们的连线,其 大小与它们的质量乘积成正比,与它们之间距离,的二次方成反比,即 19
教案 第二章 牛顿定律 19 p q S dimQ = L M T 在一个等式的两边,量纲必须相同,故一般可用量纲来初步检查等式的正确性。 国际单位制的基本单位有七个,其定义如下: 1)长度:米是光在真空中(1/299792458)s 时间间隔内是经路径的长度; 2)质量:千克等于国际千克原器的质量; 3)时间:秒是铯−133 原子基态的两个超精细能级之间跃迁所对应的辐射的 9192631770 个周期的持续时间; 4)电流:在真空中,截面积可忽略的两根相距 1m 的无限长平行圆直导线内通以等量恒 定电流时,若导线间相互作用力在每米长度上为 210−7N,则每根导线中的电流为 1A; 5)热力学温度:热力学温度开尔文是水三相点热力学温度的 1/273.16; 6)物质的量:摩尔是一系统的物质的量,该系统中所包含的基本单元数与 0.012kg 碳−12 的原子数目相等。在使用摩尔时,基本单元应指明,可以是原子、分子、离子、电子及 其它粒子,或是这些粒子的特定组合; 7)发光强度:坎德拉是一光源在给定方向上发光强度,该光源发出频率为 54010Hz 的单色辐射,且在此方向上的辐射强度为(1/683)W/sr。 §3 几种常见的力 The forces of nature 在动力学中,分析物体受力情况是十分重要的。力学中常见的力有弹性力、摩擦力、 万有引力等,它们分属不同性质的力,弹性力和摩擦属接触力,而万有引力属场力。下 面我们来介绍弹性力、摩擦力和万有引力。 一 万有引力 牛顿继承了前人的研究成果,提出了著名的万有引力定律。这个定律指出,星体之 间,地球与球表面附近的物体之间,以及所有物体与物体之间都存在着一种相互吸引的 力,所有这些力都遵循同一规律,这种相互吸引力叫做万有引力。万有引力定律 ...........可表达 为:在两个相距为 ......r.,质量为 ...m.1.、.m.2.的质点间有万有引力 .........,其方向沿着它们的连线 ..........,其. 大小与它们的质量乘积成正比 .............,与它们之间距离 .......r 的二次方成反比 .......,即
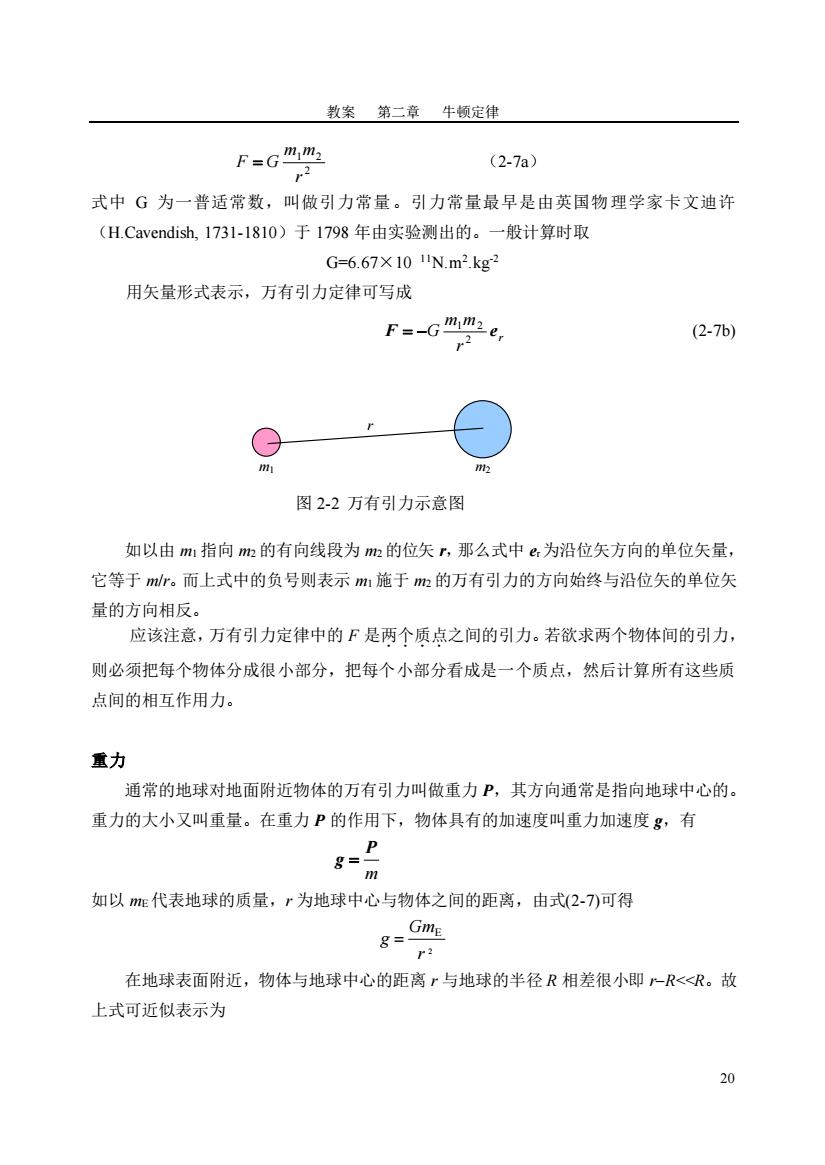
教案第二章牛顿定律 F=GM (2-7a) 式中G为一普适常数,叫做引力常量。引力常量最早是由英国物理学家卡文迪许 (H.Cavendish,1731-1810)于1798年由实验测出的。一般计算时取 G=6.67×101lN.m2kg2 用矢量形式表示,万有引力定律可写成 F=Gme (2-7b) G 图2-2万有引力示意图 如以由m指向m的有向线段为m的位矢,那么式中(为沿位矢方向的单位矢量 它等于m。而上式中的负号则表示m:施于m的万有引力的方向始终与沿位矢的单位矢 量的方向相反。 应该注意,万有引力定律中的F是两个质点之间的引力。若欲求两个物体间的引力, 则必须把每个物体分成很小部分,把每个小部分看成是一个质点,然后计算所有这些质 点间的相互作用力。 重力 通常的地球对地面附近物体的万有引力叫做重力P,其方向通常是指向地球中心的。 重力的大小又叫重量。在重力P的作用下,物体具有的加速度叫重力加速度g,有 8- 如以代表地球的质量,r为地球中心与物体之间的距离,由式(2-7)可得 在地球表面附近,物体与地球中心的距离r与地球的半径R相差很小即”R<R。故 上式可近似表示为
教案 第二章 牛顿定律 20 2 1 2 r m m F = G (2-7a) 式中 G 为一普适常数,叫做引力常量。引力常量最早是由英国物理学家卡文迪许 (H.Cavendish, 1731-1810)于 1798 年由实验测出的。一般计算时取 G=6.67×10 11N.m2 .kg-2 用矢量形式表示,万有引力定律可写成 r r m m F G e 2 1 2 = − (2-7b) 如以由 m1 指向 m2 的有向线段为 m2 的位矢 r,那么式中 er为沿位矢方向的单位矢量, 它等于 m/r。而上式中的负号则表示 m1 施于 m2 的万有引力的方向始终与沿位矢的单位矢 量的方向相反。 应该注意,万有引力定律中的 F 是两个质点 ....之间的引力。若欲求两个物体间的引力, 则必须把每个物体分成很小部分,把每个小部分看成是一个质点,然后计算所有这些质 点间的相互作用力。 重力 通常的地球对地面附近物体的万有引力叫做重力 P,其方向通常是指向地球中心的。 重力的大小又叫重量。在重力 P 的作用下,物体具有的加速度叫重力加速度 g,有 m P g = 如以 mE 代表地球的质量,r 为地球中心与物体之间的距离,由式(2-7)可得 2 E r Gm g = 在地球表面附近,物体与地球中心的距离 r 与地球的半径 R 相差很小即 r−R<<R。故 上式可近似表示为 m1 m2 r 图 2-2 万有引力示意图

教案第二章牛顿定律 g=0 二弹性力 当两物体相互接触而挤压时,它们要发生形变。物体形变时欲恢复原来的形状,物 体间会有作用力产生。这种物体因形变而产生欲使其恢复原来形状的力叫做弹性力。 常见的弹性力有:弹簧被拉伸或压缩时产生的弹簧弹性力:绳索被拉紧时所产生的 张力:重物放在支承面上产生的压力(作用在支承面上)和支持力(作用在物体上)等。 图2-4弹性力示意图 例题1 质量为m、长为1的柔软细绳,一端系着放在光滑 桌面上质量为m的物体,如图2-2(a)所示,在绳的另一 端加如图所示的F。绳被拉紧时会略有伸长(形变),一般 伸长甚微,可略去不计。现设绳的长度不变,质量分布 图2-5a 是均匀的。求:(1)绳作用在物体上的力:(2)绳上任意点的张力。 解如图2-2(b)所示,设想在绳索上点P将绳索分为 两段,它们之间有拉力F和F作用,这一对拉力称为张 力,它们的大小相等、方向相反。 ()由题意知,绳和物体均被约束在如图(©)所示的Ox 图2-5b) 轴上运动,且绳的长度不变,故它们的 加速度相等,均为α,设绳作用物体上 2 图2-5(c)
教案 第二章 牛顿定律 21 2 E R Gm g = 二 弹性力 当两物体相互接触而挤压时,它们要发生形变。物体形变时欲恢复原来的形状,物 体间会有作用力产生。这种物体因形变而产生欲使其恢复原来形状的力叫做弹性力。 常见的弹性力有:弹簧被拉伸或压缩时产生的弹簧弹性力;绳索被拉紧时所产生的 张力;重物放在支承面上产生的压力(作用在支承面上)和支持力(作用在物体上)等。 例题 1 质量为 m、长为 l 的柔软细绳,一端系着放在光滑 桌面上质量为 m的物体,如图 2-2(a)所示,在绳的另一 端加如图所示的 F。绳被拉紧时会略有伸长(形变),一般 伸长甚微,可略去不计。现设绳的长度不变,质量分布 是均匀的。求:(1)绳作用在物体上的力;(2)绳上任意点的张力。 解 如图 2-2(b)所示,设想在绳索上点 P 将绳索分为 两段,它们之间有拉力 FT和 F T作用,这一对拉力称为张. 力.,它们的大小相等、方向相反。 (1)由题意知,绳和物体均被约束在如图(c)所示的 Ox 轴上运动,且绳的长度不变,故它们的 加速度相等,均为 a,设绳作用物体上 图 2-5(a) l m F m P FT FT 图 2-5(b) m FT0 a F m FT0 a 图 2-5(c) N F 图 2-4 弹性力示意图

教案第二章牛顿定律 的拉力为Fm,物体作用在绳端的力为F0,它们是作用力与反作用力,故Fm=一Fm 由牛顿第二定律,对物体与绳可分别有 Fto=m'a 和 F-F'To =ma 由于FD=Fo所以,物体与绳的加速度为 a- (1) m'+m 绳对物体的拉力为 从上式可以看出,由绳传递给物体的力F小于作用在绳另一端的外力F。只有当绳 的质量m远小于物体的质量m'时,绳的质量可忽略不计时,下才与F近似相等 ②由于绳的长度不变,且质量分布均匀,一 故其单位长度的质量即质量线密度为mM。在图 dx Fr dx Fr+dF ()中,取物体与绳连接处为原点O,在距原点 dm dm O为x的绳上,取一线元dx,其质量元为 图2-5(d) dr=mdv1。按图(d所示的示力图,由牛顿第二定律,有 (Fr+dFt)-F;=(ma="adx 利用式(1),上式为 mF dF(m'm 从图(c)有时,F=F,所以上式的积分为 ∫5d,= m'mifdx F 得 Fm 斤=F-m+m0-刊 化简,得 22
教案 第二章 牛顿定律 22 的拉力为 FT0,物体作用在绳端的力为 F T0,它们是作用力与反作用力,故 FT0=-F T0。 由牛顿第二定律,对物体与绳可分别有 FTO = m a 和 F − F TO = ma 由于 FT0=FT0 所以,物体与绳的加速度为 m m F a + = (1) 绳对物体的拉力为 F m m m F + TO = 从上式可以看出,由绳传递给物体的力 FT0 小于作用在绳另一端的外力 F。只有当绳 的质量 m 远小于物体的质量 m 时,绳的质量可忽略不计时,FT0 才与 F 近似相等。 (2)由于绳的长度不变,且质量分布均匀, 故其单位长度的质量即质量线密度为 m/l。在图 (d)中,取物体与绳连接处为原点 O,在距原点 O 为 x 的绳上,取一线元 dx,其质量元为 dx=mdx/l。按图(d)所示的示力图,由牛顿第二定律,有 ( ) a x l m FT + dFT − FT = (dm)a = d 利用式(1),上式为 x m m l mF F d ( ) d T + = 从图(c)有 x=l 时,FT=F,所以上式的积分为 + = F x F r x m m l mF F T 0 d ( ) d 得 ( ) ( ) T l x l m m Fm F F − + = − 化简,得 l dx dm FT dx FT+dFT dm 图 2-5(d)