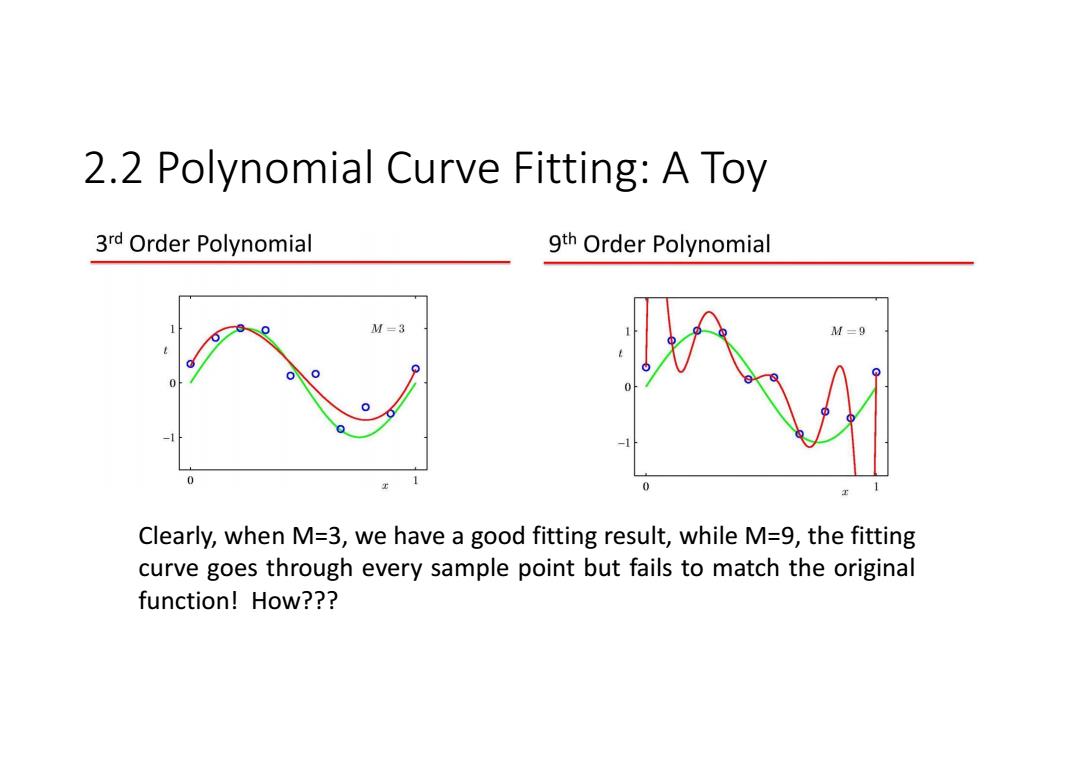
2.2 Polynomial Curve Fitting:A Toy 3rd Order Polynomial 9th Order Polynomial M=3 M=9 Clearly,when M=3,we have a good fitting result,while M=9,the fitting curve goes through every sample point but fails to match the original function!How??
2.2 Polynomial Curve Fitting: A Toy Clearly, when M=3, we have a good fitting result, while M=9, the fitting curve goes through every sample point but fails to match the original function! How???

2.2 Polynomial Curve Fitting:A Toy We need to finda w that minimizes the fitting error,when M=9,the xi t1 equation set W= actually have a solution! xiol t10 x灯 1,x1,x7,,x9 it's actually a Vandermonde matrix,thus 1,10,x0,2x0 the determinant is),thus the equation has a 1≤i≤j≤10 unique solution which means there exists a w that eliminates the fitting error
2.2 Polynomial Curve Fitting: A Toy We need to find a w that minimizes the fitting error, when M=9, the equation set actually have a solution! , it’s actually a Vandermonde matrix, thus the determinant is , thus the equation has a unique solution which means there exists a that eliminates the fitting error

2.2 Polynomial Curve Fitting:A Toy Now let's jump back to the previous problem: When doeswtnn have a solution??? x 1,x1,x2,,xM Let's denote =X x1,N,x绿,…,x州 Then we have XTXw =>N=1tnxn X is a N X (M+1)Vandermonde matrix.Vandermonde matrix is a full rank matrix i.e.rank()=min(M +1,N)rank(X) While XTX is a (M+1)x(M+1)matrix. So when N >M 1,the above problem has a unique solution.Otherwise the equation has infinite solutions!
2.2 Polynomial Curve Fitting: A Toy Now let’s jump back to the previous problem: When does ே ் ୀଵ ே ୀଵ have a solution??? Let’s denote ଵ ் ் ଵ ଵ ଶ ଵ ଶ Then we have ் ே ୀଵ is a ) Vandermonde matrix. Vandermonde matrix is a full rank matrix i.e. ் While ் is a matrix. So when , the above problem has a unique solution. Otherwise the equation has infinite solutions!

2.2 Polynomial Curve Fitting:A Toy x好 Let's look at this equation: W= 网 WhenN M+1,it doesn't have a solution which means that no w can eliminate the fitting error,other wise the equation has solutions which means that there exists w that can eliminate the fitting error!
2.2 Polynomial Curve Fitting: A Toy Let’s look at this equation: When , it doesn’t have a solution which means that no w can eliminate the fitting error, other wise the equation has solutions which means that there exists w that can eliminate the fitting error!
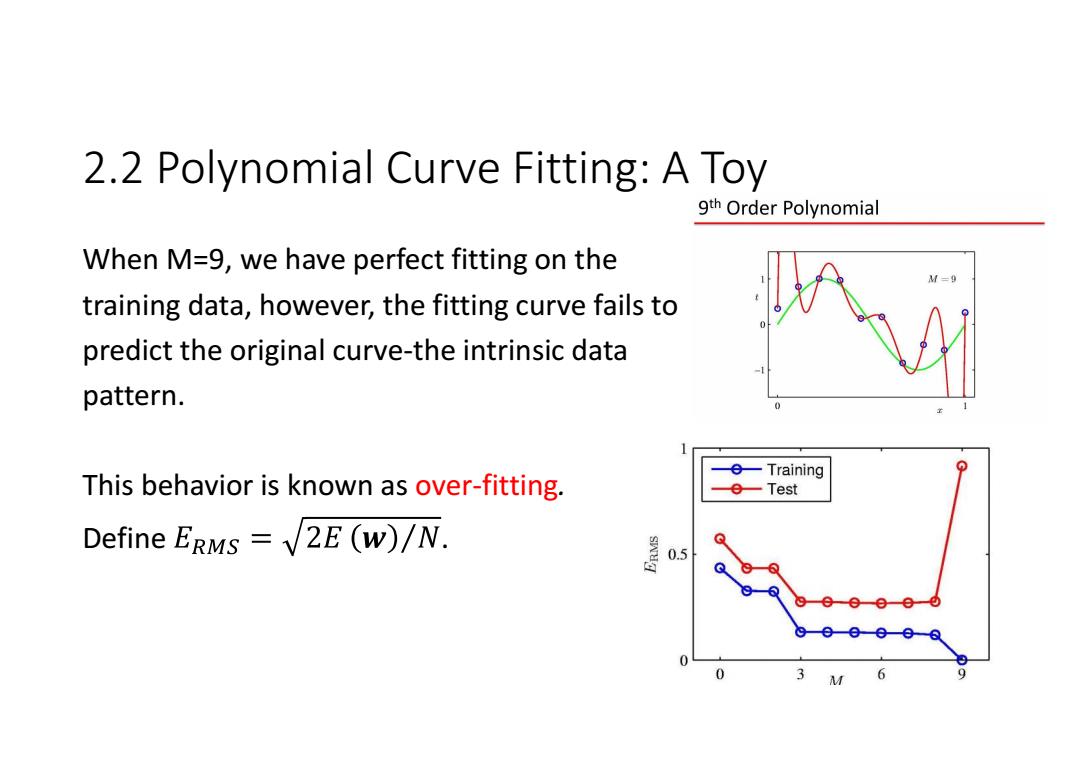
2.2 Polynomial Curve Fitting:A Toy 9th Order Polynomial When M=9,we have perfect fitting on the training data,however,the fitting curve fails to predict the original curve-the intrinsic data pattern. -e-Training This behavior is known as over-fitting. e一Test Define ERMs =2E (w)/N. 0.5 -0000 M 6
2.2 Polynomial Curve Fitting: A Toy When M=9, we have perfect fitting on the training data, however, the fitting curve fails to predict the original curve-the intrinsic data pattern. This behavior is known as over-fitting. Define