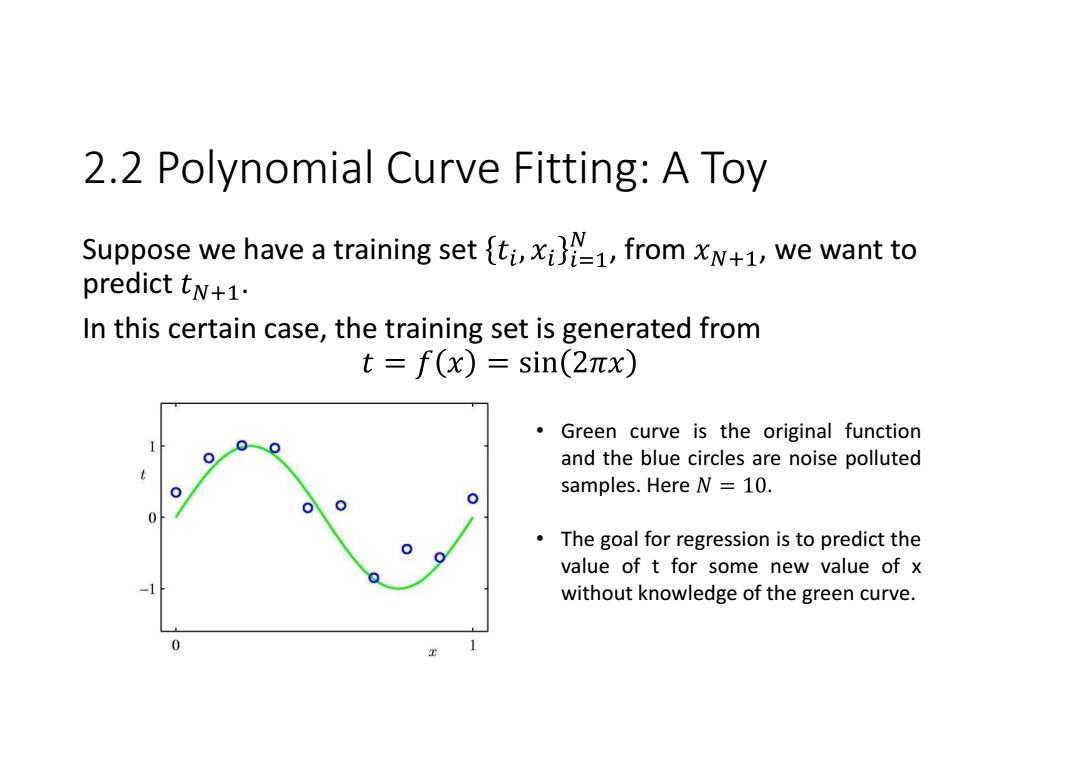
2.2 Polynomial Curve Fitting:A Toy Suppose we have a training set ti,,from xN+1,we want to predict tN+1. In this certain case,the training set is generated from t=f(x)=sin(2πx) 。 Green curve is the original function and the blue circles are noise polluted samples.Here N =10. The goal for regression is to predict the value of t for some new value of x without knowledge of the green curve
2.2 Polynomial Curve Fitting: A Toy Suppose we have a training set , from , we want to predict . In this certain case, the training set is generated from • Green curve is the original function and the blue circles are noise polluted samples. Here . • The goal for regression is to predict the value of t for some new value of x without knowledge of the green curve

2.2 Polynomial Curve Fitting:A Toy The prediction objective is intrinsically difficult in that we have to generalize from a finite and noise-corrupted data set. We have many approaches to deal with this regression,here for our teaching purpose,we adopt this linear polynomial model. ·Suppose,f(x,W)=w0+ω1x+ω2x2+..+WMxM where M is the order of the polynomial
2.2 Polynomial Curve Fitting: A Toy • The prediction objective is intrinsically difficult in that we have to generalize from a finite and noise-corrupted data set. • We have many approaches to deal with this regression, here for our teaching purpose, we adopt this linear polynomial model. • Suppose, where M is the order of the polynomial

2.2 Polynomial Curve Fitting:A Toy The values of the coefficients will be determined by fitting the polynomial to the training data. To do this,we can minimize an error function which measures the misfit between f(x,w)and the training set w.r.t w. A natural choice of error function is E0w)=2∑fw)-tn m=
2.2 Polynomial Curve Fitting: A Toy • The values of the coefficients will be determined by fitting the polynomial to the training data. • To do this, we can minimize an error function which measures the misfit between and the training set w.r.t . • A natural choice of error function is

2.2 Polynomial Curve Fitting:A Toy ·E(w)=2∑m1f(x,wW)-tn2=2∑m=1{x7w-tn2 where xn [1 xnx...xM] Further simplifications yield E(w)=2∑wrxw-2tw+ n=1 Setting the derivative of E(w)equal to 0,we have: ∑xnw=∑tnxn n=1 n=1 By solving this equation,we get the optimum w in least square sense
2.2 Polynomial Curve Fitting: A Toy • = where • Further simplifications yield • Setting the derivative of equal to 0, we have: • By solving this equation, we get the optimum w in least square sense
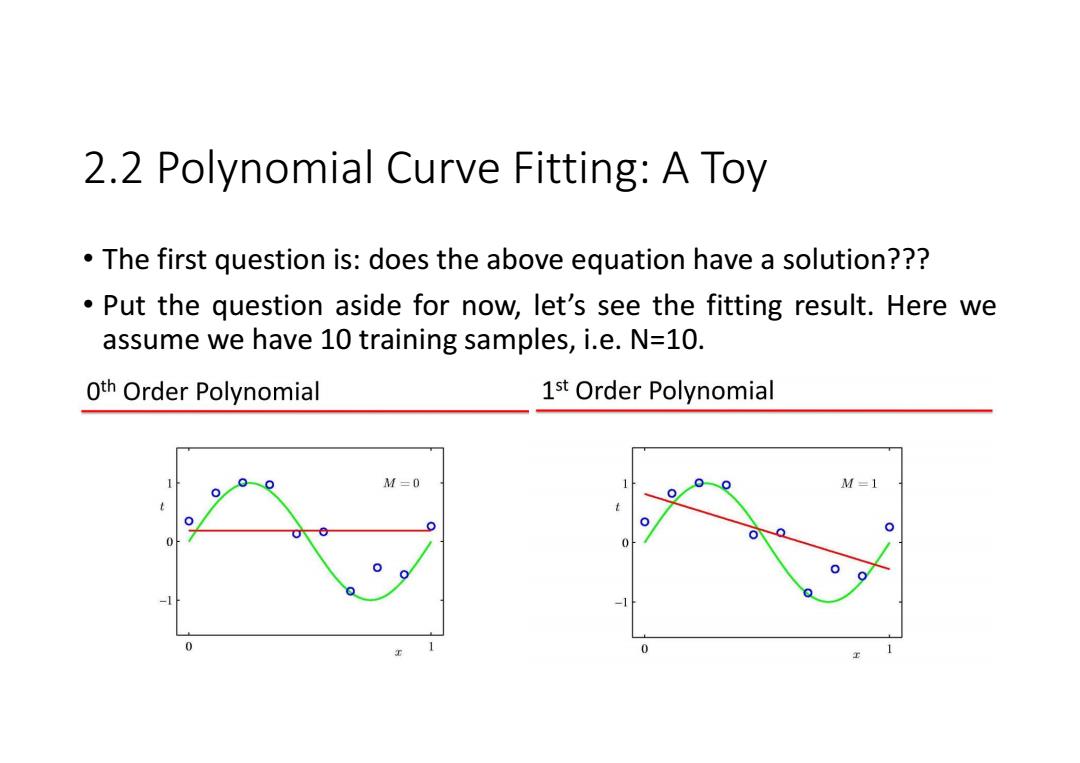
2.2 Polynomial Curve Fitting:A Toy The first question is:does the above equation have a solution??? Put the question aside for now,let's see the fitting result.Here we assume we have 10 training samples,i.e.N=10. Oth Order Polynomial 1st Order Polynomial M=0 M=1 0 0
2.2 Polynomial Curve Fitting: A Toy • The first question is: does the above equation have a solution??? • Put the question aside for now, let’s see the fitting result. Here we assume we have 10 training samples, i.e. N=10