2. 举例说阴组合 罗由路的 例4-1试分析 & 图4-1所示电路的逻 辑功能。 解:第一步: 由逻辑图可以写输 出F的逻辑表达式 为: 图4-1例4-1逻有电路图 F-(AB)(AC)(BC))
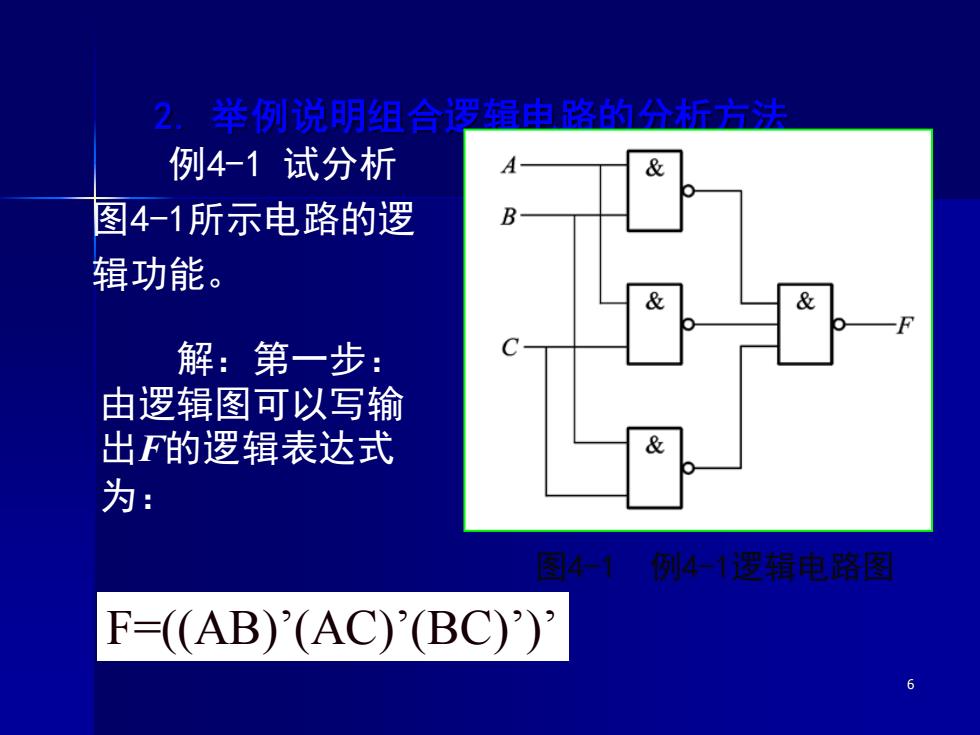
6 2. 举例说明组合逻辑电路的分析方法 例4-1 试分析 图4-1所示电路的逻 辑功能。 解:第一步: 由逻辑图可以写输 出F的逻辑表达式 为: 图4-1 例4-1逻辑电路图 F=((AB)’(AC)’(BC)’)’
第二步:可变换为 F=((AB)(AC)(BC)) F=AB+AC+BC 第三步:列出真值表如 表-1 例4-真值表 表4-1所示。 A B 第四步:确定电路的逻 0 0 0 辑功能。 由真值表可知,三个变 0 0 量输入A,B,C,只有两 个及两个以上变量取值为1 时,输出才为1。可见电路 可实现多数表决逻辑功能
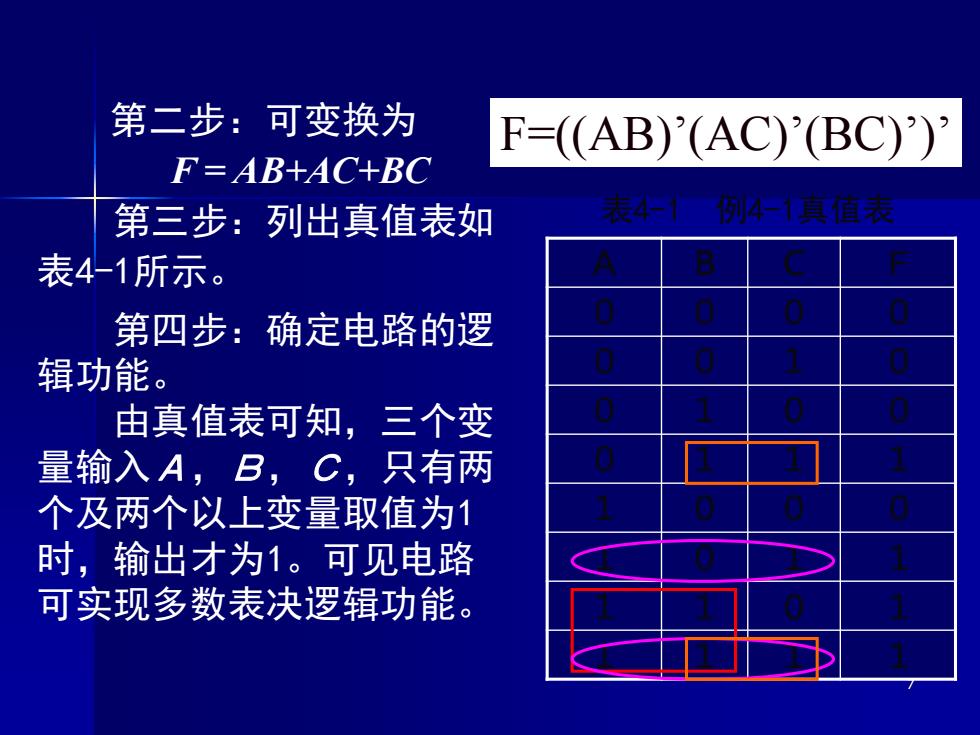
7 第二步:可变换为 F = AB+AC+BC 第三步:列出真值表如 表4-1所示。 A B C F 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 表4-1 例4-1真值表 第四步:确定电路的逻 辑功能。 由真值表可知,三个变 量输入A,B,C,只有两 个及两个以上变量取值为1 时,输出才为1。可见电路 可实现多数表决逻辑功能。 F=((AB)’(AC)’(BC)’)’
例4-2分析图4-2(a)所示电路的逻辑功能。 & 图42例42逻镇电路圆
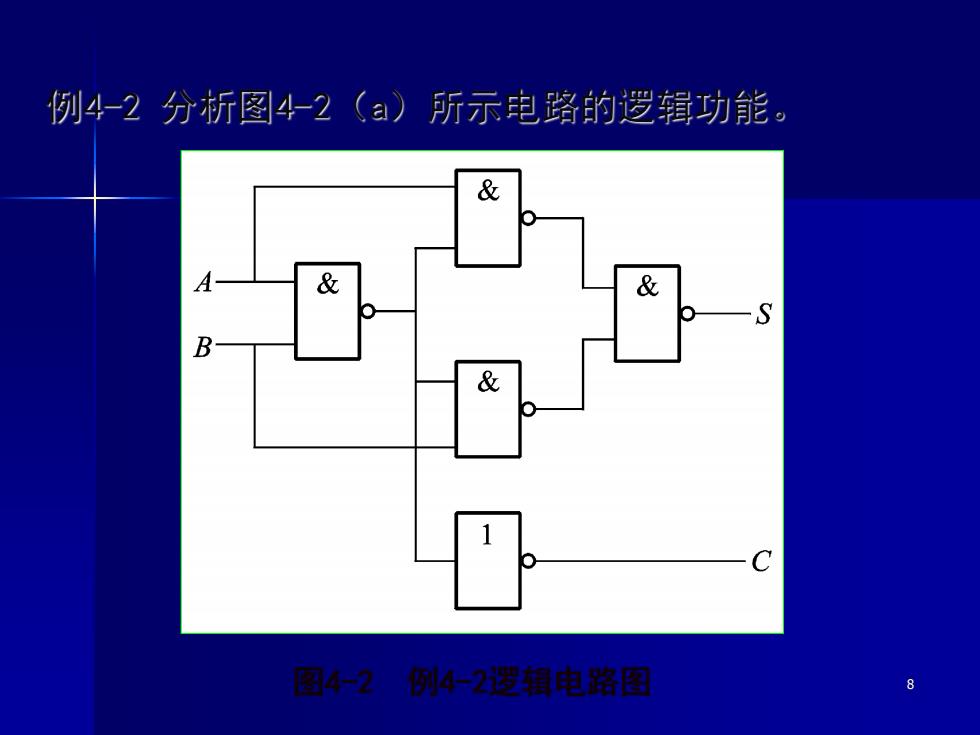
8 例4-2 分析图4-2(a)所示电路的逻辑功能。 图4-2 例4-2逻辑电路图
解:为了方便写表达式,在图中标注中间变 比如F、F和F3 S =(F2F3)” & =(AF)'(BF)' =(A(AB))'B(AB)')) =A(AB)'+B(AB)' =(A+B)(A+B) (a) =A'B+AB' C=万=AB=AB
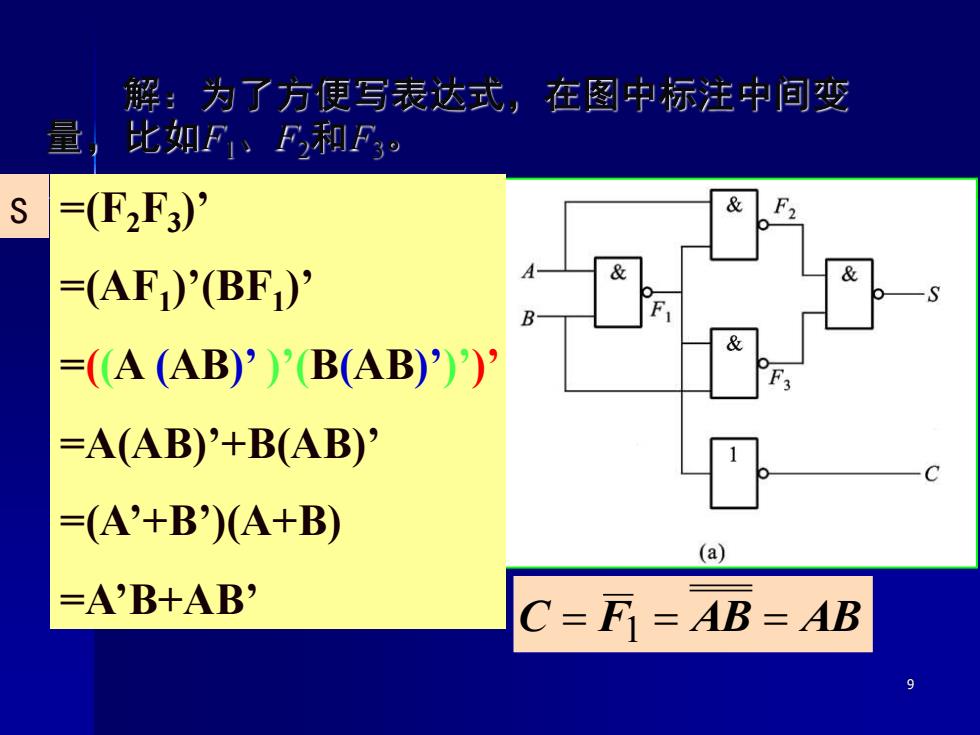
9 解:为了方便写表达式,在图中标注中间变 量,比如F1、F2和F3。 S C = F1 = AB = AB =(F2F3 )’ =(AF1 )’(BF1 )’ =((A (AB)’ )’(B(AB)’)’)’ =A(AB)’+B(AB)’ =(A’+B’)(A+B) =A’B+AB’
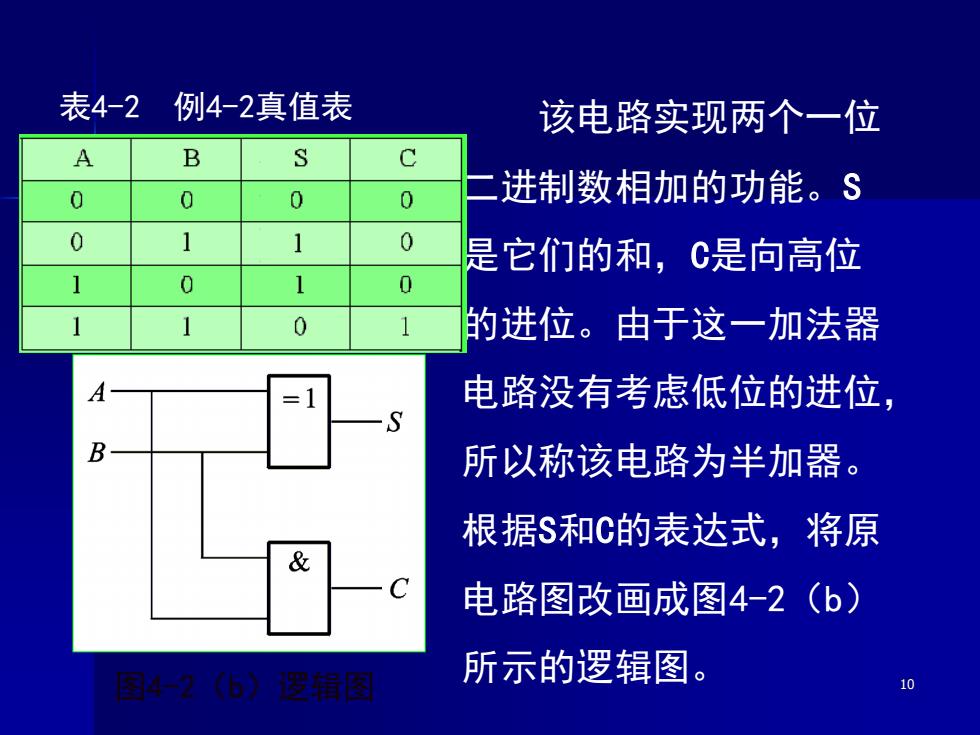
表4-2例4-2真值表 该电路实现两个一位 A B S C 0 0 0 0 进制数相加的功能。S 0 1 1 0 是它们的和,C是向高位 0 0 1 0 1 的进位。由于这一加法器 =1 电路没有考虑低位的进位, 所以称该电路为半加器。 根据$和C的表达式,将原 & 电路图改画成图4-2(6) 国4?6)遐用图 所示的逻辑图。 10
10 表4-2 例4-2真值表 该电路实现两个一位 二进制数相加的功能。S 是它们的和,C是向高位 的进位。由于这一加法器 电路没有考虑低位的进位, 所以称该电路为半加器。 根据S和C的表达式,将原 电路图改画成图4-2(b) 图4-2(b)逻辑图 所示的逻辑图