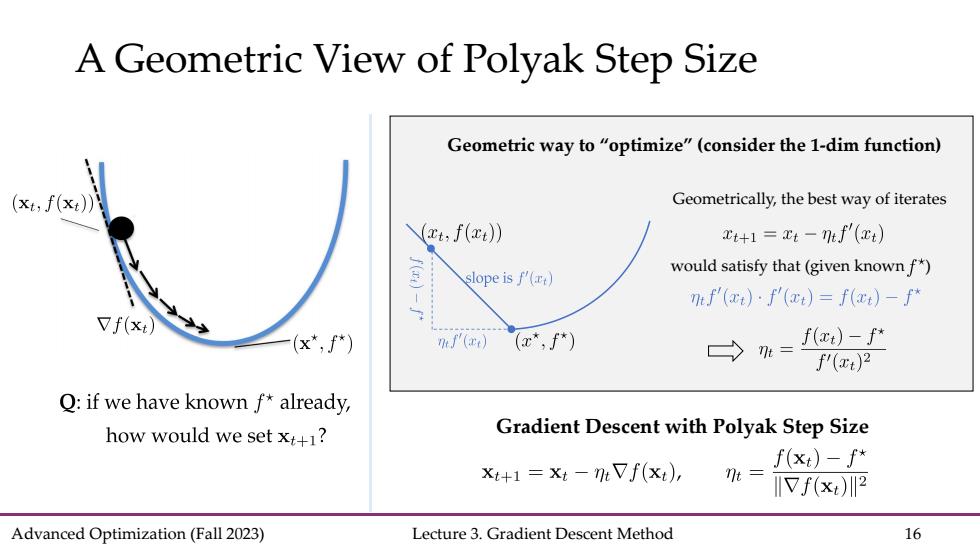
A Geometric View of Polyak Step Size Geometric way to"optimize"(consider the 1-dim function) (xt,fxt)月 Geometrically,the best way of iterates (zt,f(xi)) Ut+1=xt-mf'(xt) slope is f'() would satisfy that(given known f*) mf(xt).f(xt)=f(xt)-f* Vf(x:) (x*,f*) J() (x*,f) f(xt)-f* f'(c)2 Q:if we have known f*already, how would we set x:+1? Gradient Descent with Polyak Step Size X+1=xi-mVf(x), f(xt)-∫* 7t= IIVf(x)2 Advanced Optimization(Fall 2023) Lecture 3.Gradient Descent Method 16
Advanced Optimization (Fall 2023) Lecture 3. Gradient Descent Method 16 A Geometric View of Polyak Step Size Gradient Descent with Polyak Step Size Geometric way to “optimize” (consider the 1-dim function) Geometrically, the best way of iterates would satisfy that (given known )

Polyak Step Size 》 lIVf(), Vf(x)卡0 Polyak step size:n= 1 Vf(x:)=0 月:2g Boris Polyak (1835)passed away today.An immensely gentle person the waylknew him and a gant of scence in general and optimization in assume known f*for a moment. Darticulat His neme.results and legscy will lve forever. anoe,2015 (A tore T.Polyak y B T.Polak. INTRODUCTION OPTIMIZATION Introduction to optimization Boris T.Polyak Optimization Software,Inc.,1987 Boris T.Polyak 1935-2023 Advanced Optimization(Fall 2023) Lecture 3.Gradient Descent Method 17
Advanced Optimization (Fall 2023) Lecture 3. Gradient Descent Method 17 Polyak Step Size Boris T. Polyak 1935-2023 Introduction to optimization Boris T. Polyak Optimization Software, Inc., 1987