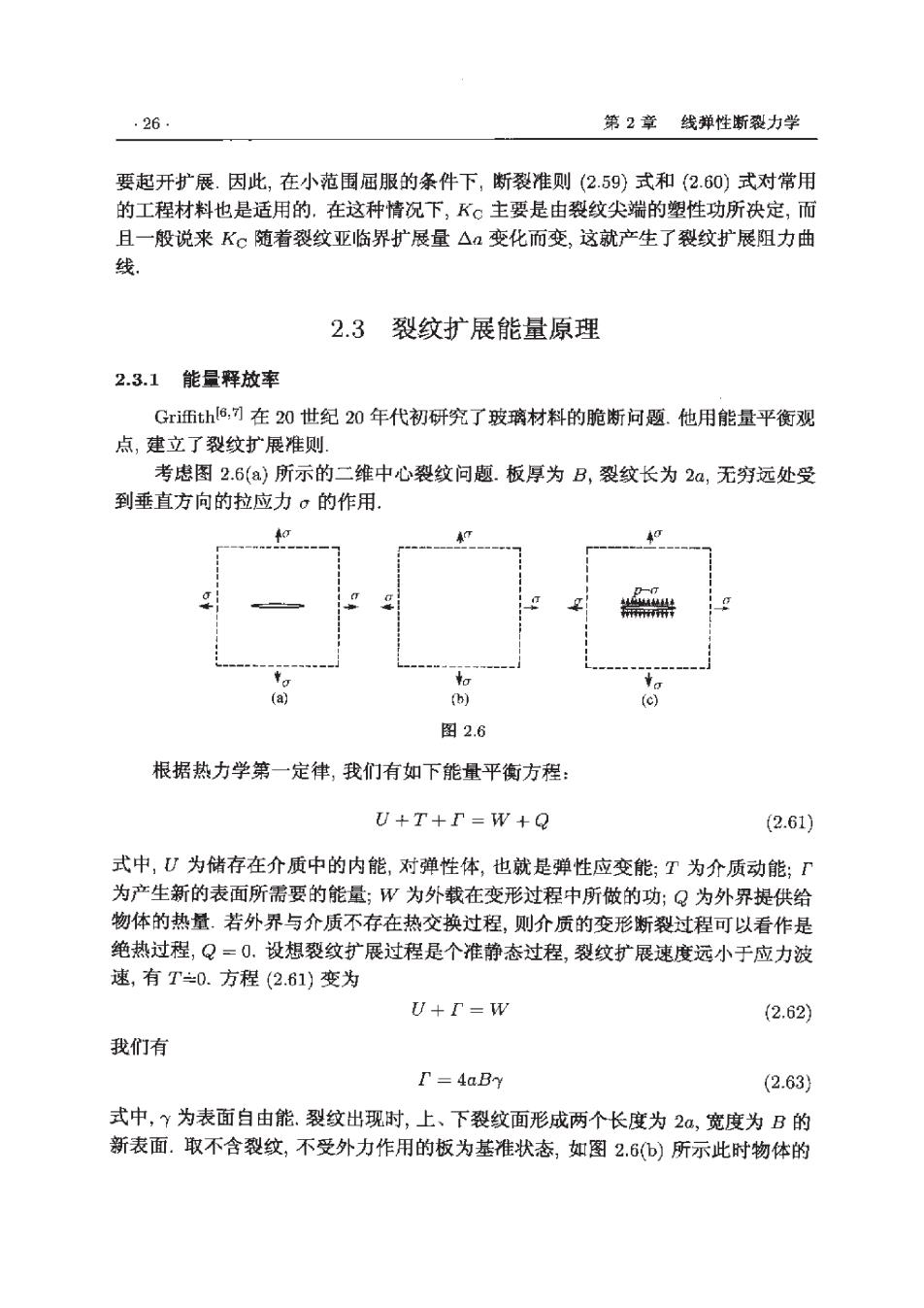
.26 第2章线弹性断裂力学 要起开扩展.因此,在小范围屈服的条件下,断裂准则(2.59)式和2.60)式对常用 的工程材料也是适用的,在这种情况下,Kc主要是由裂纹尖端的塑性功所决定,而 且一般说来Kc随着裂纹亚临界扩展量△变化而变,这就产生了裂纹扩展阻力曲 线。 2.3 裂纹扩展能量原理 2.3.1 能量释放率 Gri田th6,可在20世纪20年代初研究了玻璃材料的脆断问题.他用能量平衡观 点,建立了裂纹扩展准则 考虑图2.6(a)所示的二维中心裂纹问题.板厚为B,裂纹长为2a,无穷远处受 到垂直方向的拉应力。的作用 (a) 6) (c) 图2.6 根据热力学第一定律,我们有如下能量平衡方程: U+T+I=W+Q (2.61) 式中,U为储存在介质中的内能,对弹性体,也就是弹性应变能;T为介质动能;Γ 为产生新的表面所需要的能量;W为外载在变形过程中所做的功;Q为外界提供给 物体的热量.若外界与介质不存在热交换过程,则介质的变形断裂过程可以看作是 绝热过程,Q=0,设想裂纹扩展过程是个准静态过程,裂纹扩展速度远小于应力波 速,有T=0.方程(2.61)变为 U+r=W (2.62) 我们有 T=4aBy (2.63) 式中,Y为表面自由能.裂纹出现时,上、下裂纹面形成两个长度为2a,宽度为B的 新表面.取不含裂纹,不受外力作用的板为基准状态,如图2.6(b)所示此时物体的

2.3裂纹扩展能量原理 .27. 内能为零.如图2.6b)不含裂纹的板施加外载荷,外载均匀由小到大逐渐增加到σ, 此时外载所做的功W。恰好等于物体所储蓄的内能U0.然后割开长度为2a裂纹 但维持裂纹上、下表面的拉应力.如图2.6(c)所示在裂纹上、下表面施加一对压应 力,由小而大逐新增加到-,这样得到图2.6(a)所示的状态 在这个变形过程中,维持外加载荷不变.此时物体在变形增加过程中内能增量 为 PiduidS (2.64) 式中,S。是物体外表面S中,作用有外载部分;而Sm是物体内表面,也就是上、 下裂纹面.显然(2.64)式右端第1项即是外力功增量,而第2项可改写为 2 p.dundis--2B(a-p)dodr (2.65) 式中,卫是附加在袭纹面上的压应力.上式中的负号表明面力与位移增量d,方向 相反.由此得 du=dw -2B (a-p)dviz (2.66) 利用p与u之间的线性关系,不难得到① △(U-W)=-Ba v(x)dr (2.67) 式中,2(x)是压应力(-Q)作用下,裂纹面张开位移,参考文献「4,由线弹性力学 求解得 回=品+va2-g,以≤a (2.68) 将(2.68)式代入(2.67)式,积分后得 △U-Ww)=-+a2Ba2 2.69) 84 将2.69)式与(2.62)、(2.63)式比较,得 2y=+19g2a= g2元a 8地 E (2.70) 式中, E= 了E/1-2), 对平面应变 E. 对平面应力 ①△中表示图2.6(c)变形过程中物理量中的增量

.28 第2章线弹性断裂力学 (2.70)式确立了在裂纹扩展条件下,外加应力g与裂纹半长a之间的关系式,Griffith 的断裂判据为 2E'Y (2.71) 元 简要地说,我们有 0=o+△ (2.72) W=Wo+△W 式中,U。是无裂纹板在外裁作用下所储存的弹性应变能:W是对无裂纹板,外载 所做的功;△U是引!入长度为2a的裂纹后,板的弹性应变能的增加;△W是期间外 力所做的功.我们有 U-W=AU-△w=-o2Q2 B (2.73) Grth还发现,若将(2.71)式改写为 ocrVπa=v√2'7 (2.74) 则右端项与材料参数有关,而左端乃是临界应力与裂纹尺寸开根的乘积, 能量平衡方程(2.62)可改写为 -dΠ=dT=2ydA 式中,Ⅱ是系统的势能Ⅱ=U一W,dA是新增加的裂纹面.由上式导得 G=别-2 (2.75) 式中,物理参量G称为能量释放率.采用符号G是为了纪念Gr田th, 公式(2.75)比之于(2.73)有很大的普适性,它不仅适用于中心裂纹,而且适用 于其他裂纹,包括三维裂纹, 能量释放率G可看作是试图驱动裂纹扩展的原动力,故又称为裂纹扩展力.而 公式(2.75)的右端是与材料性能有关的参数.称为临界能量释放率G1。,又称为裂 纹扩展阻力 跪性断裂的能量判据为 G1≥G1c (2.76) 2.3.2能量释放率与应力强度因子关系 能量准则是一种全局性准则,而应力强度因子准则是一种局部准则,它们是两 种不同观点,但这两种推则存在内在联系 如图2.7所示,讨论1型二维单边裂纹
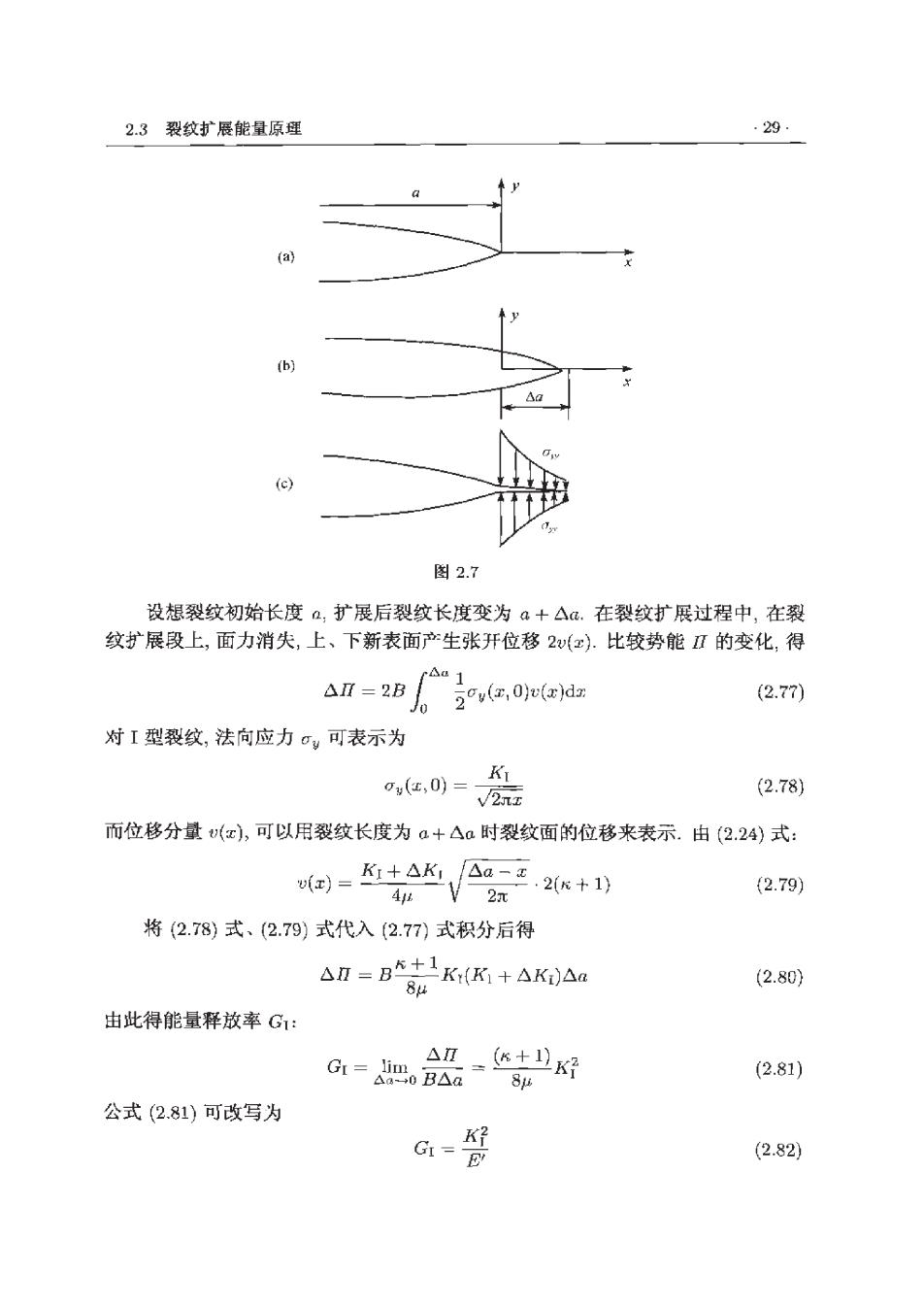
2.3裂纹扩展能量原理 .29. (a) 6 图2.7 设想裂纹初始长度a,扩展后裂纹长度变为a+△a.在裂纹扩展过程中,在裂 纹扩展段上,面力消失,上、下新表面产生张开位移2(z).比较势能Ⅱ的变化,得 △Ⅱ=2B Aa 1 20v(,0j2(x)dz (2.77) 对I型裂纹,法向应力σy可表示为 0y(c,0)= K V2ata (2.78) 而位移分量u(x),可以用裂纹长度为a+△a时裂纹面的位移来表示.由(2.24)式: 到=在+△k △a-E 46 .2(+1 (2.79) 2π 将(2.78)式、(2.79)式代入(2.77式积分后得 △n=B+1K,(K+△K△a (2.80) 84 由此得能量释放率G: △n=+业x好 Gi=ioB△a (2.81) 86 公式(2.81)可改写为 Gr= K (2.82)

·30 第2章线弹性断裂力学 此即能量释放率G1与应力强度因子K:之间的关系.由此看出当G达到临界值 GIC时,应力强度因子K1也达到临界值Krc: K E .=GIc (2.83) 所以能量释放率准则与应力强度因子淮则是等价的 对于Ⅱ型裂纹,如果假设裂纹也沿裂纹延长线扩展,那么同样有 C (2.84) 但是大量实验表明,纯Ⅱ型裂纹跪断,将以分岔形式扩展.分支裂纹与原裂纹延伸 线成65°~85°倾斜角,因此(2.84)式难以直接应用 对于纯Ⅱ型裂纹,实验表明裂纹沿其延长线扩展.类似的分析得 Gu K经1+叫 (2.85) 2.4裂纹尖端塑性区 对于绝大多数工程材料,裂纹尖端区域总是存在着一个塑性区.在小范围屈服 条件下,这个塑性区被周围的弹性区包围着,如果塑性区充分地小,那么周围的弹 性场依然可以用K场表征,我们可以用线弹性理论近似估算塑性区的形状和尺寸, 并对应力强度因子进行修正 2.4.1塑性区的形状和大小 先讨论I型裂纹.应力场c,0g和y可以用公式(2.17))表示。 考察平面应变问题,主应力的公式为 7{+±5V:2+ (2.86) 将(2.17)式代入(2.86)式,得 01 K cos 1+8in V2πT 2 02 K (2.87) C08 √2rr 2 K 03=0z= cos22) (2.88) V2π 采用Mises屈服准则,等效应力ag为