
.16 第2章 线弹性断裂力学 鉴于物体的应变能必须是有界的,因此λ必须大于零,由此: n=0,1,2 (2.12) 显然裂纹尖端的奇性应力场对应于入=分,此时有 D=-B,C=3A 相应的应力函数为 U(r,9)=Cx号 9.130 2 sin 2 +sin 38 (2.13) 令K1=CV2元,Kn=DV2玩. 考察I型裂纹,此时K1≠0,KⅡ=0.将(2.13)式代入(2.6)式,得 K Or= Av2ar 5c092 0 -co2 Ku 8 06= 3 cos +cw2 (2.14) 4v2元r K1 38 sin 4v2nr 十sim2 在裂纹前方,0=0 KI 0r=F8= Tr8=0 V2nr (2.15) 公式(2.15)表明,I型裂纹尖端前方,应力场具有一专奇异性.参数K1表征奇性场 强度,称为I型应力强度因子.应力强度因子概念的引入是断裂力学的突破性进展 近代断裂力学的迅猛发展的一个重要标志是对裂纹尖端应力场强有了深入而透彻 的了解。 对IⅡ型裂纹,则有 K 4V2π7 5 sin 2 39 +3sin -3KII 30 8= 4V2πr sin 2+sin 2 (2.16) Ku 4V2π1 2+3cos 30 2 类似的可以求得直角坐标系中应力分量:

2.1裂纹尖端弹性应力场 .17. I型: K1 3 0x= V2nr 2 KI 38 Oy= (2.17) V2nr K 30 sin V2nr 00s2c0 :=(o+w) 平面应变 0z=0 (2.18) Tr2=ty2=0, 平面应力 Ⅱ型: Ku sin 391 0x= 2[r Ku 30 0= sin V2πr 2 cos 2 cos (2.19) Ki 381 y= V2ir 2 1-sin 2i 2」 公式(2.18)对Ⅱ型裂纹依然成立. 2.1.2位移场 对平面应变问题,我们有 e:=0,02=v(ox+0w】 因此 方os-(ow+月 1-2「 所以 =g- (2.20) 类似地有 =g∫儿o-“小 (2.21) 将(2.18)式和(2.19)式代入(2.20)式和(2.21)式得
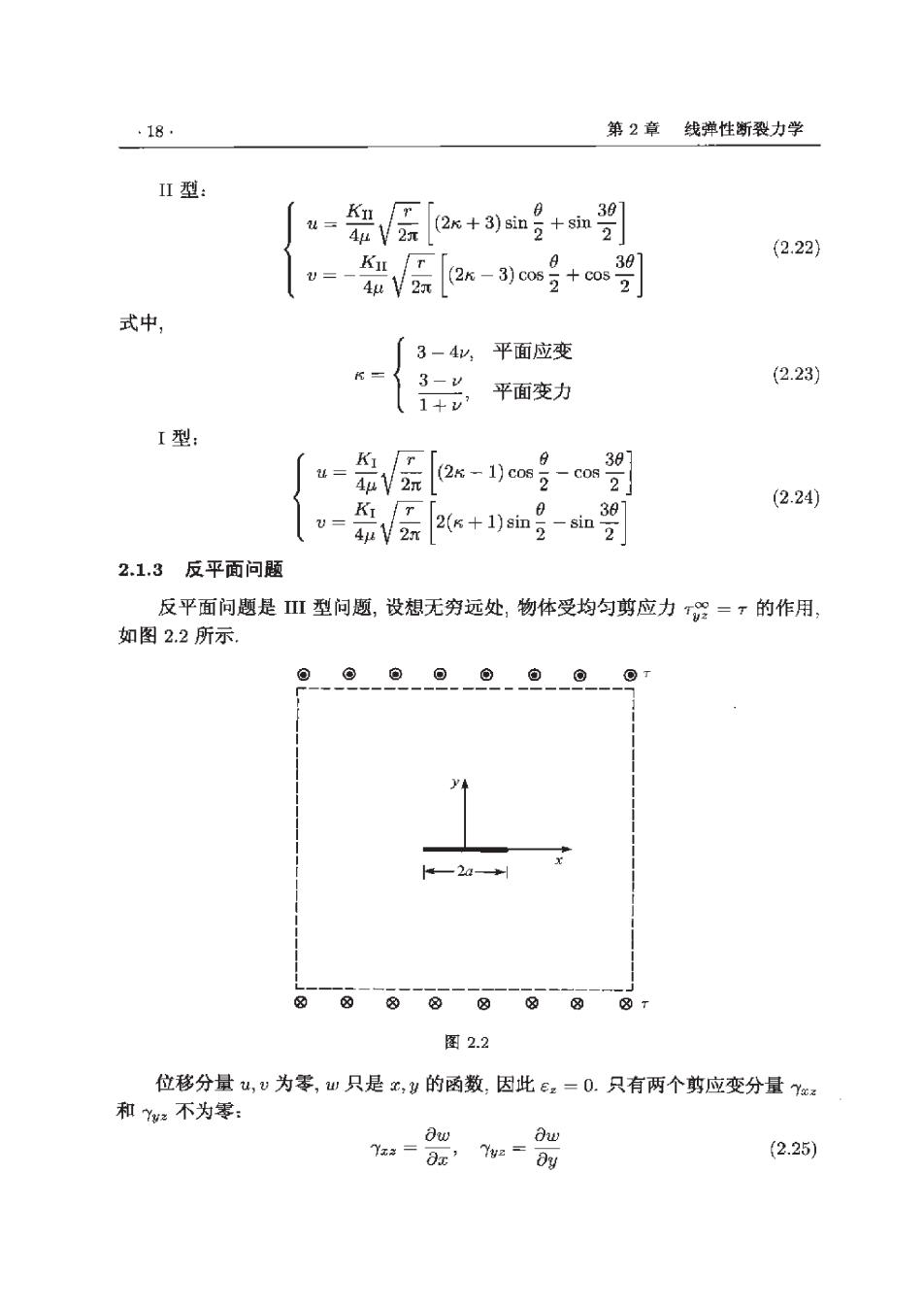
·18· 第2章 线弹性断裂力学 II型: Kn u= 4红V2元 (2x+3)sin2+si 2 (2.22) 38 =-4u 2 (2- 3)c062 +052】 式中, 3-4w, 平面应变 3-w (2.23) 1+ 平面变力 I型: = 3 4μ 2元 (2k-1)c0s 2 2] (2.24) V= 4uV2n 2(K+1)i加2 -sin 2 2.1.3反平面问题 反平面问题是型问题,设想无穷远处,物体受均匀剪应力=?的作用, 如图2.2所示 T —2a* 图2.2 位移分量u,v为零,w只是x,y的函数因此ez=0.只有两个剪应变分量Ycx 和Y%:不为零: ∂w Ow Yz=0' Yz= 8y (2.25)

2.1裂纹尖端弹性应力场 .19. 相应的应力分量为 8u (2.26) 8w Tu:=uyx=“ 平衡方程为 0r五十 rz=0 8x (2.27) by 将(2.26)式代入(2.27)式得 72w=0 (2.28) 区 w=r入fa(0) (2.29) 由方程(2.28)推出 f(0)=AsinλB+B cosA8 (2.30) 在裂纹面上,面力为零: T影x=0, 0=土元 (2.31) 注意到 = a( sin Ox Or 2cos0、1〔) r88 (2.32) 8() 18() sin+ c088 by r 00 将(2.29)式代入(2.26)式,得 Tss=uAr-1[Asin(-1)0+B cos(-1)0] Tu:=uAr-1[A cos(A-1)0-Bsin(A -1)0] (2.33) 将2.33)式代入(2.31)式得 Ac0s(A-1)π-Bsin(入-1)元=0 (2.34) Acos(入-1)r+B8in(A-1)元=0 由此得到如下特征方程: sin2元入=0 (2.35) 所以入=±受a=0,1以
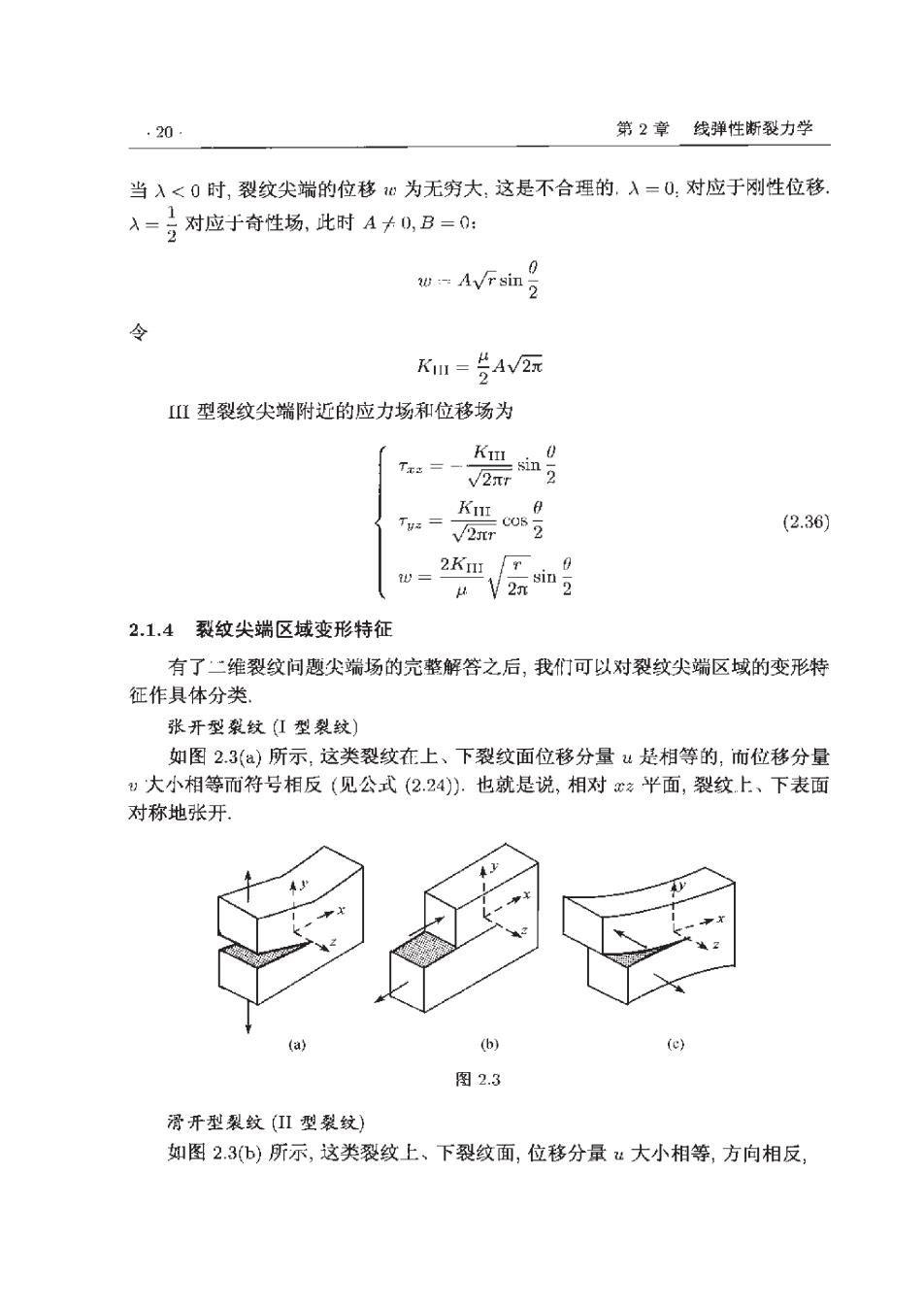
.20 第2章线弹性断裂力学 当入<0时,裂纹尖端的位移为无穷大,这是不合理的,入=0:对应于刚性位移 入=号对应于奇性场,此时A卡0,B=0: 0 w:Avr sin 令 KI=共AV2元 3 Ⅱ型裂纹尖端附近的应力场和位移场为 Tts=- Ku sin √2rr KII 8 V2nr (2.36) 2KII 0 sin 2 2n 2.1.4裂纹尖端区域变形特征 有了·二维裂纹问题尖端场的完整解答之后,我们可以对裂纹尖端区域的变形特 征作具体分类 张开型裂纹(红型裂纹) 如图2.3(a)所示,这类裂纹在上、下裂纹面位移分量是相等的,而位移分量 )大小相等而符号相反(见公式(2.24)).也就是说,相对之平面,裂纹上、下表面 对称地张开 (a) (b) (c) 图2.3 滑开型裂纹(I1型裂纹) 如图23(b)所示,这类裂纹上、下裂纹面,位移分量“大小相等,方向相反