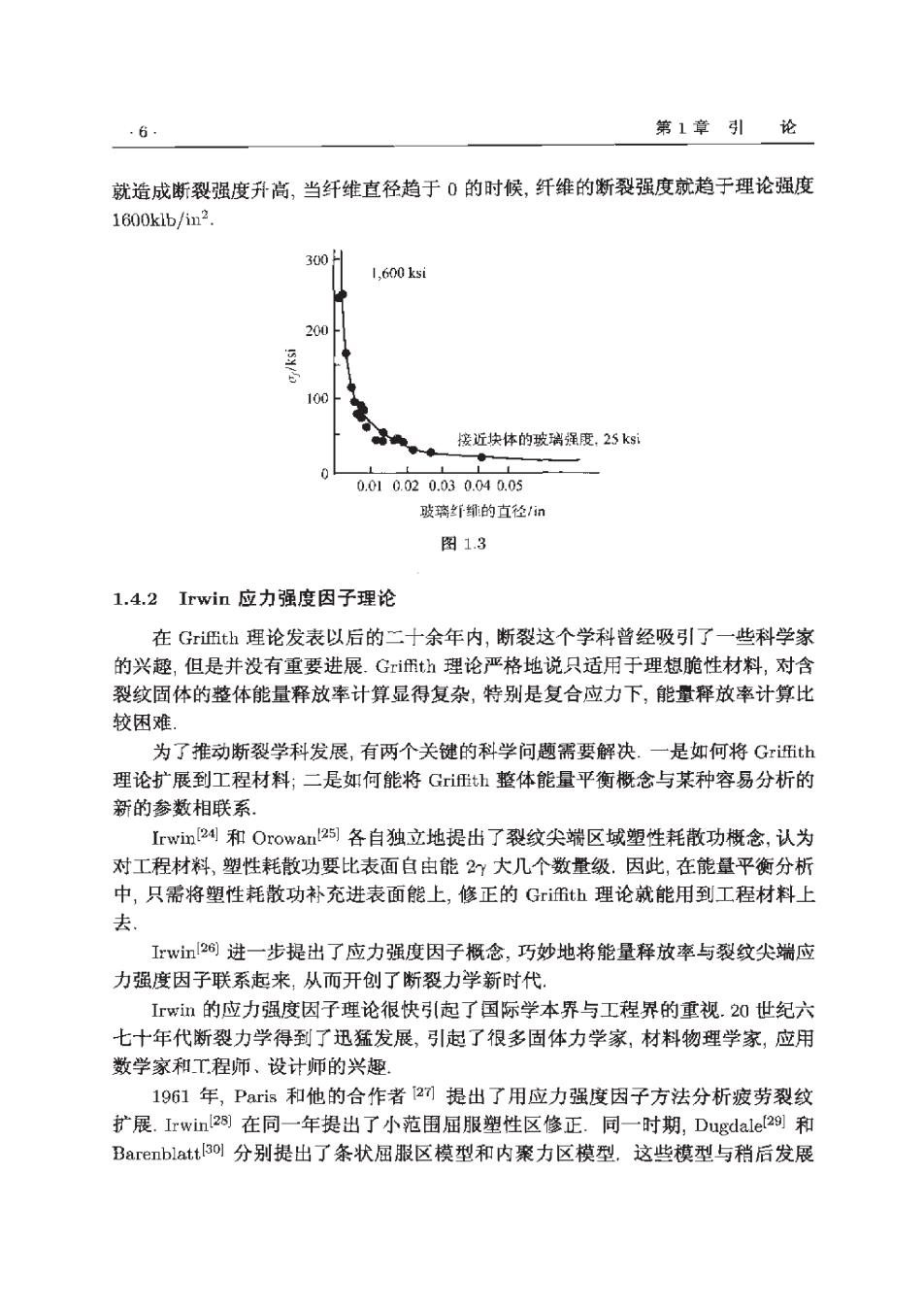
·6 第1章引 论 就造成断裂强度升高,当纤维直径趋于0的时候,纤维的断裂强度就趋于理论强度 1600klb/in2. 300 1.600ksi 200 100 接近块体的玻瑞强度,25ksi 0.010.020.030.040.05 玻璃的直径1in 图1.3 1.4.2Iwin应力强度因子理论 在Gith理论发表以后的二十余年内,断裂这个学科曾经吸引了一些科学家 的兴趣,但是并没有重要进展.Gi衎th理论严格地说只适用于理想脆性材料,对含 裂纹固体的整体能量释放率计算显得复杂,特别是复合应力下,能量释放率计算比 较困难 为了推动断裂学科发展,有两个关键的科学问题需要解决.一是如何将Gx田th 理论扩展到工程材料;二是如何能将Gi压th整体能量平衡概念与某种容易分析的 新的参数相联系 Irwin24和Orowan25]各自独立地提出了裂纹尖端区域塑性耗散功概念,认为 对工程材料,塑性耗散功要比表面自由能2大几个数量级.因此,在能量平衡分析 中,只需将塑性耗散功补充进表面能上,修正的Gth理论就能用到工程材料上 去 Irwi26)进一步提出了应力强度因子概念,巧妙地将能量释放率与裂纹尖端应 力强度因子联系起来,从而开创了断裂力学新时代 Irw的应力强度因子理论很快引起了国际学本界与工程界的重视.20世纪六 七十年代断裂力学得到了迅猛发展,引起了很多固体力学家,材料物理学家,应用 数学家和工程师、设计师的兴趣 1961年,Paris和他的合作者2可提出了用应力强度因子方法分析疲劳裂纹 扩展.1rwin2s]在同一年提出了小范围屈服塑性区修正.同一时期,Dugdale29和 Barenblatt3ol分别提出了条状屈服区模型和内聚力区模型,这些模型与稍后发展

1.4断毅力学起源与发展 。7。 起来的BCS位错连续分布模型3成为分析板材平面应力裂纹问题的理论基础, Wls32提出了以裂纹张开位移为断裂参量的COD方法,来分析含裂纹宽板的弹 塑性断裂问题 Liebowitzl3主编《断裂》七卷丛书和Sih34主编的《断裂力学》丛书(6卷) 的出版象征着断裂力学的辉煌.而l973年Tada、Paris和Irwin3汇编的第一本 应力强度因子手册问世,标志着线弹性断裂力学趋于成熟 1.4.3弹塑性断裂力学 l968年Ricel3l和Cherepanov[3提出了路径无关的J积分①,同年Hutchin son38、RiCe和Rosengron39建立了著名的HRR奇性场,为弹塑性断裂力学奠定 了重要的理论框架.这些学者都用全量理论描述材料的塑性本构关系,也就是用适 用于单调加载的非线性弹性理论来表征加载时裂纹顶端区域的塑性变形 后来发现J积分是Eshelby401951年建立的能量动量张量中的第-平移积分, 而能量动量张量又是与物理中Noether守恒积分紧密相关的[41) J积分不仅具有守恒性,而且与能量释放率G是相等的,这不仅使J积分具 有明确的物理意义,而且为能量释放率计算提供了有效的工具.在具体计算时,我 们可以用精度较高的远场来精确计算能量释放率】 HRR奇性场表征了弹塑性材料裂纹尖端应力应变场的主要特征,而】积分刻 画了HRR奇性场强度.1972年Begley和Landes42)基于块体试样的弹塑性断裂 实验,提出了以J积分为控制参量的弹塑性断裂准则.Rice,Paris和Merkle[43I进 步发展了J积分估算方法,从而为单试样测定J。提供了实用途径 J积分作为单参数断裂准则,在20世纪七八十年代曾经风行一时,独领风骚 十余年.但是精细的数值计算表明44,45裂纹顶端的应力应变场难以用HRR场表 征.大量的实验46,47证实,材料的断裂韧性C强烈地依赖试样几何和加截方式 中心裂纹试样测得的J1c要比弯曲试样测得的心高一个数量级 鉴于这种状况,1986年李尧臣和王自强[48建立了裂纹顶端弹塑性高阶场的基 本方程,得到平面应变的二阶场.证实了二阶场是本征场,它的幅值系数表征裂纹 尖端的三轴张力状态,这就为弹塑性断裂双参数断裂准则提供了理论基础 对于平面应变I型裂纹,夏霖和王自强[52,Xia、Waug和Shih53!得到了裂纹 尖端弹塑性应力应变场本征级数展开式前五项完整结果.Chao和Yang54,)得到 了高阶场前4项结果 Betegon和Hancock56指出了T应力的影响.Sharma和Aravasl57],O'Dowd 和Shih58!从不同角度分析了裂纹尖端场两项展开,证实了李尧臣和王自强[8!理 论分析的正确性.O'Dowd、Shih和Dodds59l进一步提出了JQ双参数断裂准则, ①俄文版原文发表在1967年

.8 第1章引论 魏悦广和王自强!基于裂纹尖端高阶场分析进一步证实裂纹尖端高阶场前5项 只含有3个独立参数,J,k2:4(或).提出以J和2为基础,4(或ks)为辅助参 量的J-k断裂准则.J-Q双参数断裂准则和☑-k断裂准则与Kk等6叫的实验符 合得相当好. 与J积分准则相平行的,裂纹张开位移准则(COD准则)在预测弹塑性材料 裂纹起始扩展方面也得到比较广泛的应用. 对于处于平面应力状态的薄板构件,如果材料是弹性理想塑性介质,那么COD 准则是与J积分准则等价的.但是对于常用的幂硬化材料,COD准则尚缺少坚实 的理论基础 Wels32根据大量实验于1965年提出了裂纹尖端开位移准则.Burdekin和 Stonel62!利用Dugdale模型得到裂纹尖端张开位移公式和标称应变之间关系曲线 但是这个理论预示曲线远远高于宽板的实验曲线.为此,Burdckin2提出如下经验 公式: e<0.5 Ey8 2Eysa -0.25, e>0.5 Eys 徐纪林和王自强阏提出了条状颈缩区模型.该模型设想裂纹尖端前方存在着 一个狭窄的条状颈缩区.在这个颈缩区上,法向正应力a=σu,04是薄板试样拉 伸曲线上的极限应力.颈缩区被周围的弹塑区所包围.采用这个模型,结合有限元 计算,徐纪林和王自强成功地从理论上预示了宽板实验曲线 J积分,COD单参数准则以及20世纪90年代发展起来的了-Q,J-k双参数准 测都是针对裂纹起始扩展提出来的 Hutchinson和Parislo4又将J积分作为控制参量,分析扩展裂纹,提出Jr阻 力曲线的思想.Pais等6引入了撕裂模量,以表征材料抵抗失稳扩展的能力 书展裂纹尖端场研究也是弹塑性断裂力学的重要内容.Chitaley和McClin- tock6)最先构造了理想塑性材料IⅡ型扩展裂纹尖端场.这个解答虽然比较简 单,却生动地揭示了扩展裂纹尖端场重要特征:裂尖附近的物质点在裂纹扩展过程 中经历了从加载到卸载再二次加截的复杂过程;而在裂纹延长线上,塑性应变出现 奇异性 理想塑性材料I型扩展裂纹尖端场,首先由Slepyanl677针对平面应变不可压 情况给出、Slepyan采用屈雷斯卡准则,新近场由四个角形区组成,在扇形区中应变 具有对数奇异性.Rice等68]和高玉臣[69得到了Mises屈服准则的渐近解

参考文献 9. 对平面应变可压缩情况,Drugan、Ric心和Sham[w与高玉臣四分别提出两个 不同的五区解,罗学富和黄克智[以;进一步改进了Druigan等人的结果 双线性硬化材料的扩展裂纹尖端场由Amazigo和Hutchinson3给出 以上讨论针对率无关材料.对于弹性幂硬化黏性材料,Hui和Riedel[4得到了 一个幂次型渐近场.这个场应力应变均具有r古奇异性,这个场仅适用于”>3 的情况.而且这个场是一个自治场,完全由材料的本构关系所决定,不包含任何与 外载及裂纹几问有关的参数 20世纪80年代以来,细观断裂力学和纳观断裂力学呈蓬勃发展趋势,这方面 的有关情况可参阅杨卫的著作《宏微观断裂力学》. 参考文献 []Broek D.Elementary engincering fracture mechanics.壬克,等译..【,程断裂力学基础. 北京:科学出版社,1980. [2]Shank M E.Brittle failure of steel structure:a brief listury.Metal progress,1954,66: 83-88. [3 Anderson W E.An engineering views brittle fracture history.Boeing rept.,1969. [4]Atallah S,U.S.history's worst LNG disaster.Firehouse,1979,1:29. [5 Kanninen M F.Popelar C H.Advanced fracture mcchanics.洪其麟,等译,高等断裂力 学.北京:北京航空学院出版社,1987 [6]Biggs W D.The brittle fracturc of steel.McDonald and Evans.1960. [7]Anderson T L.Fracture techanics,fundamentals and applications.Boca Raton:CRC Press,1991. [8]Duga JJ,Fisher W H.et al.The economic effecus of fracture in the United Statcs. NBS special publication 647-2,United States Dcpartement of Commerce,Washington, DC,1983,3. [9劳动部文件.关于开展锅炉和压力容器防爆技术研究的通知.1990. [10]BSI PD6493.Guidance on some methods for the derivation of acceptance levels for defects in fusion welded joiuts,1980,British Standard Institution;London,1980. [11]Harrison R P,Loosemore K,Mi I.Assessment of the integrity of structuzre containing defects.CEGB Report R/II/R6,London,CEGB,1976. [12]Kumar V,German M D,Shih CF.An engineering approach for elastic plastic fracture analysis.EPRI Report,EPRI,New York 1981,NP-1931. [13]Zahoor A.Ductile fracture Handbook.Novetech/EPRI,New York 1991,(1~3). [14]Failure and prevention:Vol.10 of Metals Handbook.ASM,Melals Park,OFI,1975. [15]Gdoutos EE.Fracture mechanics,an introduction.Kluwer Academic Publishes,1993. [16) Timoshenko S P.History of the strength of materials.New York:McGraw-Hill,1953

.10. 第1章引论 [17]Todhunter I;Pearson K.History of the theory of clasticity and the strength of materials. Cambridge:Cambridge University Press,1986. [18]Stanton T F,Batson R G.Proceedings of the Institute of Civil Engineering 211.1921: 67-100. [19]Docherty J G.Slow bending tests on largc notched bars.Engineering,1935,139: 211-213. [20]Irwin G R.Structurals aspects of brittle fracture.Applied Materials Research,1964,3: 65-81 21]Griffith AA.The phenomena of rupturc and flow in solids.Philosophical Trarsactions of the Royal Society of London A,1921,221:163-198. [22]Griffith AA.The theory of rupture.Proceedings of the First Cougress of Applied Mechanics,1924:55-63. [23]Inglis C E.Stresses in a plate due to the presence of cracks and sharp corners.Trans. Inst.Naval Arch.,1913,55:219-241. 24]Irwin G R.Fracture dynarics,in fracture of metals.Cleveland,Am.Soc.Metals,1948: 147-166. 25)Orowan E.Fracture and strength of solids.Reports on Progress in Physics,1948,XII: 185. [26]Irwin G R.Analysis of stress and strains ncar the end of a crack trausversing a platc. J.Applied Mechanics,1957,24:109-114. 27]Paris P C,Gomez M P,Anderson W P.A rational analytic theory of fatigue.The Trend in Engineering,1961,13:9-.14. 28]Irwin G R.Plastic zone near a crack and fracture toughness.Sagatore Research Cou- ference Proceedings,1961,4. [29]Dugdale D S.Yieldings in steel shects containing slits.J.Mech,Plys.Solids,1961,8: 100-104. [30]Barenblatt G I.The mathernatical theory of equilibrium cracks in brittie fracture.Ad- vances in Applied Mechanics,1962,VII:55-129. [31]Bilby B A,Cottrell A H,Swindeu K II.The spread of plastic yield from a notch.Proc, Roy.Soc.London,Ser,A,1963,272:304-314. [321 Wells AA.Unstable crack propagation in mctals:cleavage and fast fracture.Proceed- ings of the Crack Propagation Symposium,1961,1:84. [33]Liebowit H.Fracture:an advanced treatise,Vol.1-VII,New York:Academic,Press, 1968:1-VTI. [34]Sil G C.Mechanics of fracture.Leyden:Noordhoff International Publishing,1973-1979. (35]Tada H.Paris P C,Irwin G R.The Stress Analysis of Cracks Handbook.St.Louis: Paris Productions Inc.,1985