电子科技大学：《贝叶斯学习与随机矩阵及在无线通信中的应用 BI-RM-AWC》课程教学资源（课件讲稿）04 Asymptotic Spectrum Theorems（4/4）

4.6 Continuing Mapping Theorem The noise power: 交hn+L,n The interference and noise power can be written as: 2a,八[2a-j Thus,the SINR of MMSE is 11

11 4.6 Continuing Mapping Theorem 2 2 2 1 K H H k i i N k i            h h h I h  The noise power: The interference and noise power can be written as: 2 1 1 2 2 1 1 K K H H H H k i i N k k i i N k i i                              h h h I h h h h I h   Thus, the SINR of MMSE is

4.6 Continuing Mapping Theorem Thus,the SINR of MMSE is 2八 SINRMMSE 字+空j 2+8,, 1-交h+814 12

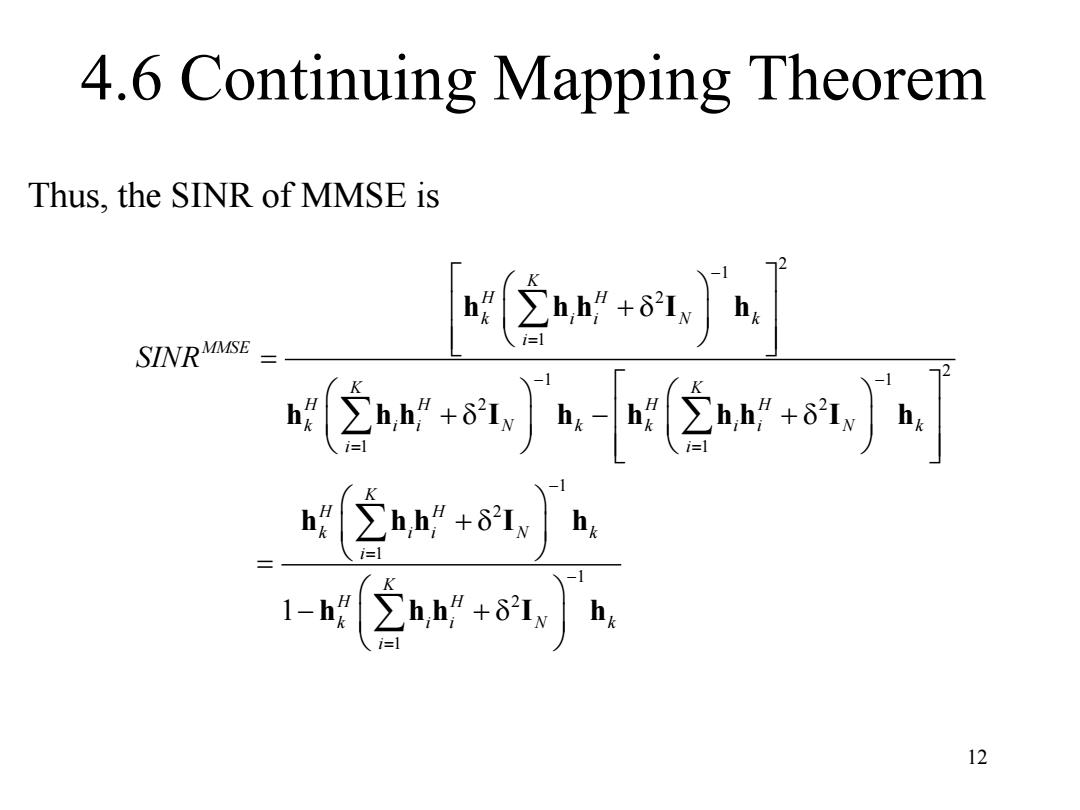
12 4.6 Continuing Mapping Theorem Thus, the SINR of MMSE is 2 1 2 1 2 1 1 2 2 1 1 1 2 1 1 2 1 1 K H H k i i N k i MMSE K K H H H H k i i N k k i i N k i i K H H k i i N k i K H H k i i N k i SINR                                                                            h h h I h h h h I h h h h I h h h h I h h h h I h