
专题选读5广义相对论概要
专题选读5 广义相对论概要
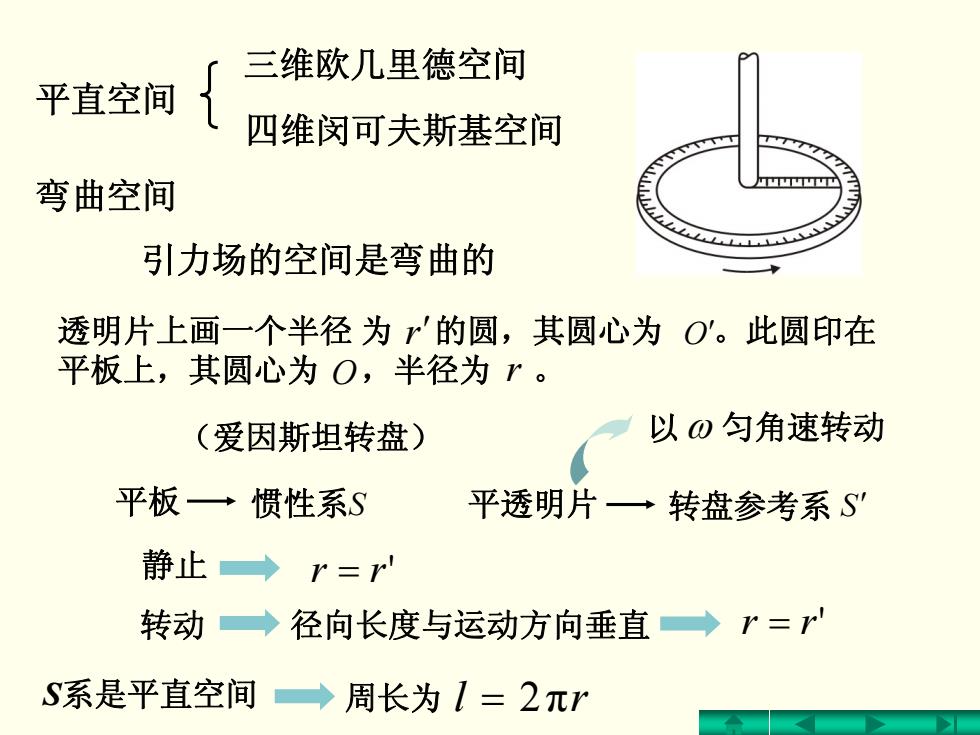
三维欧几里德空间 平直空间 四维闵可夫斯基空间 弯曲空间 引力场的空间是弯曲的 透明片上画一个半径为的圆,其圆心为O'。此圆印在 平板上,其圆心为O,半径为·。 (爱因斯坦转盘) 以0匀角速转动 平板一惯性系S 平透明片一 转盘参考系S 静止→r=r 转动◆径向长度与运动方向垂直→r= S系是平直空间→周长为1=2π
弯曲空间 平直空间 三维欧几里德空间 四维闵可夫斯基空间 引力场的空间是弯曲的 平板 惯性系S 平透明片 转盘参考系 S′ (爱因斯坦转盘) 以 ω 匀角速转动 透明片上画一个半径 为 的圆,其圆心为 。此圆印在 平板上,其圆心为 ,半径为 。 r ′ O′ O r 径向长度与运动方向垂直 r = r' 静止 r = r' 转动 S系是平直空间 周长为 l = 2πr

运动方向沿圆周 S系测的是动长 S系测的圆周静长1'=2πr(1- 022 >2元r 在S'系中圆周率>π 空间是弯曲的 S'系中存在惯性离心力,等效为径向引力,S'系观察者认为 产生空间弯曲的原因是引力 真空中光速是极限速率 两点间光经过的路径就是短程线 由光线的曲直可判断空间的曲直 惯性系中的短程线是直线 空间平直 非惯性系中的短程线是曲线 空间弯曲
运动方向沿圆周 S′系测的圆周静长 r c r 2πrl 2)1( π 2 1 2 22 ′ −= > ω − 在 系中圆周率 S′ > π 空间是弯曲的 S系测的是动长 S′系中存在惯性离心力,等效为径向引力, 系观察者认为 S′ 产生空间弯曲的原因是引力 真空中光速是极限速率 惯性系中的短程线是直线 空间平直 非惯性系中的短程线是曲线 空间弯曲 两点间光经过的路径就是短程线 由光线的曲直可判断空间的曲直 v a

黎曼空间 无引力的平直空间 有引力的弯曲空间 黎曼空间的主要特征 定义了空间中相邻两点之间距离ds ds是坐标变换不变量 在欧氏空间中 ds2 dx2+dy2+dz2 在闵氏空间中ds2=dx2+dy2+dz2-c2dt2 对弯曲的四维时空 ds2=gudx2+g2dx dx2 +gi3dx dx3 +gadx dxa +g2dx2dx+...+gdx
黎曼空间 有引力的弯曲空间 无引力的平直空间 黎曼空间的主要特征 定义了空间中相邻两点之间距离 ds ds 是坐标变换不变量 在欧氏空间中 在闵氏空间中 2 2 2 2 ds = dx + dy + dz 2 2 2 2 2 2 ds = dx + dy + dz − c dt 对弯曲的四维时空 2 21 2 1 44 4 12 1 2 13 1 3 14 1 4 2 11 1 2 d d d d d d d d d d d g x x g x s g x g x x g x x g x x + + + = + + + K

811 812 813 814 ds2=(dx dx2 dx3 dxa) 821 822 823 824 831 832 833 834 dx; 841 842 843 844 dxa 8 度规张量 8uv是对称张量 二次型ds2=gdx"dx" guv=8vu 欧氏空间 100 8w= 010 10 001 00 r2sin20 ds2 dr2 +r2d02+r2 sin2 ao
( ) ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 4 3 2 1 44434241 34333231 24232221 14131211 4321 2 d d d d d d d dd x x x x gggg gggg gggg gggg xxxxs μν g 度规张量 二次型 νμ μν ddd xxgs2 = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 100 010 001 gμν ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = θ μν 22 2 sin00 0 0 001 r rg 欧氏空间 2222222 θ ++= rrrs dsinddd ϕθ μν νμ = gg μν g 是对称张量