
5.2数字基养信号传输及其频谱特性 西安电子科技大学 通信工程学院ISN 5、2.2基带信号的频谱特性 目的:(1)确定数字基带信号的带宽 (2)确定序列中是否有位定时分量fs=1/Ts 假设g1(t)表示“0"码,g2(t)表示“1"码。 假设序列中任 一码元时间T内g1(t)和g2(t)出现的概率分别为P和1-P,且出 现是统计独立的,则随机序列$(t)可表示成 1=一o0 其中 g1(t-nTs),以概率P出现 g2(t-nTs),以概率(1-P)出现 通信原理2011年
西安电子科技大学 通信工程学院ISN 通信原理 2011年 5.2.2基带信号的频谱特性 目的:(1)确定数字基带信号的带宽 (2)确定序列中是否有位定时分量fs=1/Ts 假设g1(t)表示“0”码,g2(t)表示“1”码。 假设序列中任 一码元时间T内g1(t)和g2(t)出现的概率分别为P和1-P,且出 现是统计独立的,则随机序列s(t)可表示成 其中 () () n n st s t ∞ =−∞ = ∑ − − − = ( ),以概率 出现 以概率 出现 (1 ) ( ), ( ) 2 1 g t nT P g t nT P s t S S n 5.2数字基带信号传输及其频谱特性
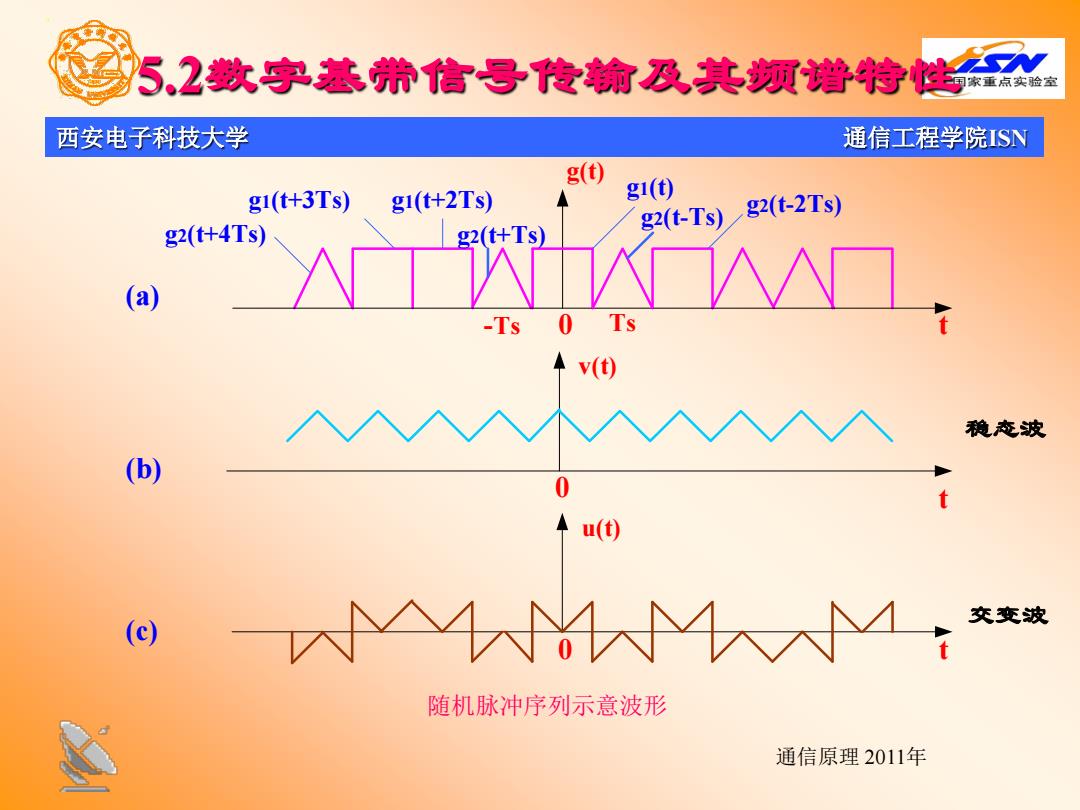
5,2数字基养信号传输及其频增特性 西安电子科技大学 通信工程学院SN g(t) g1(t+3Ts) g1(+2Ts) g1() g2(t+4Ts) g2(t-Ts)g2(t-2Ts) g2(t+Ts) (a) Ts 稳态波 (b) 0 ◆u(t) (c) △MM方 交变波 随机脉冲序列示意波形 通信原理2011年
西安电子科技大学 通信工程学院ISN 通信原理 2011年 5.2数字基带信号传输及其频谱特性 g(t) g1(t) g2(t-Ts) g2(t+Ts) g2(t-2Ts) g2(t+4Ts) g1(t+3Ts) g1(t+2Ts) -Ts 0 Ts t (a) v(t) t 0 (b) 随机脉冲序列示意波形 u(t) 0 t (c) 稳态波 交变波

5.2数字基带信号传输及其频增符性 西安电子科技大学 通信工程学院SN 我们可以把s(t)分解成稳态波v(t)和交变波u(t)。稳态波 是随机序列s(t)的统计平均分量,交变波是s(t)与ⅴ(t)之差。 v(t)和u(t)可分别表示成: 0=∑[Pgt-nI,)+1-P)8,-nI,】=∑.0 u(t)=s(t)-v(t) 其中第n个码元为 u,(t)=s,(t)-v,(t) 通信原理2011年
西安电子科技大学 通信工程学院ISN 通信原理 2011年 我们可以把s(t)分解成稳态波v(t)和交变波u(t)。稳态波 是随机序列s(t)的统计平均分量,交变波是s(t)与v(t)之差。 v(t)和u(t)可分别表示成: 其中第n个码元为 u (t) s (t) v (t) n = n − n 5.2数字基带信号传输及其频谱特性 1 2 ( ) [ ( ) (1 ) ( )] ( ) s s n n n v t Pg t nT P g t nT v t ∞ ∞ =−∞ =−∞ = − +− − = ∑ ∑ ut st vt () () () = −

5,2数字基养信号传输及其领增特性必 西安电子科技大学 通信工程学院SN 于是 0=∑4,(0 其中,un(t)可表示为 un (t)=an[g (t-nTs)-82(t-nTs)] 其中 通信原理2011年
西安电子科技大学 通信工程学院ISN 通信原理 2011年 5.2数字基带信号传输及其频谱特性 于是 其中, 可表示为 其中 − − − = , (1 ) 1 , P P P P an 以概率 以概率 1 2 ( ) [ ( ) ( )] nn s s u t a g t nT g t nT = −−− () () n n ut u t ∞ =−∞ = ∑ ( ) n u t

52数字基带信号传输及其频增符性 西安电子科技大学 通信工程学院ISN 1.v()的功率谱密度P(f) 由于V()是以T、为周期的周期信号,故 v(t)=>[Pg (t-nT,)+(1-P)82(t-nT.)] 可以展成傅氏级数 00 0=∑( 1m=-o0 式中 C.=月0esd 通信原理2011年
西安电子科技大学 通信工程学院ISN 通信原理 2011年 1.v(t)的功率谱密度 由于v(t)是以Ts为周期的周期信号,故 可以展成傅氏级数 式中 ( ) P f v ∑ ∞ =−∞ = − + − − n s nTs v(t) [Pg (t nT ) (1 P)g (t )] 1 2 ∫− − = 2 2 2 ( ) 1 s s S T T j m f t s m v t e dt T C π 5.2数字基带信号传输及其频谱特性 2 ( ) S j mf t m m vt Ce π ∞ =−∞ = ∑