
整理后: mx(t)+cx(t)+kx()=-mx() 式中一求相当于由地震产生的作用于结构上的 强迫力。 x0+e0+人0=-,0 wg月on-0 这是一个二阶线性非齐次微分方程,其解为齐次 方程的通解与非齐次方程通解之和。 11
11 mx t cx t kx t m t ( ) ( ) ( ) ( ) + + = − xg −mxg 2 ( ) ( ) ( ) ( ) ( ) 2 ( ) ( ) ( ) 2 + + = − + + = − g g c k x t x t x t x t m m c k k x t x t x t x t km m m 式中 相当于由地震产生的作用于结构上的 强迫力。 整理后: 2 ( ) ( ) ( ) ( ) ( ) 2 ( ) ( ) ( ) 2 + + = − + + = − g g c k x t x t x t x t m m c k k x t x t x t x t km m m ζ ω 这是一个二阶线性非齐次微分方程,其解为齐次 方程的通解与非齐次方程通解之和

2、关于单自由度振动的几个概念 圆频率 周期 频率 阻尼比 一 般结构的阻尼比0.010.1之间,一般取0.05
12 2、关于单自由度振动的几个概念 圆频率 周期 频率 阻尼比 一般结构的阻尼比0.01~0.1之间,一般取0.05。 2 1 2 2 k m T f T c c km m = = = = =

非齐次微分方程的解为齐次方程的通解与 非齐次方程的特解之和。 3、齐次方程的通解(有阻尼自由振动) x(t)+25ox(t)+o2x(t)=0 解为e)=eK0 co't+0)+5o0sino' o'=V1-52o 为有阻尼的圆频率 当很小时 ≈⑦ 注意其解与结构的初位移和初速度有关
13 3、齐次方程的通解(有阻尼自由振动) 当 很小时 2 x t x t x t ( ) 2 ( ) ( ) 0 + + = 2 (0) (0) ( ) [ (0)cos ' sin ' ] ' ' 1 t x x x t e x t t − + = + = − ' 解为 为有阻尼的圆频率 注意其解与结构的初位移和初速度有关。 非齐次微分方程的解为齐次方程的通解与 非齐次方程的特解之和
x(t)+25o.x(t)+ox(t)=0 齐次方程的通解 x(t)=e®Ix(0)coso't+ x(0)+S0x(0) sin@'t] (0 无阻尼自由振动 名三0 ℃=0.05有阻尼自由振动 ×<0) ℃=0.2
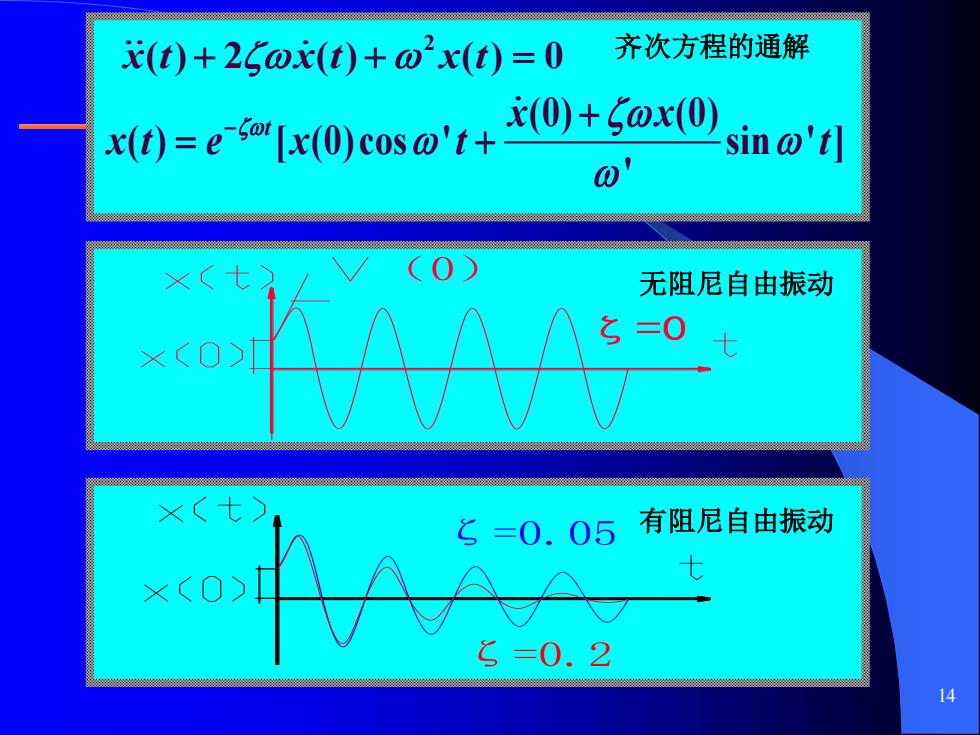
14 有阻尼自由振动 ζ=0 (0) 无阻尼自由振动 2 (0) (0) ( ) [ (0)cos ' sin ' 1 ' ] ' t x x x t e x t t − + = − = + 齐次方程的通解 ζ=0.2 ζ=0.05 2 x t x t x t ( ) 2 ( ) ( ) 0 + + =

4、非其次方程的特解 非齐次方程的特解— 杜哈米积分 x+250x+o2x=-x 思路: 1、利用齐次方程的通解 2、将地震的地面加速度分成有限个脉冲 3、讨论在单一脉冲作用后结构的响应 4、单一脉冲作用后结构的响应为自由振动,解的形 式已知(只是初速度不同)。 5、在所有脉冲作用下结构的响应为每一自由振动的 叠加(积分》
15 4、非其次方程的特解 2 2 g x x x x + + = − 非齐次方程的特解——杜哈米积分 思路: 1、利用齐次方程的通解 2、将地震的地面加速度分成有限个脉冲 3、讨论在单一脉冲作用后结构的响应 4、单一脉冲作用后结构的响应为自由振动,解的形 式已知(只是初速度不同)。 5、在所有脉冲作用下结构的响应为每一自由振动的 叠加(积分)