
大纲 口基本流程 口划分选择(特征选择) ▣剪枝处理 口连续与缺失值 口多变量决策树
大纲 p 基本流程 p 划分选择(特征选择) p 剪枝处理 p 连续与缺失值 p 多变量决策树

划分选择 口决策树学习的关键在于如何选择最优划分属性。一般而言,随着 划分过程不断进行,我们希望决策树的分支结点所包含的样本尽可 能属于同一类别,即结点的"纯度”(purity)越来越高 口经典的属性划分方法: ·基尼指数(CART) ●信息增益(ID3) ● 增益率(C4.5)
划分选择 p 决策树学习的关键在于如何选择最优划分属性。一般而言,随着 划分过程不断进行,我们希望决策树的分支结点所包含的样本尽可 能属于同一类别,即结点的“纯度”(purity)越来越高 p 经典的属性划分方法: l 基尼指数(CART) l 信息增益(ID3) l 增益率(C4.5)
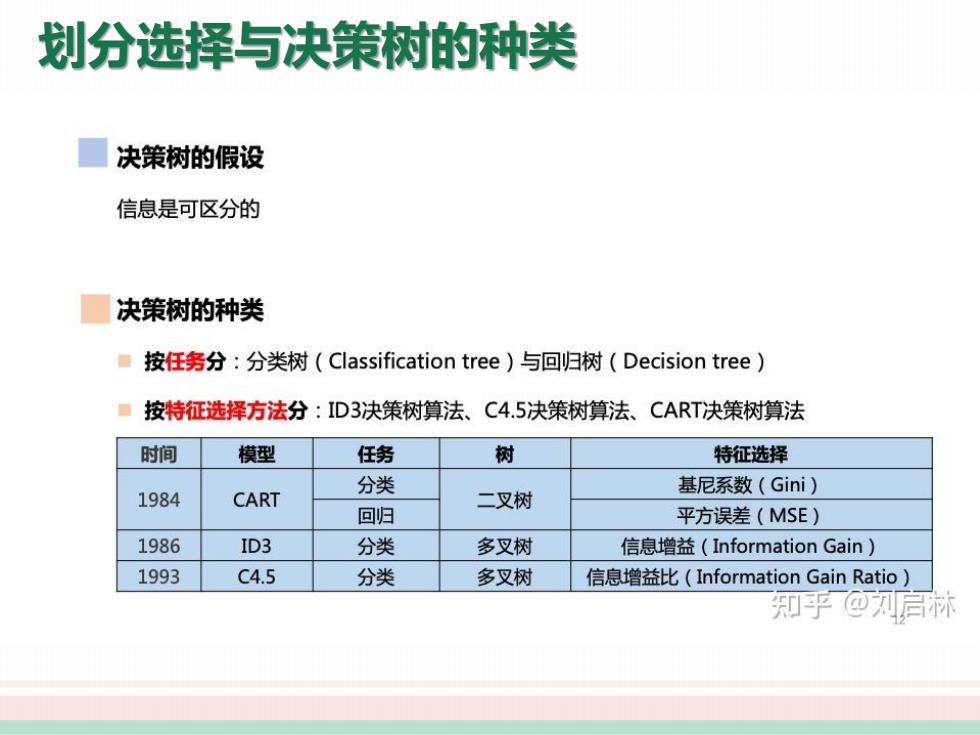
划分选择与决策树的种类 决策树的假设 信息是可区分的 决策树的种类 ■按任务分:分类树(Classification tree)与回归树(Decision tree) ■按特征选择方法分:ID3决策树算法、C4.5决策树算法、CART决策树算法 时间 模型 任务 树 特征选择 基尼系数(Gini) 1984 CART 分类 二叉树 回归 平方误差(MSE) 1986 ID3 分类 多叉树 信息增益(Information Gain) 1993 C4.5 分类 多叉树 信息增益比(Information Gain Ratio) 知乎@刘启林
划分选择与决策树的种类 p 数据集 的纯度可用“基尼值”来度量 越小,数据集 的纯度越高 p 属性 的基尼指数定义为: p 应选择那个使划分后基尼指数最小的属性作为最优划分属性,即 p CART [Breiman et al., 1984]采用“基尼指数”来选择划分属性 反映了从 中随机抽 取两个样本,其类别 标记不一致的概率

划分选择-信息增益红D3 口“信息熵”是度量样本集合纯度最常用的一种指标,假定当前样 本集合D中第类样本所占的比例为P(K=1,2,,1门),则D的信 息熵定义为 10川 Ent(D)=- p&log2 PR k=1 Ent(D)的值越小,则D的纯度越高 ▣计算信息熵时约定:若p=0,则plog2p=0 口Ent(D)的最小值为0,最大值为log2Dy
划分选择-信息增益ID3 p “信息熵”是度量样本集合纯度最常用的一种指标,假定当前样 本集合 中第 类样本所占的比例为 ,则 的信 息熵定义为 的值越小,则 的纯度越高 p 计算信息熵时约定:若 ,则 p 的最小值为 ,最大值为

划分选择-信息增益缸D3 ▣离散属性a有V个可能的取值{a,a a'}.,用a来进行划分,.则 会产生V个分支结点,其中第个分支结点包含了D中所有在属性 上取值为a"的样本,记为D"。则可计算出用属性a对样本集D进行 划分所获得的“"信息增益”: Gain(D,a)=Ent(D)- Ent(D) 1 为分支结点权重,样本数越 多的分支结点的影响越大 一般而言,信息增益越大,则意味着使用属性α来进行划分所获 得的“纯度提升”越大 口ID3决策树学习算法[QuinIan,1986]以信息增益为准则来选择划分 属性
划分选择-信息增益ID3 p 离散属性 有 个可能的取值 ,用 来进行划分,则 会产生 个分支结点,其中第 个分支结点包含了 中所有在属性 上取值为 的样本,记为 。则可计算出用属性 对样本集 进行 划分所获得的“信息增益”: p 一般而言,信息增益越大,则意味着使用属性 来进行划分所获 得的“纯度提升”越大 p ID3决策树学习算法[Quinlan, 1986]以信息增益为准则来选择划分 属性 为分支结点权重,样本数越 多的分支结点的影响越大