表1-2-1不同进位记数制对照表 十进制 二进制 十六进制 十进制 二进制 十六进制 0 0000 0 8 1000 8 0001 1 9 1001 9 2 0010 2 10 1010 A 3 0011 3 11 1011 B 4 0100 4 12 1100 C 5 0101 5 13 1101 D 6 0110 6 14 1110 E 1 0111 7 15 1111 F
表 1-2-1 不同进位记数制对照表 十进制 二进制 十六进制 十进制 二进制 十六进制 0 0000 0 8 1000 8 1 0001 1 9 1001 9 2 0010 2 10 1010 A 3 0011 3 11 1011 B 4 0100 4 12 1100 C 5 0101 5 13 1101 D 6 0110 6 14 1110 E 7 0111 7 15 1111 F

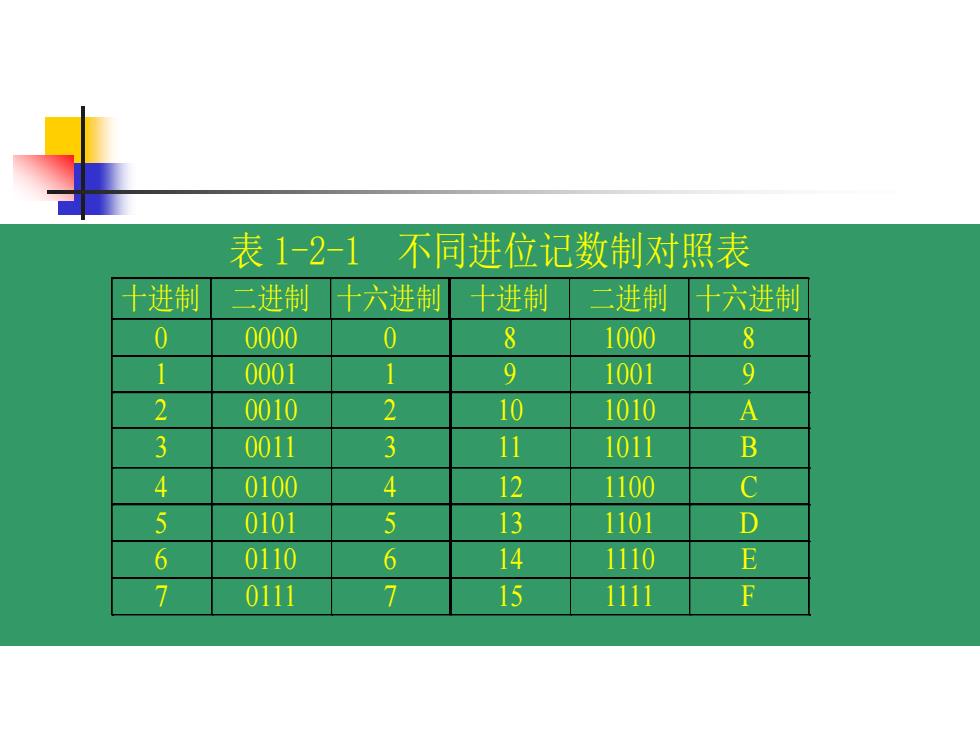
1.3.2进位计数制 一、十进制 符号集:0~9规则:逢十进一。 例:1234.5=1×103+2×102+3×101+4×100+5×10-1 加权展开式以10称为基数,各位系数为0~9。 一般表达式: dn-1×10m1+dn-2×10m-2+.+d0×100+d1×101+
一、十进制ND 符号集:0~9 规则:逢十进一。 例:1234.5=1×103 +2×102 +3×101 +4×100 +5×10-1 加权展开式以10称为基数,各位系数为0~9。 一般表达式: ND= dn-1×10n-1+dn-2×10n-2 +.+d0×100 +d-1×10-1+. 1.3.2 进位计数制

二、三进制N 符号集:0、1规则:逢二进一。 例:1101.101=1×23+1×22+0×21+1×20+1×21+1×23 加权展开式以2为基数,各位系数为0、1。 一般表达式: NB=b-1X2m-1+bn-2X2n-2+.+b0X20+b-1X21+
二、二进制NB 符号集:0、1 规则:逢二进一。 例:1101.101=1×2 3+1×2 2+0×2 1+1×2 0+1×2 -1+1×2 -3 加权展开式以2为基数,各位系数为0、1。 一般表达式: NB = bn-1×2 n-1 + bn-2×2 n-2 +.+b0×2 0 +b-1×2 -1+

三、士六进制Ng 符号集:0~9、A~F规则:逢十六进一。 例:DFC.8=13×162+15×161+12×160+8×161 展开式以十六为基数,各位系数为0~9,A~F。 一般表达式: Nhn-1×16m-1+hn-2×16m-2+.+h0×160+h-1×16 1十
三、十六进制NH 符号集:0~9、A~F 规则:逢十六进一。 例:DFC.8=13×162 +15×161 +12×160 +8×16-1 展开式以十六为基数,各位系数为0~9,A~F。 一般表达式: NH = hn-1×16n-1+ hn-2×16n-2+.+ h0×160+ h-1×16- 1+