
高等数学川课程教学大纲 (Advanced Mathematics II) 一、课程基本信息 课程编号:10062303-4 课程举别,七业基础理 农科类本科各专业 分:7 总学时:112,其中理论学时:112,实验学时:0 先修课程:无 后续课程:无 课程简介 本课程系统介绍一元函数的极限、连续、导数、微分及其应用、不定积分、定积分及其应用 微分方程及其应用:行列式、矩阵的基本运算、向量组线性相关性的理论、线性方程组的解的理论 和求解方法:概率论的基本概念、事件概率的多种求法、随机变量及其分布的理论、随机变量的数 字特征的求值方法。 主要教学方法与手段: 以讲授为主,辅之以多媒体教学、习题课和课外辅导,注重理论联系实际。 选用教材: 刘金林.高等数学(经济管理类)(第4版)[W].北京:机械工业出版社,2013: 陈建华线性代数(第4版)[).北京:机械工业出版社,2016: 宗序平概率论与数理统计(第3版)[].北京:机械工业出版社,2011: 必读书目: 选读书目: [1]杨棋喻主编.高等数学Ⅱ[.北京:高等教有出版社,2010: 「21王玉民杜晓林主编.高等数学「0.北京:中国农业出版社,2013: [3】张良云主编.线性代数 (第3版)[M.北京 高等教育出版社,2010: [4同济大学数学系编.线性代数(第5版)[M.北京:高等教有出版社,2007 [5]张国权刘金山主编.应用概率统计M.北京:中国农业出版社,2015: [6]盛骤谢式千潘承毅主编.概率论与数理统计(第5版)[W.北京:高等教育出版 计.010. [7)][美]Morris K1ine著.古今数学思想(英文版,1-3).上海:上海科技出版社,2014 [8]A history of mathematics:an introduction Victor Katz Addison-esley, 19982nded: 二、课程总目标 本课程是高等学校农科类本科各专业必修的重要基础课。通过本课程的学习,使学生对高等数 学、线性代数、概率论的基本概念、基本理论、基本方法有比较系统的认识,构建较为宽广的知识 结构。逐步培养学生抽象概 问题的能力 定的逻辑推理能力、比较熟练的运算能力和自学能力 提高学生在数学方面的素质和修养,培养学生综合运用所学知识分析问愿、解决问题的能力,学会 运用本课程提供的数学思想、数学方法解决简单的应用问题,激发学生的探素与创新意识,为学习 其它基础课程和专业课程打下基础。 三、课程教学内容与教学要求
1 高等数学 II 课程教学大纲 (Advanced Mathematics II) 一、课程基本信息 课程编号:10062303-4 课程类别:专业基础课 适用专业:农科类本科各专业 学 分:7 总 学 时:112, 其中理论学时:112, 实验学时:0 先修课程:无 后续课程:无 课程简介: 本课程系统介绍一元函数的极限、连续、导数、微分及其应用、不定积分、定积分及其应用、 微分方程及其应用;行列式、矩阵的基本运算、向量组线性相关性的理论、线性方程组的解的理论 和求解方法;概率论的基本概念、事件概率的多种求法、随机变量及其分布的理论、随机变量的数 字特征的求值方法。 主要教学方法与手段: 以讲授为主,辅之以多媒体教学、习题课和课外辅导,注重理论联系实际。 选用教材: 刘金林.高等数学(经济管理类)(第 4 版)[M].北京:机械工业出版社,2013; 陈建华.线性代数(第 4 版)[M].北京:机械工业出版社,2016; 宗序平.概率论与数理统计(第 3 版)[M].北京:机械工业出版社,2011; 必读书目: 无 选读书目: [1] 杨棋喻主编.高等数学Ⅱ[M].北京:高等教育出版社,2010; [2] 王玉民 杜晓林主编.高等数学[M].北京:中国农业出版社,2013; [3] 张良云主编.线性代数(第 3 版)[M].北京:高等教育出版社,2010; [4] 同济大学数学系编.线性代数(第 5 版)[M].北京:高等教育出版社,2007; [5] 张国权 刘金山主编.应用概率统计[M].北京:中国农业出版社,2015; [6] 盛骤 谢式千 潘承毅主编.概率论与数理统计(第 5 版)[M].北京:高等教育出版 社,2010; [7] [美] Morris Kline 著.古今数学思想(英文版,1-3)[M].上海:上海科技出版社,2014; [8] A history of mathematics : an introduction Victor J. Katz Addison-Wesley, 1998 2nd ed ; 二、课程总目标 本课程是高等学校农科类本科各专业必修的重要基础课。通过本课程的学习,使学生对高等数 学、线性代数、概率论的基本概念、基本理论、基本方法有比较系统的认识,构建较为宽广的知识 结构。逐步培养学生抽象概括问题的能力、一定的逻辑推理能力、比较熟练的运算能力和自学能力, 提高学生在数学方面的素质和修养,培养学生综合运用所学知识分析问题、解决问题的能力,学会 运用本课程提供的数学思想、数学方法解决简单的应用问题,激发学生的探索与创新意识,为学习 其它基础课程和专业课程打下基础。 三、课程教学内容与教学要求
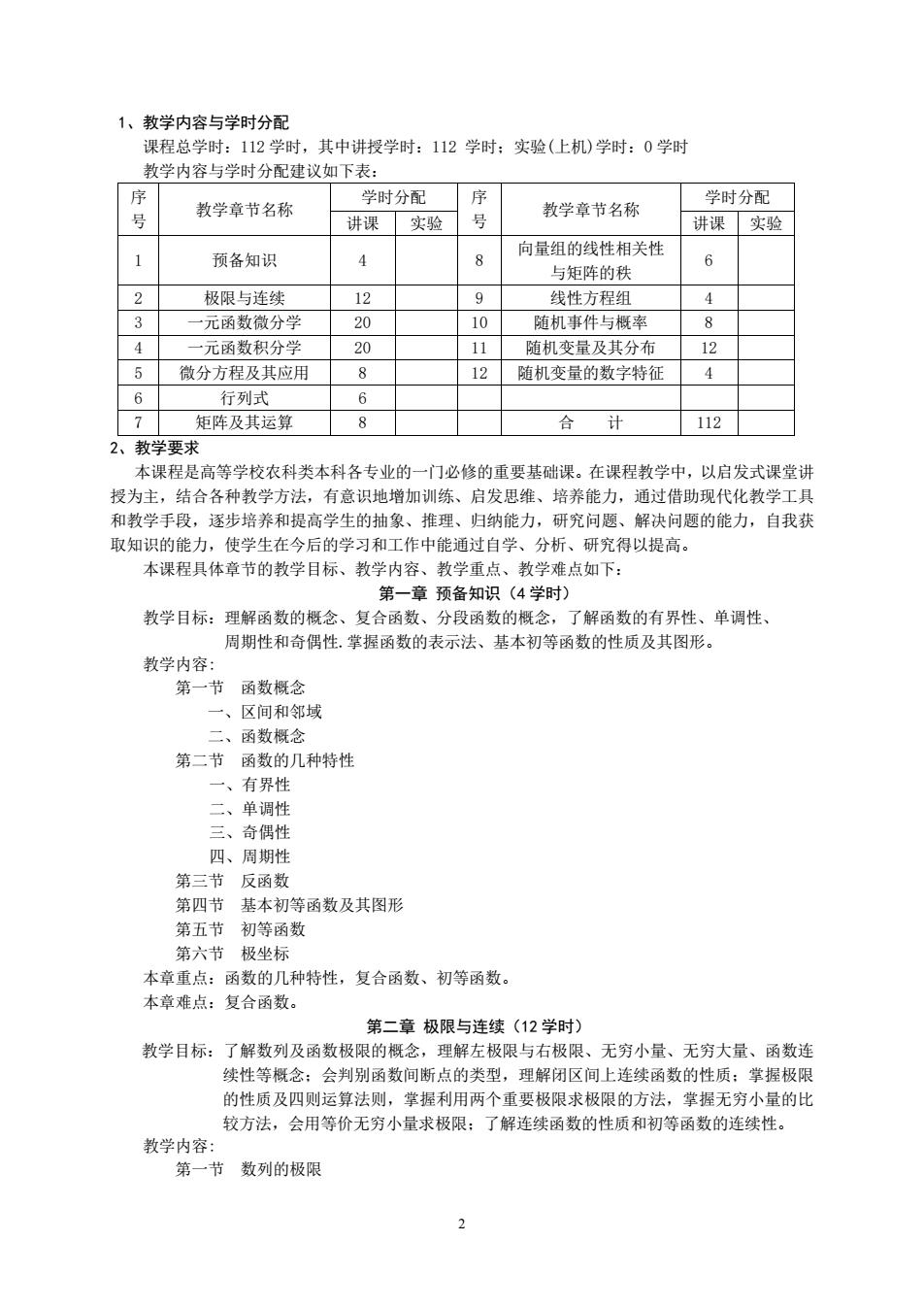
1、教学内容与学时分配 课程总学时:112学时,其中讲授学时:112学时:实验(上机)学时:0学时 教学内容与学时分配建议如下表: 教学章节名称 学时分配 序 学时分配 教学章节名称 号 进课实验号 讲课实验 向量组的线棒相关性 预备知识 4 8 与矩阵的形 2 极限与连续 12 9 线性方程组 4 3 一元函数微分学 20 10随机事件与概率 8 一元函数积分学 20 11 随机变量及其分布 12 5 微分方程及其应用 12随机变量的数字特征 6 们列式 6 7 矩阵及其运算 8 合 计 112 2、教学要 课程是高等学校农科类本科各专业的 门必修的重要基础课。在课程教学中,以启发式课堂 授为主,结合各种教学方法,有意识地增加训练、启发思维、培养能力,通过借助现代化教学工 和教学手段,逐步培养和提高学生的抽象、推理、归纳能力,研究问题、解决问题的能力,自我获 取知识的能力,使学生在今后的学习和工作中能通过自学、分析、研究得以提高。 本果程且体章节的教学目标、教学内容、教学重点、教学难点如下: 第一章预备知识(4学时) 教学目标:理解函数的概念、复合函数、分段函数的概念 了解函数的有界性、单调性、 周期性和奇偶性.掌握函数的表示法、基本初等函数的性质及其图形。 教学内容 第一节函数概念 ·、区间和邻域 函数概今 第二节 函数的几种特性 “、有界但 二、单调性 一、奇偶性 四、周期性 第二反函 第四节基本初等函数及其图形 第五节 初等函数 第六节极坐标 本章重点:函数的几种特性,复合函数、初等函数。 本音难占:复合函数。 第二章极限与连续(12学时) 教学目标:了解数列及函数极限的概念,理解左极限与右极限、无穷小量、无穷大量、函数道 续性等概念:会判别函数间断点的类型,理解闭区间上连续函数的性质:掌握极限 的性质及四则运算法则,掌握利用两个重要极限求极限的方法,掌据无穷小量的比 较方法,会用等价无穷小量求极限:了解连续函数的性质和初等函数的连续性。 教学内容: 第一节数列的极限
2 1、教学内容与学时分配 课程总学时:112 学时,其中讲授学时:112 学时;实验(上机)学时:0 学时 教学内容与学时分配建议如下表: 序 号 教学章节名称 学时分配 序 号 教学章节名称 学时分配 讲课 实验 讲课 实验 1 预备知识 4 8 向量组的线性相关性 与矩阵的秩 6 2 极限与连续 12 9 线性方程组 4 3 一元函数微分学 20 10 随机事件与概率 8 4 一元函数积分学 20 11 随机变量及其分布 12 5 微分方程及其应用 8 12 随机变量的数字特征 4 6 行列式 6 7 矩阵及其运算 8 合 计 112 2、教学要求 本课程是高等学校农科类本科各专业的一门必修的重要基础课。在课程教学中,以启发式课堂讲 授为主,结合各种教学方法,有意识地增加训练、启发思维、培养能力,通过借助现代化教学工具 和教学手段,逐步培养和提高学生的抽象、推理、归纳能力,研究问题、解决问题的能力,自我获 取知识的能力,使学生在今后的学习和工作中能通过自学、分析、研究得以提高。 本课程具体章节的教学目标、教学内容、教学重点、教学难点如下: 第一章 预备知识(4 学时) 教学目标:理解函数的概念、复合函数、分段函数的概念,了解函数的有界性、单调性、 周期性和奇偶性.掌握函数的表示法、基本初等函数的性质及其图形。 教学内容: 第一节 函数概念 一、区间和邻域 二、函数概念 第二节 函数的几种特性 一、有界性 二、单调性 三、奇偶性 四、周期性 第三节 反函数 第四节 基本初等函数及其图形 第五节 初等函数 第六节 极坐标 本章重点:函数的几种特性,复合函数、初等函数。 本章难点:复合函数。 第二章 极限与连续(12 学时) 教学目标:了解数列及函数极限的概念,理解左极限与右极限、无穷小量、无穷大量、函数连 续性等概念;会判别函数间断点的类型,理解闭区间上连续函数的性质;掌握极限 的性质及四则运算法则,掌握利用两个重要极限求极限的方法,掌握无穷小量的比 较方法,会用等价无穷小量求极限;了解连续函数的性质和初等函数的连续性。 教学内容: 第一节 数列的极限

一、数列极限的定义 二、收敛数列的性质 第二节函数的极限 ,x一→时函数的极限 二、x→X0时函数的极限 第三节极限的运算法则及存在准则 一、极限的四则运算 个重要极限 第四节无 小量与无穷大量 一、无穷小量 二、无穷大量 三、无穷小量与无穷大量的关系 第五节函数的连续性 连续概今 二、间断点的分类 三、闭区间上连续函数的性质 本章重点:极限的概今及坛算性质,两个重要极限,函数连续的督今 本章难点:极限的概念,两个重要极限,闭区间上连续函数的性质及其应用。 第三章 一元函数微分学(20学时) 教学目标:理解导数 分的概念 导数的几何意义 函数的可导性与连续性之间的关系 解高阶导数的概念,:掌握导数的四则运算法则和复合函数的求导法则,掌握基本初 等函数的导数公式,会求分段函数的导数、隐函数和由参数方程所确定的函数的导 数:会求简单函数的高阶导数及平面曲线的切线方程和法线方程:了解微分的四则 运算法则和一阶微分形式的不变性,会求函数的微分:理解并会用罗尔定理、拉格 朗日中值定理,掌握用洛必达法则 解函数的极值概念 判断函数 单调性和求函数极值的方法,函数的最大值和最小值的求法及其应用.会用导数判断 函数图形的凹凸性以及求函数图形的拐点以及水平、铅直渐近线。 教学内容: 第一节导数概今 导数定义及几何意义 可导性与连续性关系 第二节求导法则 一、函数和、差、积、商的求导法则 二、反函数的导数 、复合函数求导公式 四、基本求导法则与公式 第三节高阶导数 一、高阶导数定义 二、高阶导数的计算方法 第四节隐函数与参数方程确定的函数的导数 隐函数求导法贝 、参数方程确定的函数的导数 第五节微分
3 一、数列极限的定义 二、收敛数列的性质 第二节 函数的极限 一、 x → 时函数的极限 二、 0 x → x 时函数的极限 第三节 极限的运算法则及存在准则 一、极限的四则运算 二、两个重要极限 第四节 无穷小量与无穷大量 一、无穷小量 二、无穷大量 三、无穷小量与无穷大量的关系 第五节 函数的连续性 一、连续概念 二、间断点的分类 三、闭区间上连续函数的性质 本章重点:极限的概念及运算性质,两个重要极限,函数连续的概念。 本章难点:极限的概念,两个重要极限,闭区间上连续函数的性质及其应用。 第三章 一元函数微分学(20 学时) 教学目标:理解导数和微分的概念、导数的几何意义、函数的可导性与连续性之间的关系,了 解高阶导数的概念,;掌握导数的四则运算法则和复合函数的求导法则,掌握基本初 等函数的导数公式. 会求分段函数的导数、隐函数和由参数方程所确定的函数的导 数;会求简单函数的高阶导数及平面曲线的切线方程和法线方程;了解微分的四则 运算法则和一阶微分形式的不变性,会求函数的微分;理解并会用罗尔定理、拉格 朗日中值定理,掌握用洛必达法则;理解函数的极值概念,掌握用导数判断函数的 单调性和求函数极值的方法,函数的最大值和最小值的求法及其应用.会用导数判断 函数图形的凹凸性以及求函数图形的拐点以及水平、铅直渐近线。 教学内容: 第一节 导数概念 一、导数定义及几何意义 二、可导性与连续性关系 第二节 求导法则 一、函数和、差、积、商的求导法则 二、反函数的导数 三、复合函数求导公式 四、基本求导法则与公式 第三节 高阶导数 一、高阶导数定义 二、高阶导数的计算方法 第四节 隐函数与参数方程确定的函数的导数 一、隐函数求导法则 二、参数方程确定的函数的导数 第五节 微分

一、微分定义 二、微分基本公式与运算法则 第六节微分中值定理 罗尔定理 二、拉格明日中值定理 三、柯西中值定理 第七节罗必达法则 第八节函数的单调性判别法 单调性判别法 、利用单调性证明不等式 第九节函数的极值与最大(小)值 一、函数的极值和求法 二、函数的最大(小)值 第十节曲线的凸性、 拐点与渐近线 第十 节函数的作图 本章重点:导数概念,求导法则,微分的概念及运算法则,中值定理及其应用,洛必达法则, 函数的单调性与曲线的凹凸性,函数的极值与最值。 本章难点:导数与微分概念,复合函数、隐函数求导法则,中值定理及其应用。 第四音一元承数积分学(20学时) 教学目标:理解原函数、不定积分和定积分的概念,掌握不定积分的基本公式、不定积分和定 积分的性质及定积分中值定理:掌握换元积分法与分部积分法,会求有理函数、 角函数有理式和简单无理函数的积分:理解积分上限的函数,会求它的导数:掌握 牛顿莱布尼茨公式:了解反常积分的概念,会计算反常积分:掌握用定积分表达和 十算一些几何量 数学内容 第一原承粉与不定积分的参 不定积分的概念 不定积分的基本公式 第一节换元积分法 ·、第一类换元法 一 ,第二类换元法 第三节 分部积分 第四节 简单有理函数的积分法 一、有理真分式的分解 二、部分分式的积分 第五节定积分概念与性质 足 性 第六节 微积分基本定理 第七节定积分的计算 一、定积分的换元积分法 定积分的分步积分法 第八节 积分的应用 、定积分的微元法 二、定积分在几何上的应用
4 一、微分定义 二、微分基本公式与运算法则 第六节 微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 第七节 罗必达法则 第八节 函数的单调性判别法 一、单调性判别法 二、利用单调性证明不等式 第九节 函数的极值与最大(小)值 一、函数的极值和求法 二、函数的最大(小)值 第十节 曲线的凸性、拐点与渐近线 第十一节 函数的作图 本章重点:导数概念,求导法则,微分的概念及运算法则,中值定理及其应用,洛必达法则, 函数的单调性与曲线的凹凸性,函数的极值与最值。 本章难点:导数与微分概念,复合函数、隐函数求导法则,中值定理及其应用。 第四章 一元函数积分学(20 学时) 教学目标:理解原函数、不定积分和定积分的概念,掌握不定积分的基本公式、不定积分和定 积分的性质及定积分中值定理;掌握换元积分法与分部积分法,会求有理函数、三 角函数有理式和简单无理函数的积分;理解积分上限的函数,会求它的导数;掌握 牛顿-莱布尼茨公式;了解反常积分的概念,会计算反常积分;掌握用定积分表达和 计算一些几何量。 教学内容: 第一节 原函数与不定积分的概念 一、不定积分的概念与性质 二、不定积分的基本公式 第二节 换元积分法 一、第一类换元法 二、第二类换元法 第三节 分部积分法 第四节 简单有理函数的积分法 一、有理真分式的分解 二、部分分式的积分 第五节 定积分概念与性质 一、曲边梯形的面积 二、定积分的定义和性质 第六节 微积分基本定理 第七节 定积分的计算 一、定积分的换元积分法 二、定积分的分步积分法 第八节 定积分的应用 一、定积分的微元法 二、定积分在几何上的应用

第九节反常积分 一、无穷限的反常积分 二、无界函数的反常积分 本章重点:不定积分的概念 性质与积分方法,定积分的概念与性质,微积分学基本公式,定 积分的微元法,定积分在几何中的应用。 本章难点:基本积分法,变上限定积分的性质及应用,定积分的微元法。 第五章微分方程初步(8学时) 教学目标:了解微分方程及其阶、解、通解、初始条件和特解等概念:掌握变量可分离 的高阶微分方程:理解 线性微分方程的解法:会用微分方程解决一些简单的应用问题, 教学内容: 第一节微分方程的基本概念 第二节 一阶微分方程 可分离变量的微分方程 二、齐次微分方程 一阶线性微分方程 第三节高阶微分方程 一、可降阶的高阶微分方程 二、线性微分方程解的结构 价常系数齐次线性微分方程 四、二阶常系数非齐次线性微分方程 第四节微分方程的应用 本章重点:可分离变量的微分方程,一阶线性微分方程,二阶常系数线性微分方程 本章难点: 一阶线性微分方程,二阶常系数非齐次线性微分方程。 第六章行列式 (6学时 教学目标:了解行列式的概念。 掌握行列式的性质及用行列式的性质和行列式按行(列) 展开定理计算行列式。 教学内容: 第一节行列式的定义 三阶行列式 二、列 三、n阶行列式的定义 第一节行列式的性质 第三节行列式的展开定理 、余子式和代数余子式 、行列式按 (列)展开定理 第四节n阶行列式的计算 一、三角行列式 二、对称行列式、反对称行列式 三、行列式按行(列)展开 四、范德蒙行 列式 第五节克莱姆法 一、克莱姆法则
5 第九节 反常积分 一、无穷限的反常积分 二、无界函数的反常积分 本章重点:不定积分的概念、性质与积分方法,定积分的概念与性质,微积分学基本公式,定 积分的微元法,定积分在几何中的应用。 本章难点:基本积分法,变上限定积分的性质及应用,定积分的微元法。 第五章 微分方程初步(8 学时) 教学目标:了解微分方程及其阶、解、通解、初始条件和特解等概念;掌握变量可分离 的微分方程及一阶线性微分方程的解法,会解齐次微分方程;会用降阶法解可降阶 的高阶微分方程;理解二阶线性微分方程解的性质及解的结构定理.掌握二阶常系数 线性微分方程的解法;会用微分方程解决一些简单的应用问题. 教学内容: 第一节 微分方程的基本概念 第二节 一阶微分方程 一、可分离变量的微分方程 二、齐次微分方程 三、一阶线性微分方程 第三节 高阶微分方程 一、可降阶的高阶微分方程 二、线性微分方程解的结构 三、二阶常系数齐次线性微分方程 四、二阶常系数非齐次线性微分方程 第四节 微分方程的应用 本章重点:可分离变量的微分方程,一阶线性微分方程,二阶常系数线性微分方程。 本章难点:一阶线性微分方程,二阶常系数非齐次线性微分方程。 第六章 行列式(6 学时) 教学目标:了解行列式的概念,掌握行列式的性质及用行列式的性质和行列式按行(列) 展开定理计算行列式。 教学内容: 第一节 行列式的定义 一、二、三阶行列式 二、排列 三、n 阶行列式的定义 第二节 行列式的性质 第三节 行列式的展开定理 一、余子式和代数余子式 二、行列式按行(列)展开定理 第四节 n 阶行列式的计算 一、三角行列式 二、对称行列式、反对称行列式 三、行列式按行(列)展开 四、范德蒙行列式 第五节 克莱姆法则 一、克莱姆法则