山东理工大学：《内燃机设计》课程教学资源（PPT讲稿）第三章 内燃机零件的强度计算基础

应力平斯微分方程 静力平衡条件：∑F=0,∑F,=0,∑F=0 直角坐标下的应力平衡微分方程米 00 1=0 (i,j=x,y,2) 00 dx 003+ ty 0ts=0 8x ay Totgdx ax Oxt asdx ar 8x ay x: Jr-dx 0=0 图3-4垂胄芋×轴截面上的应力分层

应力平衡微分方程 直角坐标下的应力平衡微分方程* 0 ij i    =  ( , , , ) i j x y z = 0 0 0 x xz xy yx y yz zx zy z x y z x y z x y z             + + =          + + =         + + =     0, 0, 0 静力平衡条件：    F F F x y z = = =

圆柱坐标下的应力平微分方程 00,1 t Or rp +0rz+(o,-o,)=0 1 2 。=0 Or r ap Oz 1t9+ Or ∂0 8z

圆柱坐标下的应力平衡微分方程 0 1 0 1 2 ( ) 0 1 1 + =   +   +   + =   +   +   + − =   +   +   r r z r r r z r r r z r z r z z r z r z r r r z r r r                      

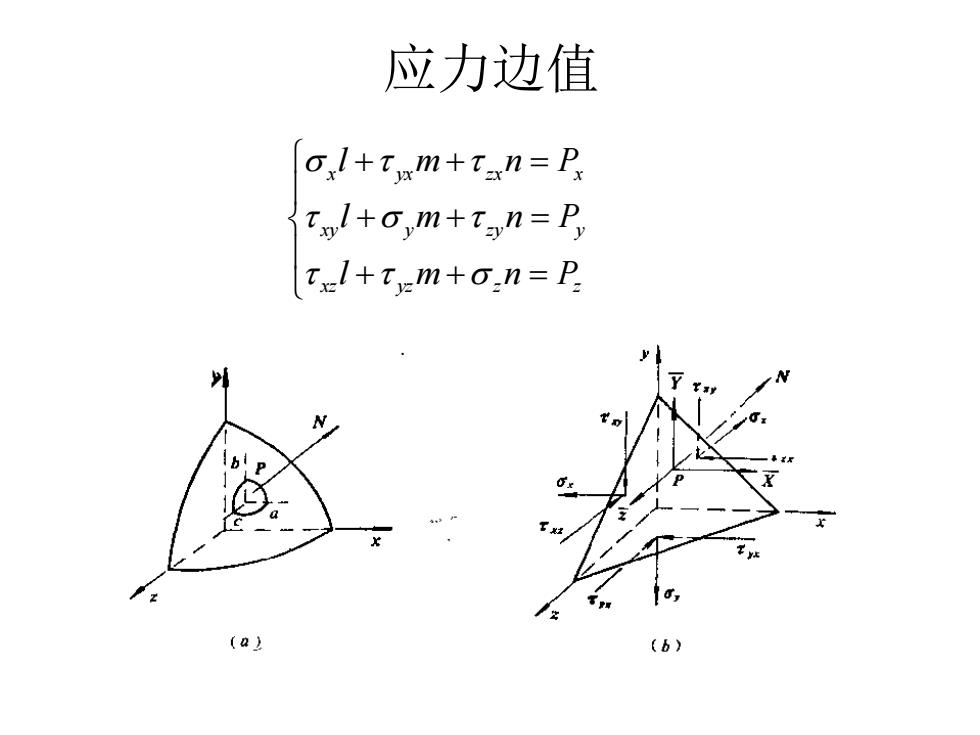
应力边值 l+tmm+tan=P Tol+o,m+tan=P Txl+tm+o.n=P N (a

应力边值 x yx zx x xy y zy y xz yz z z l m n P l m n P l m n P           + + =   + + =  + + = 

五、协调方程 六个应变分量间的微分关系式 变形的协调性 “撕裂”“套叠” 2 ar2 Oxay 26, y 0c2 02 aydz 变形前 变形后“断裂” 变形后“套叠” 变形协调 0y 0r2 022 0z0x 2 a aYg OY OY ayoz 8x 82 2 OY OY 8zOx ay 8x ay Oz 0 2 ∂ys- Y) Oxoy 0z Ox 8y 82

五、协调方程 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ( ) 2 ( ) 2 ( ) x y xy y yz z z x zx x zx yz xy y yz xy zx z yz xy zx y x x y z y y z x z z x y z x x y z z x y x y z x y z x y z                         + =        + =        + =          = − + +            = − +            = + −       变形的协调性 “撕裂” “套叠” 六个应变分量间的微分关系式

六、弹性力学问题的求解 三维： 15个未知量，即3个位移分量，6个应变 分量，6个应力分量； 15个方程，即3个平衡方程，6个几何方 程，6个物理方程。 求解弹性力学有限元法有2种： 直接法，它的优点是直观易于理解但对于温 度场、流场等非结构问题不便于使用； 变分法，其中位移法用的是最小位能原理或 虚位移原理，而应力法用的是最小位能原 理，这些原理都是以小变形为前提的

六、弹性力学问题的求解 三维： １５个未知量，即３个位移分量，６个应变 分量，６个应力分量； １５个方程，即３个平衡方程，６个几何方 程，６个物理方程。 求解弹性力学有限元法有２种： 直接法，它的优点是直观易于理解但对于温 度场、流场等非结构问题不便于使用； 变分法，其中位移法用的是最小位能原理或 虚位移原理，而应力法用的是最小位能原 理，这些原理都是以小变形为前提的