山东理工大学：《内燃机设计》课程教学资源（PPT讲稿）第三章 内燃机零件的强度计算基础

+器d 应变符号规定： 8 正应变或线应变 B 伸长为正，缩短为负； 剪应变或切应变(8,8,6) 夹角减小为正，增大为负： dx 图3-3微元休剪应变示意图 Yn=ga+gB≈a+B=u+ dy dx

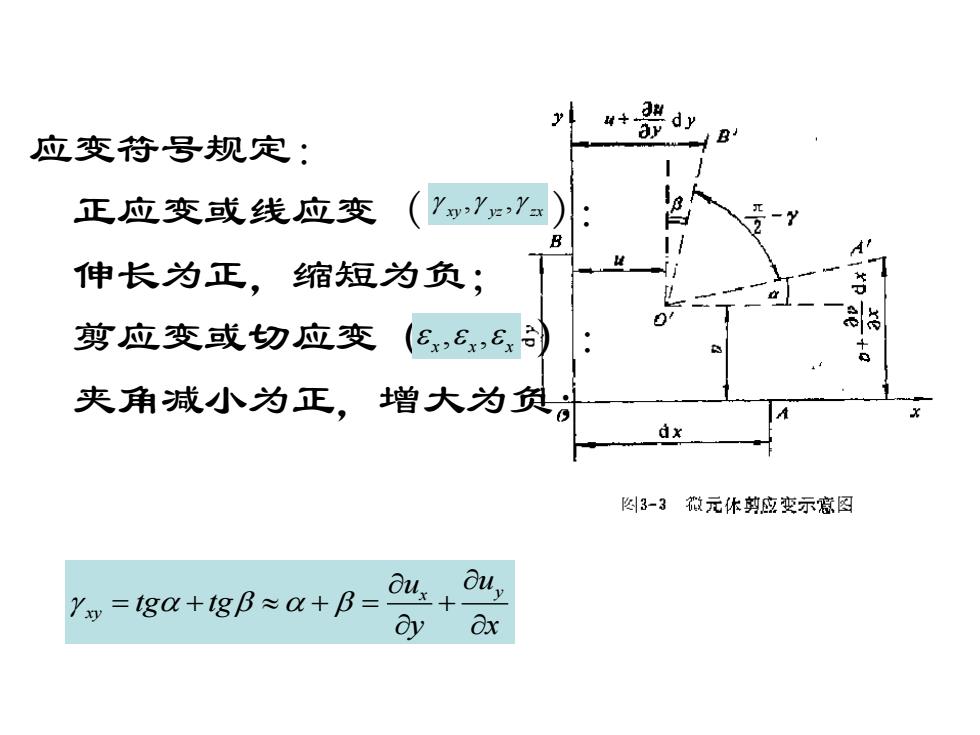
应变符号规定： 正应变或线应变 ( )： 伸长为正，缩短为负； 剪应变或切应变（ ）： 夹角减小为正，增大为负； x y xy u u tg tg y x        = +  + = +   , , xxx  , , xy yz zx 

1 Ex 2 {= {e} 。二 L

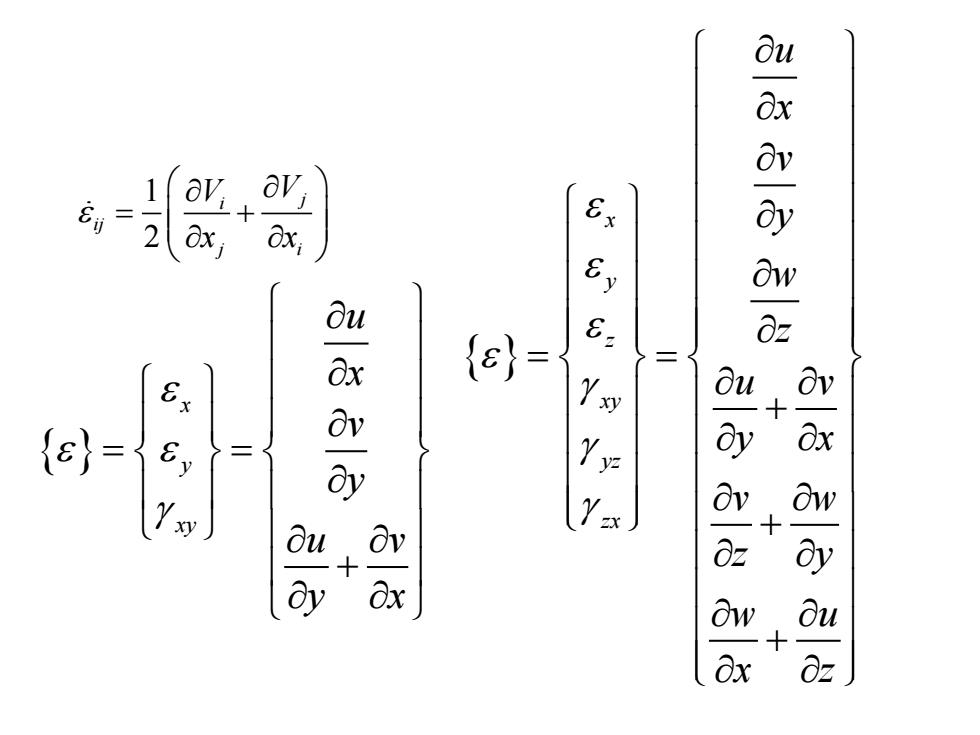
1 2 j i ij j i V V x x      = +           x y z xy yz zx u x v y w z u v y x v w z y w u x z                                          = =           +           +           +         x y xy u x v y u v y x                    = =                  +    

三、应力-应变方程 应力表示本构方程 E=2a,-o,+o,】=+0-o1 ,-4o,+a】=E【I+0o,-O] 1 E E E. lo. (a,+o,】=E[1+Wa:-O] G •E为弹性模量 •G为剪切弹性模量 Y G ·“为横向变形系数—泊松比 Yx G E G- 2(1+)

三、应力-应变方程 应力表示本构方程 1 1 [ ( )] [(1 ) ] 1 1 [ ( )] [(1 ) ] 1 1 [ ( )] [(1 ) ] x x y z x y y x z y z z x y z xy xy yz yz xz xz E E E E E E G G G                               = − + = + −  = − + = + −  = − + = + −  = = = •E为弹性模量 •G为剪切弹性模量 •  为横向变形系数——泊松比 2(1 ) E G  = +

泊松 法国数学家、物理学家和力学家

泊松 法国数学家、物理学家和力学家

应变-应力 {o}=[D]{&} 对 1-4 41 1-4 1-4 (DI= E(1-4） 1+41-2)） 0 00 1-24 称 21-4）) 0 00 1-2u 0 21-4） 0 00 1-24 21-4)

应变-应力 1 1 1 1 1 1 (1 ) [ ] 1 2 (1 )(1 2 ) 0 0 0 2(1 ) 1 2 0 0 0 0 2(1 ) 1 2 0 0 0 0 0 2(1 ) E D                    − − − − =   − + −   − − − −   − 对 称 { } [ ]{ }   = D