七、变分法与最小位能原理 1.变分法概念 有限元法在数学上是属于变分法的范畴。 泛函是函数的函数,而对泛函求极值称为变分。 变分问题的简例: y[ (x) T-fd =6 1+y2d
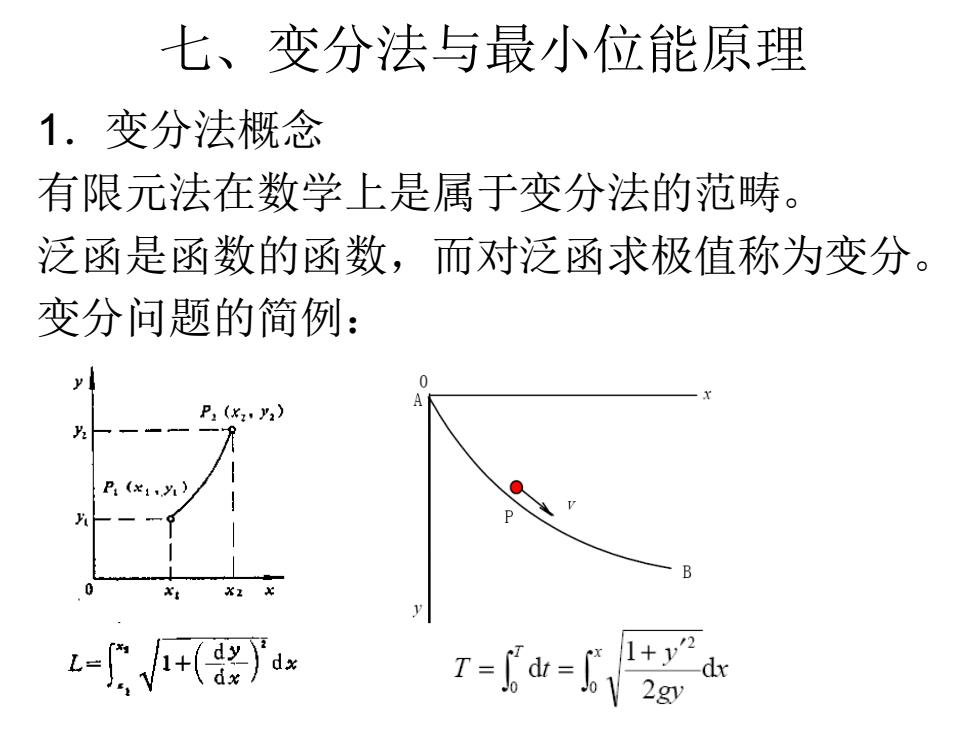
七、变分法与最小位能原理 1.变分法概念 有限元法在数学上是属于变分法的范畴。 泛函是函数的函数,而对泛函求极值称为变分。 变分问题的简例:

考虑著名的最速降线落径问题。如图17.1所示 已知A和B为不在同一铅垂线和不同高度的两点,要求 找出A、B间的这样一条曲线,当一质点在重力作用下沿 这条曲线无摩擦地从A滑到时,所需的时间T最小。 B(x,y) 图17.1
考虑著名的最速降线落径问题。如图17.1 所示, 已知A和B为不在同一铅垂线和不同高度的两点,要求 找出A、B间的这样一条曲线,当一质点在重力作用下沿 这条曲线无摩擦地从A滑到B时,所需的时间T最小. 图17.1

我们知道,此时质点的速度是 ds dt 因此从A滑到B所需的时间为 -e房” 即为 几w- 2gy c(17.1i0
我们知道,此时质点的速度是 因此从 A滑到B所需的时间为 即为 (17.1.1)

式中少代表对X求一阶导数.我们称上述的T为 y(x)的泛函,而称y(x)为可取的函数类,为泛函TLy(x)] 的定义域。简单地说,泛函就是函数的函数(不是复合函数 的那种含义)。 一般来说,设C是函数的集合,B是实数或复数的集合 如果对于C的任一元素y(X)在B中都有一个元素J与之对应
式中 代表对 求一阶导数.我们称上述的 为 的泛函,而称 为可取的函数类,为泛函 的定义域。简单地说,泛函就是函数的函数(不是复合函数 的那种含义). 一般来说,设C是函数的集合,B是实数或复数的集合, 如果对于C的任一元素 在B中都有一个元素 与之对应

则称J为y(x)的泛函,记为 J=Jy(x)] 必须注意,泛函不同于通常讲的函数.决定 通常函数值的因素是自变量的取值,而决定泛函的值 的因素则是函数的取形.如上面例子中的泛函的变化 是由函数y(x) 本身的变化(即从A到B的不同曲线) 所引起的。它的值既不取决于某一个X值,也不取决 于某一个 V值,而是取决于整个集合C中y与X 的函数关系
则称 为 的泛函,记为 必须注意,泛函不同于通常讲的函数.决定 通常函数值的因素是自变量的取值,而决定泛函的值 的因素则是函数的取形.如上面例子中的泛函T的变化 是由函数 本身的变化(即从A到B的不同曲线) 所引起的.它的值既不取决于某一个 值,也不取决 于某一个 值,而是取决于整个集合C中 与 的函数关系.