
Φ =Φ21+1。(3)耦合系数k(或称耦合因数i漏磁通%¥一般情况下,一个线圈通电后所十产生的磁通只有一部分与邻近线圈ui1交链,另一部分称为漏磁通。漏磁福通越少,互感线圈之间的耦合程度d21越紧密。工程上常用耦合系数k表L2U2“资料!示其紧密程度:Y12[21k=1 称全耦合:漏磁 Φl。=Φ2=0kY2Yi1即 Φi1= Φ21, Φ22=Φ12 oMMk=吕两线圈结构、相互几VL,LVOL:OL何位置和周围磁介质有关一般 0≤k≤16
SDUT 内 部 资 料! 请 勿 外 传! (3)耦合系数k(或称耦合因数) 6 k= Y12 Y11 · Y21 Y22 k = M 0 ≤k≤ 1 L1 L2 k 与两线圈结构、相互几 何位置和周围磁介质有关。 漏 磁 通 F1s F11 =F21+F1s L1 L2 i1 F21 u1 u2- + - + k=1 称全耦合: 漏磁 F1s =F2s =0 即 F11= F21 , F22 =F12。 一般 一般情况下,一个线圈通电后所 产生的磁通只有一部分与邻近线圈 交链,另一部分称为漏磁通。漏磁 通越少,互感线圈之间的耦合程度 越紧密。工程上常用耦合系数 k 表 示其紧密程度: L1 L2 M =

2.耦合电感的伏安关系D每一线圈都有自磁链与互磁链,同样每一线圈的电压都有自感2d22电压与互感电压i22'02内di01'一十- uz+ui土Mui=u11+u12=L-dtdizU2=U22+U21= L2±MdtU,= joL,i, ± joMi相量形式方程为:U,- jol,i, +joMiZM=joM,为互阻抗。其中のM互感抗
SDUT 内 部 资 料! 请 勿 外 传! - u1 + - u2 + 7 每一线圈都有自磁链 与互磁链,同样每一 线圈的电压都有自感 电压与互感电压。 u1=u11+u12= L1dt di1 M dt di2 u2=u22+u21= L2dt di2 M dt di1 2.耦合电感的伏安关系 . U1= jL1 .I1 jM .I2 . U2= jL2 .I2 jM .I1 ZM= jM,为互阻抗。其中M为互感抗。 相量形式方程为: 1' 1 F11 2' 2 F21 i2 F22 F12

3.耦合电感的同名端长对互感电压:因产生该电压的电流在另一线圈上,因此,要确定其符号,就必须知道两个线圈的绕向。unM102'M在电路图中也实际的互感线圈是封闭的,看不出绕向无法反映绕向请为解决这个问题,引入同名端的概念。多传!8
SDUT 内 部 资 料! 请 勿 外 传! 因产生该电压的电流在另一线圈上, 因此,要确定其符号,就必须知道两个线圈的绕向。 8 3. 耦合电感的同名端 对互感电压: L1 L2 + - + - u1 u2 i1 i2 1 1' 2 2' M 实际的互感线圈是封 闭的,看不出绕向 在电路图中也 无法反映绕向 为解决这个问题,引入同名端的概念
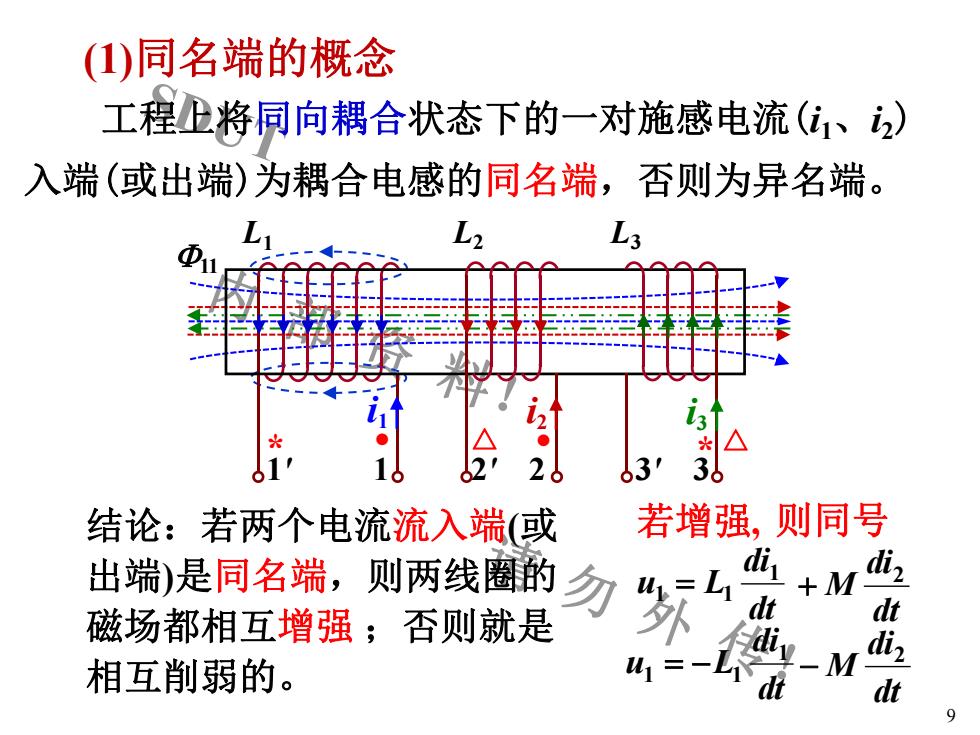
(1)同名端的概念工程卫将同向耦合状态下的一对施感电流(i、i)入端(或出端)为耦合电感的同名端,否则为异名端L2L3A*3!13'则同号若增强,结论:若两个电流流入端(或didi,出端)是同名端,则两线圈的勿人业山外磁场都相互增强;否则就是Fu相互削弱的。dtdt9
SDUT 内 部 资 料! 请 勿 外 传! (1)同名端的概念 1' 1 2' 2 3' 3 9 工程上将同向耦合状态下的一对施感电流(i1、i2) 入端(或出端)为耦合电感的同名端,否则为异名端。 F11 * • △ • * △ L1 L2 L3 i2 i3 i1 结论:若两个电流流入端(或 出端)是同名端,则两线圈的 磁场都相互增强 ;否则就是 相互削弱的。 dt di u L 1 1 = 1 dt di M 2 + 若增强, 则同号 dt di u L 1 1 = - 1 dt di M 2 -
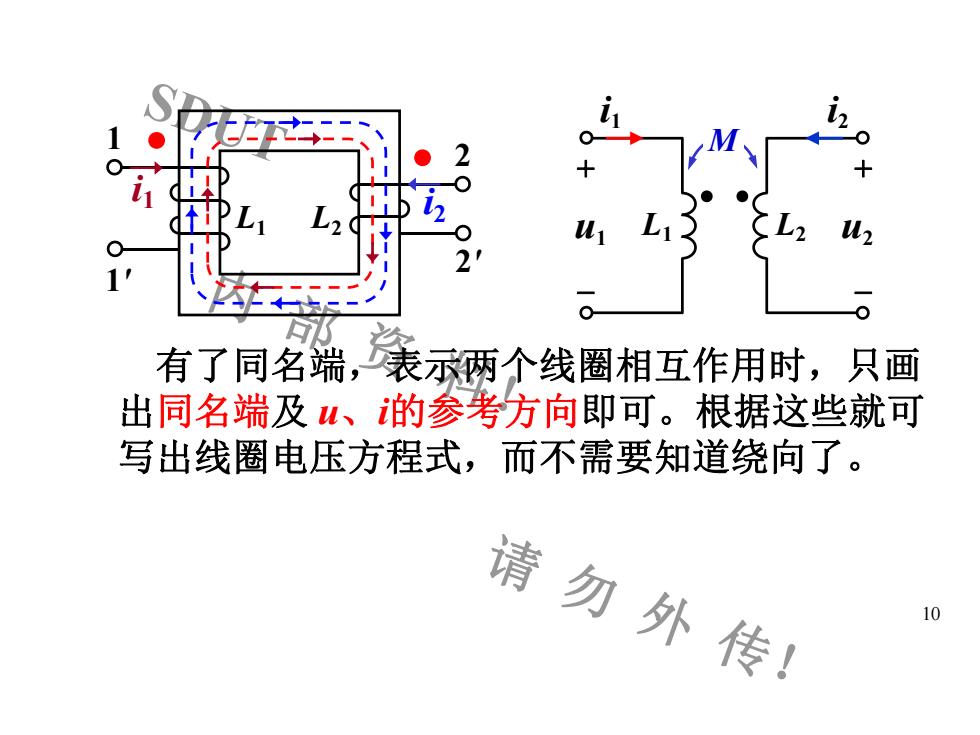
O2++O1MO12C2'1oo司有了同名端,表示两个线圈相互作用时,只画出同名端及u、的参考方向即可。根据这些就可写出线圈电压方程式,而不需要知道绕向了。请勿外传!10
SDUT 内 部 资 料! 请 勿 外 传! 10 M L1 + -u1 i1 L2 + -u2 i2 1 1' 2 2' L1 L2 i1 • i2 • 有了同名端,表示两个线圈相互作用时,只画 出同名端及 u、i的参考方向即可。根据这些就可 写出线圈电压方程式,而不需要知道绕向了