
Adaptive Learning Rates Popular Simple Idea:Reduce the learning rate by some factor every few epochs. At the beginning,we are far from the destination,so we use larger learning rate After several epochs,we are close to the destination,so we reduce the learning rate E.g.1/t decay:n=n/vt+1 Learning rate cannot be one-size-fits-all Giving different parameters different learning rates
Adaptive Learning Rates • Popular & Simple Idea: Reduce the learning rate by some factor every few epochs. • At the beginning, we are far from the destination, so we use larger learning rate • After several epochs, we are close to the destination, so we reduce the learning rate • E.g. 1/t decay: 𝜂 𝑡 = 𝜂Τ 𝑡 + 1 • Learning rate cannot be one-size-fits-all • Giving different parameters different learning rates

aL(0) Adagrad nt vt+1 gt 0w Divide the learning rate of each parameter by the root mean square of its previous derivatives Vanilla Gradient descent wt+1←wt-ng w is one parameters Adagrad ot:root mean square of w+1←wt_刀 the previous derivatives of parameter w Parameter dependent
Adagrad • Divide the learning rate of each parameter by the root mean square of its previous derivatives 𝜎 𝑡 : root mean square of the previous derivatives of parameter w w is one parameters 𝑔 𝑡 = 𝜕𝐿 𝜃 𝑡 𝜕𝑤 Vanilla Gradient descent Adagrad 𝑤𝑡+1 ← 𝑤𝑡 − 𝜂 𝑡𝑔 𝑡 𝜂 𝑡 = 𝜂 𝑡 + 1 𝑤𝑡+1 ← 𝑤𝑡 − 𝜂 𝑡 𝜎 𝑡 𝑔 𝑡 Parameter dependent
ot:root mean square of the previous derivatives of Adagrad parameter w w1←w0一 o090 0=V(g)2 w2←w1- 91 01=【g2+g鬥 w3←w22 0292 2-层g92+g+g1 w+1←wt-刀 1 t+ g)2 0
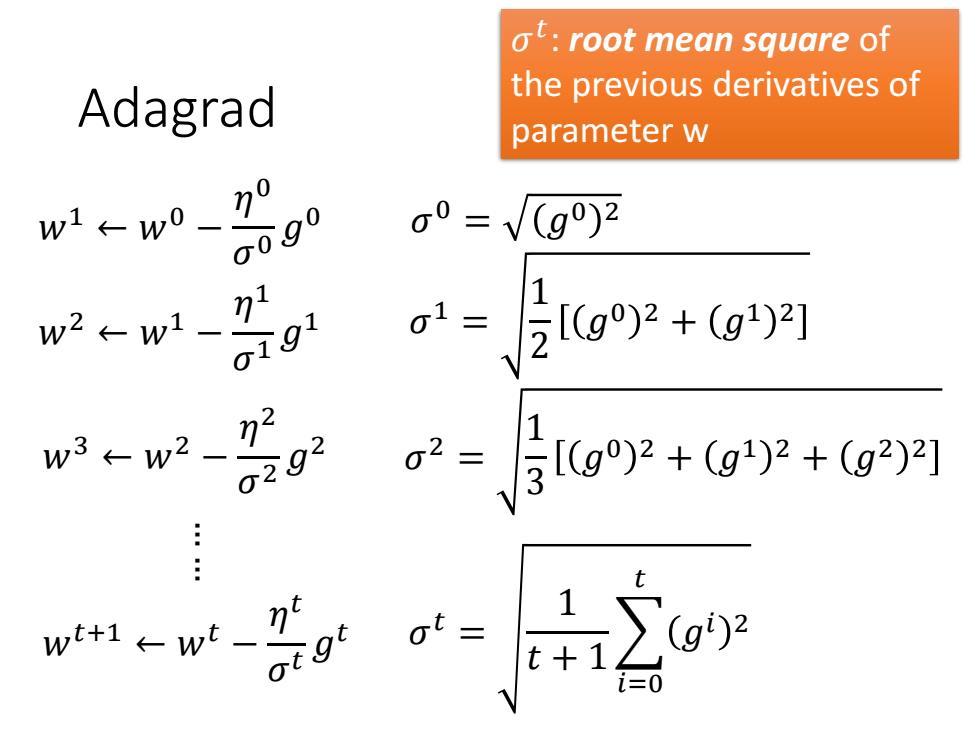
Adagrad 𝑤1 ← 𝑤0 − 𝜂 0 𝜎 0 𝑔 0 … … 𝑤2 ← 𝑤1 − 𝜂 1 𝜎 1 𝑔 1 𝑤𝑡+1 ← 𝑤𝑡 − 𝜂 𝑡 𝜎 𝑡 𝑔 𝑡 𝜎 0 = 𝑔0 2 𝜎 1 = 1 2 𝑔0 2 + 𝑔1 2 𝜎 𝑡 = 1 𝑡 + 1 𝑖=0 𝑡 𝑔𝑖 2 𝑤3 ← 𝑤2 − 𝜂 2 𝜎 2 𝑔 2 𝜎 2 = 1 3 𝑔0 2 + 𝑔1 2 + 𝑔2 2 𝜎 𝑡 : root mean square of the previous derivatives of parameter w
Adagrad Divide the learning rate of each parameter by the root mean square of its previous derivatives n-vt+i 1/t decay wt+1←wt wt+1←wt ∑=o(g)2
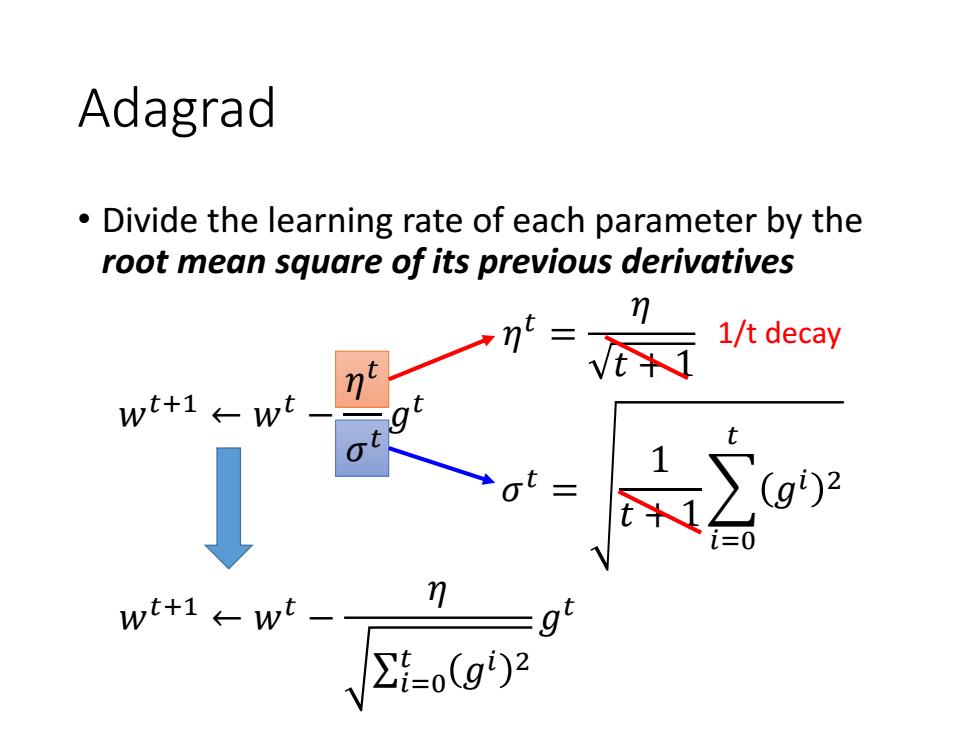
Adagrad • Divide the learning rate of each parameter by the root mean square of its previous derivatives 𝜂 𝑡 = 𝜂 𝑡 + 1 𝑤𝑡+1 ← 𝑤𝑡 − 𝜂 σ𝑖=0 𝑡 𝑔𝑖 2 𝑔 𝑡 1/t decay 𝑤𝑡+1 ← 𝑤𝑡 − 𝜂 𝜎 𝑡 𝑔 𝑡 𝜎 𝑡 = 1 𝑡 + 1 𝑖=0 𝑡 𝑔𝑖 2 𝜂 𝑡 𝜎 𝑡

Contradiction?-=vz gi= aL(0t) 0w Vanilla Gradient descent w+1←wt-ng Larger gradient, larger step Adagrad Larger gradient, w+1←wt、 larger step =9 (g2 Larger gradient, smaller step
Contradiction? 𝑤𝑡+1 ← 𝑤𝑡 − 𝜂 σ𝑖=0 𝑡 𝑔𝑖 2 𝑔 𝑡 Vanilla Gradient descent Adagrad Larger gradient, larger step Larger gradient, smaller step Larger gradient, larger step 𝑤𝑡+1 ← 𝑤𝑡 − 𝜂 𝑡𝑔 𝑡 𝑔 𝑡 = 𝜕𝐿 𝜃 𝑡 𝜕𝑤 𝜂 𝑡 = 𝜂 𝑡 + 1