第8章相量法 本章目录 8.1 复数 8.2 正弦量 8.3 相量法的基础 8.4 电路定律的相量形式

重点 口复数的表示和运算; ▣正弦量和相量之间的关系,正弦量的相位差和有 效值的概念; 口相量表示法; ▣ KCL、KVL的相量形式; 口R、L、C的相量形式; 霜与其它章节的联系 是学习第9、10、11、12章的基础。 必须熟练掌握相量法的解析运算
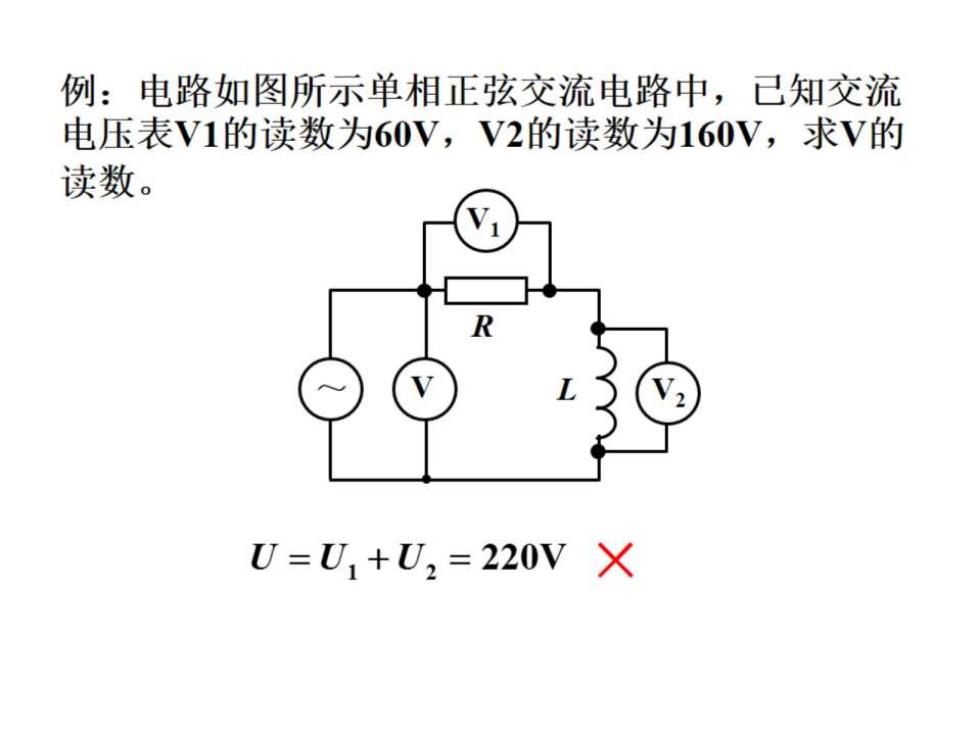
例:电路如图所示单相正弦交流电路中,已知交流 电压表V1的读数为60V,V2的读数为160V,求V的 读数。 U=U1+U,=220VX

§8-1复数 复数A可用复平面上的有向线段来表示。该有向 线段的长度A称为复数A的模,该有向线段与实轴 正方向的夹角0称为复数A的辐角。 A=Ae1o A=a+jb 复数F的实部a及虚部b与模及辐角0的关系为: a=Acoso =Va +b2 b=sino 0=aretan b
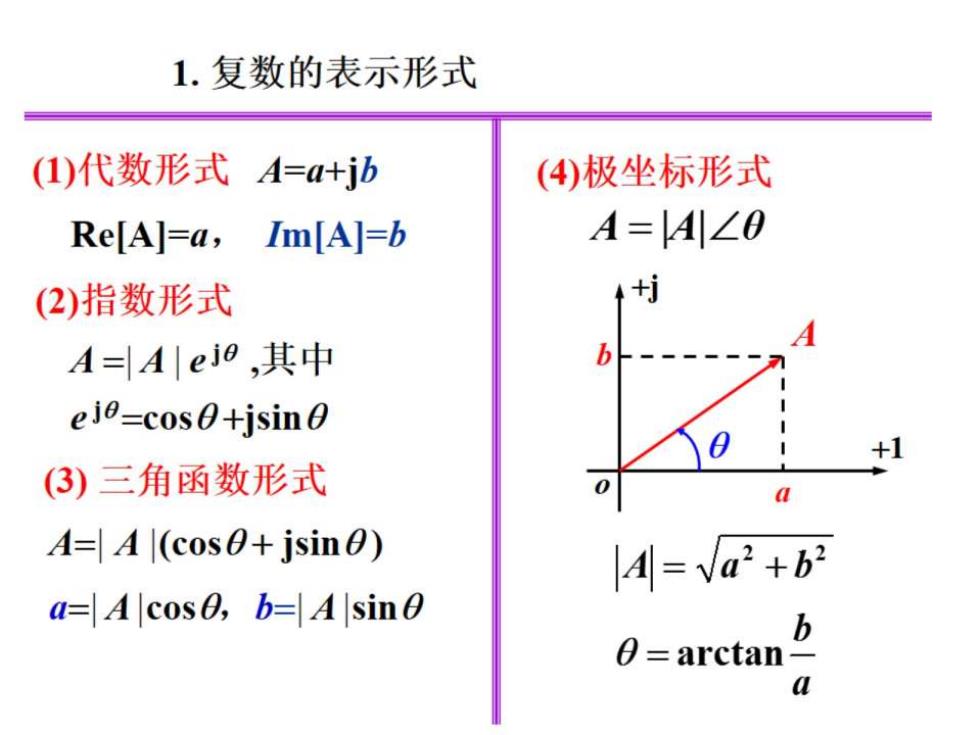
1.复数的表示形式 (1)代数形式A=a+ib (4)极坐标形式 Re[A]=a,Im[A]=b A=A∠0 (2)指数形式 A A=A|ej8,其中 b eio=cosO+jsin0 +1 (3)三角函数形式 0 A=A (cos0+jsin) A=va2+b2 a=A cos0,b=A sine 0=arctan-