
第四章 线性判别函数 2010-11-1
第四章 线性判别函数 2010-11-1

最小平方误差准则 (MSE)
最小平方误差准则 (MSE )
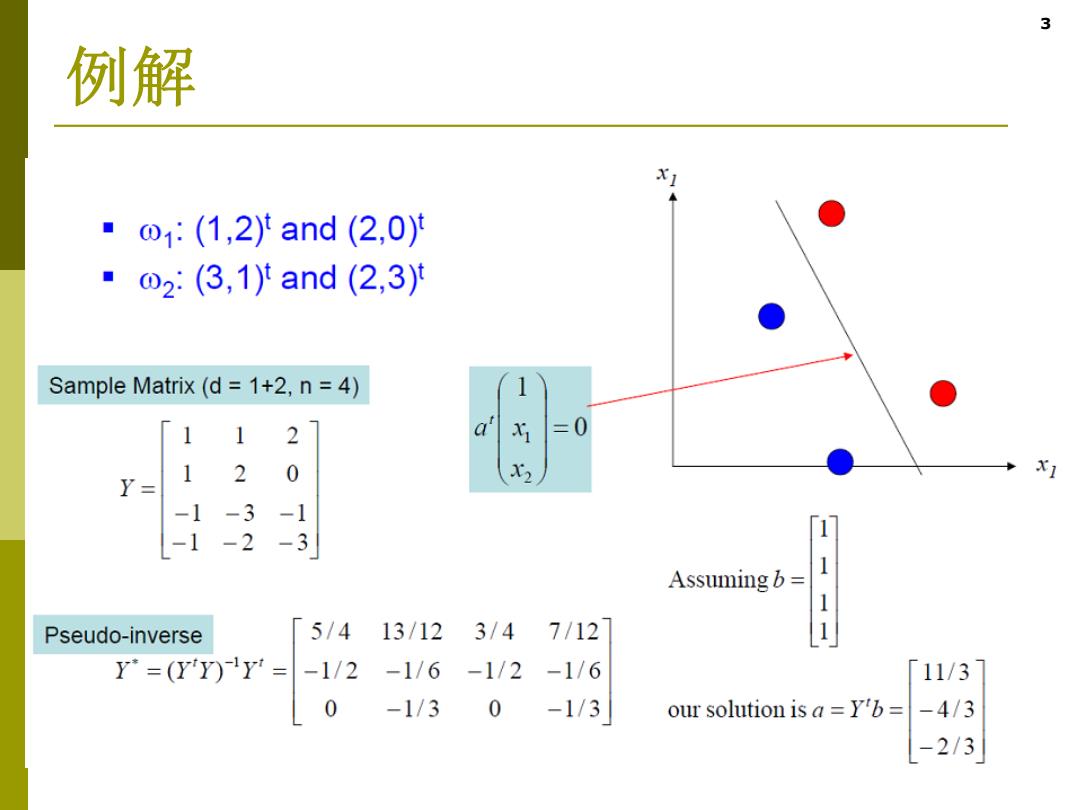
3 例解 ·o1(1,2)and(2,0) ■o2:(3,1)and(2,3) Sample Matrix(d 1+2,n=4) 1 2 1 =0 1 2 0 Y= -3 -1 -2 -3 「1 1 Assuming b Pseudo-inverse 5/4 13/12 3/4 7/12 i Y=(Y)r = -1/2 -1/6 -1/2 -1/6 11/3 0 -1/3 0 -1/3 our solution is a =Y'b= -4/3 -2/3
3 例解

MSE解与Bayes判别函数的关系 当N→∞,b=1n时,MSE的解以最小均方误差 逼近Bayes判别函数:g(x)=p(o|x)-p(o,|x): ■均方误差 e=fa'y-go(x)p(x)dx; 即有a=Y+b=argmine2. J,(a)=∑(a'y,-1)2+∑(ay,+1) X,∈01 X,∈02 =N 〔袋是er+梦m+ X,∈0 X∈02
4 MSE解与 Bayes 判别函数的关系 当 N→∞,b = 1n 时,MSE的解以最小均方误差 逼近 Bayes 判别函数: 均方误差 即有 01 2 gp p () ( xxx | ) ( | ); ;)()( 2 0 2 e dpg xxxyaT * 2 Y e argmin . a b 1 2 1 2 2 2 1 2 2 2 1 2 ( ) ( 1) ( 1) 1 1 ( 1) ( 1) ; i i i i T T si i T T i i J N N N NN NN x x x x a ay ay ay ay

MSE解与Bayes判别函数的关系 J,(a) N =P(@)J(a"y-1)p(xk)dx+P(@.)J(a"y+1)p(xrz)dx =∫(a'y-12pxo)dk+∫(ay-12px,o,)dk -Jtj+l-yoa》-+a p(x) -[(a'y)'p(x)dx-2J(a"y)go(x)p(xx+1 -J[a'y-g(xJp(xdk+[1-Jgi(x)p(xx =e2+[1-g6(x)p(x)本]
5 MSE解与 Bayes 判别函数的关系 2 1 2 1 2 1 2 2 2 1 1 2 2 2 2 1 2 2 0 0 (, ) (, ) (, ) (, ) 2 () (, ) (, ) ( ) ( ) ( 1) ( | ) ( ) ( 1) ( | ) ( 1) ( , ) ( 1) ( , ) () 2 ()() 1 ( ( ) T T T T T T T T T s p p p p pp p d p P p dP p d pd pd pd g pd g J N x x ay x x ay x x x x x ay x x ay x x ay x x ay x x ay x x ay x x x a y a 2 0 2 0 2 2 ) () 1 ()() 1 ()() ; pd g p e gp d d x xx x xx x xx