
第七章 特征的选择与提取 2010-11-29
第七章 特征的选择与提取 2010-11-29

基于概率分布的可分性判据
基于概率分布的可分性判据
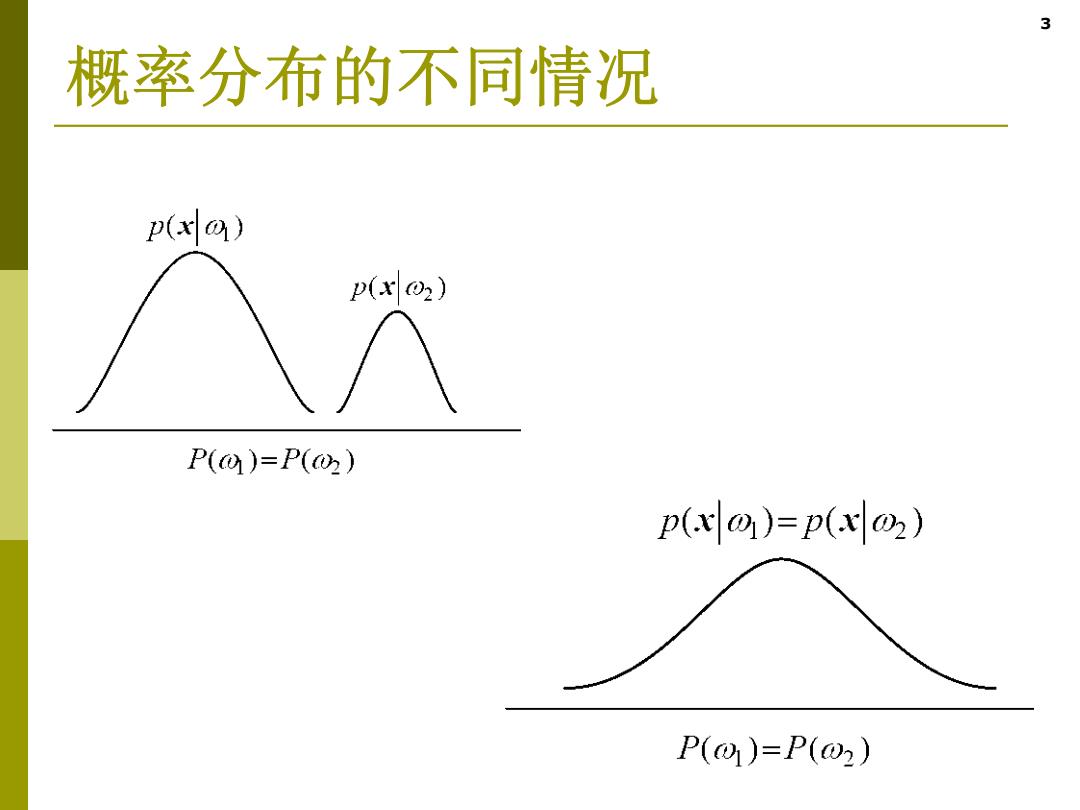
3 概率分布的不同情况 p(xa) p(x⊙2) P(0)=P() p(xo)=p(xo2) P()=P()
3 概率分布的不同情况

4 概率密度的距离 J()=Jg[p(xl@).p(xl@2).R.PJx 须满足的条件 1.,是非负,即J,≥0: 2. 当两类完全不交叠时,J,达到其最大值,即 if p(x)p(xl@2)=0,Vx,then J=J 3. 当两类分布密度相同时,J。=0: if p(xl@)=p(x|@2),Vx,then J=0
4 概率密度的距离 J ( ) ( | ), ( | ), , g p p PPd 1 2 12 xx x 须满足的条件 1. Jp 是非负,即 Jp ≥ 0; 2. 当两类完全不交叠时, Jp 达到其最大值,即 3. 当两类分布密度相同时, Jp = 0; 1 2 m a x if ( | ) ( | ) 0, , then ; p p p xx x J J 1 2 if ( | ) ( | ), , then 0. p pp J x xx

5 Bhattacharyya距离 J:=-In[Ip(xl@)p(xl@2)]dx 1)两类完全重合时,J3=0; 2)两类完全不交叠时,J=∞; 3)与错误概率的上界有直接关系: 卫≤[P(@,)P(o2exp(-Ja)】
5 Bhattacharyya 距离 1) 两类完全重合时, JB = 0; 2) 两类完全不交叠时, JB =∞; 3) 与错误概率的上界有直接关系: 1/2 1 2 ln [ ( | ) ( | )] B J pp d xx x 1 2 1 2 ( ) ( ) exp( ). PP P J e B