
第四章 线性判别函数 2010-10-27
第四章 线性判别函数 2010-10-27

2 例解 设两类样本的类内离散矩阵分别 S, 为S1,S2,各类样本均值分别为 1 m=(2,0),m2=(2,2),试用Fisher准 一方 则求其决策面方程。 20 S。=S+$2= 02 e-a 图中绿线为最佳分界面 y三W*X=y0; m+形2w*(m,+m) %= 三一→ 2 2 即(0,-1) 水3=-1 X2
2 例解 1 2 2 0 ; 0 2 wS SS 1 1 2 0.5 0 0 0 () ; 0 0.5 2 1 wS w mm 12 1 2 0 ( ) 1; 2 2 T m m y w mm 0 2 1 2 ; (0, 1) 1. T x y y x x w x 即

感知准则函数 (Perceptron)
感知准则函数 (Perceptron )

5 基本概念 口线性可分性:在特征空间中可以用一个线性分 界面正确无误地分开两类样本。 口在线性可分时,对合适的增广权向量a应有: 如果y∈o,则a'y>0; 如果y∈o2,则ay<0, 口样本的规范化:将第二类样本取其反向向量 y y 如果y∈o l-y 如果y∈o2 a'y>0 i=1,..N
5 基本概念 线性可分性:在特征空间中可以用一个线性分 界面正确无误地分开两类样本。 在线性可分时,对合适的增广权向量 a 应有: 样本的规范化:将第二类样本取其反向向量 1 2 , 0; , 0; T T y ay y ay 如果 则 如果 则 1 2 y y y y y 如果 = 如果 0 1,..., . T i a y i N
7 基本概念 解向量:满足ay:'>0,i=1,…,N的权向量 a; 口解区:权值空间中所有解向量组成的区域: solution solution region y2 region y2 a separating plane "separating plane
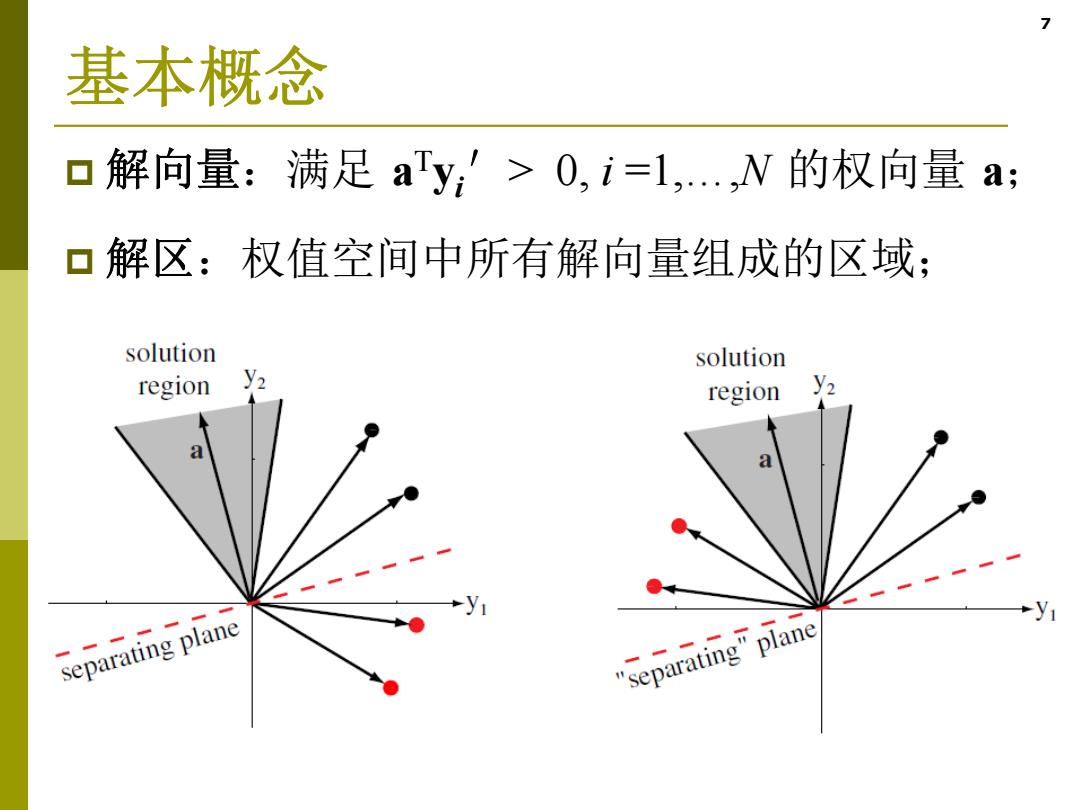
7 基本概念 解向量:满足 aTyi ′> 0, i =1,…,N 的权向量 a; 解区:权值空间中所有解向量组成的区域;