
罗点:0极点:子 所以X(z)的收敛域为: ◆jIm[z] D H< 为左边序列 12 0.5 Re[z] /2 2024/10/21 6
1 1 1 1 1 1 2 ( ) 1 1 3 1 1 1 2 2 4 z X z jz jz z − − − − − = + − + 1 , 0 2 零点:z = 3 2 2 4 j j 极点: ,- ,- z = 1 1 2 ) ,为左边序列 z 所以 的收敛域为: X z( ) Re[ ]z j z Im[ ] 0 −3/ 4 j /2 − j /2 0.5 2024/10/21 6
Q2< 为双边序列 4jIm[=] Refz] 4jm[] 为右边序列 0.5 3/4 Re[z] i12 2024/10/21 >
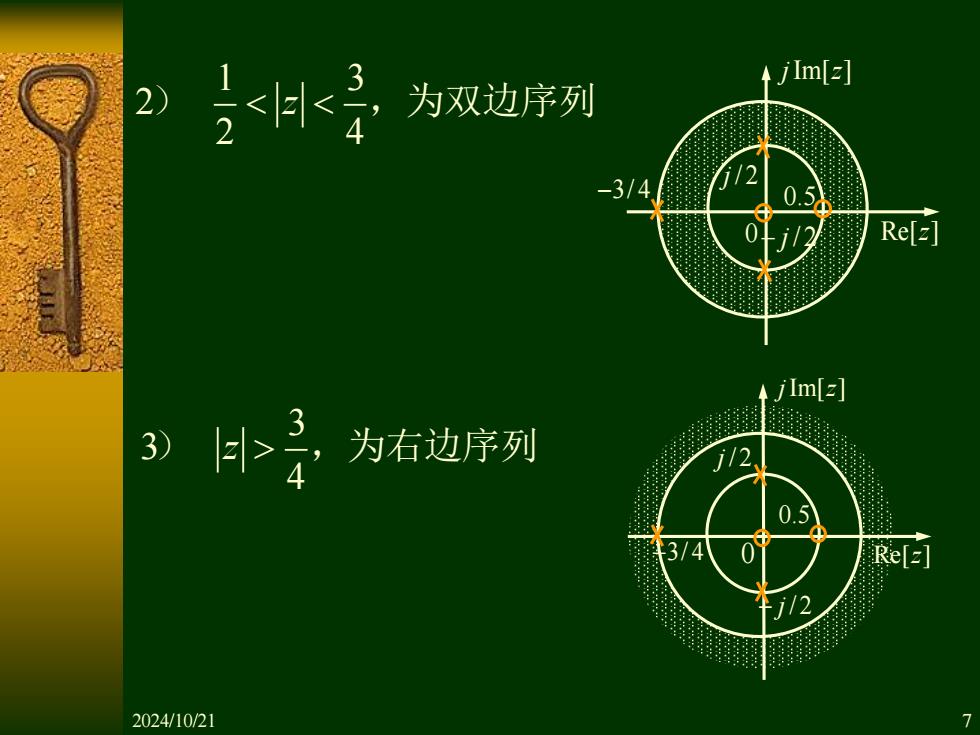
1 3 2 2 4 ) ,为双边序列 z 3 3 4 ) ,为右边序列 z Re[ ]z j z Im[ ] 0 −3/ 4 j /2− j /2 0.5 Re[ ]z j z Im[ ] −3/ 4 0 j /2 − j /2 0.5 2024/10/21 7

2-3用长除法,留数定理,部分分式法求以下X(2) 的z反变换 1) X(a) > -2 解:①长除法 X(z)= 2024/10/21 6
1 2 1 1 2 ( ) 1 1 4 z X z z − − − = − (1) 1 2 z 解:①长除法 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 2 2 z z z z − − − − − = = + − + 2-3 用长除法,留数定理,部分分式法求以下 的z反变换 X z( ) 1 2 1 1 2 ( ) 1 1 4 z X z z − − − = − 2024/10/21 8

由Roc判定x(n)是 右边序列,用长 )1 除法展成z的负 幂级数,分子分 母按z的降幂排 列 X(a)=1- 2 .x(n) (w 2024/10/2 9
1 1 2 1 2 1 1 1 1 2 1 1 1 2 4 1 1 2 4 1 2 z z z z z z − − − − − − + + − − − 1 1 1 2 1 2 4 z z − − 由Roc判定x(n)是 − + + 右边序列,用长 除法展成z的负 幂级数,分子分 母按z的降幂排 列 1 1 1 2 ( ) 1 2 4 X z z z − − = − + + 0 1 2 n n n z − = = − 1 ( ) ( ) 2 n x n u n = − 2024/10/21 9

②留数法 又1imX(z)=1即o处X(z)收敛 .x(n)为因果序列即x(n)=0,n<0 之1 当n≥0时,F(z)=X(z)z"-1= 1+-2 Z+ 2 2 F()在围线c内只有一个 jlm[z] 单阶极点:月 0.5 Re[z] 2024/10/21 10
1 : lim ( ) 1 ( ) 2 z ROC z X z X z → = 又 即 处 收敛 ②留数法 = x n x n n ( ) ( ) 0 0 为因果序列 即 , 当 n 0 时, 1 1 1 ( ) ( ) 1 1 1 2 2 n n n z z F z X z z z z − − − = = = + + 在围线c内只有一个 单阶极点 1 2 z = − F z( ) Re[ ]z j z Im[ ] 0 C −0.5 2024/10/21 10