
第三讲无线信源与信道 编码
第三讲 无线信源与信道 编码

三种编码技术 信源编码: 以提高通信有效性为目的的编码。 ■通常通过压缩信源的冗余度来实现。采用的一般方法是压缩每个 信源符号的平均比特数或信源的码率。即同样多的信息用较少的 码率传送,使单位时间内传送的平均信息量增加,从而提高通信 的有效性。 信道编码: ■是以提高信息传输的可靠性为目的的编码。 。通常通过增加信源的冗余度来实现。采用的一般方法是增大码率/ 带宽。与信源编码正好相反。 冬密码: ■是以提高通信系统的安全性为目的的编码。 通常通过加密和解密来实现。从信息论的观点出发“加密”可视 为增熵的过程.“解密”可视为减熵的过程。 Mobile Communication Theory
2 三种编码技术 v 信源编码: § 以提高通信有效性为目的的编码。 § 通常通过压缩信源的冗余度来实现。采用的一般方法是压缩每个 信源符号的平均比特数或信源的码率。即同样多的信息用较少的 码率传送,使单位时间内传送的平均信息量增加,从而提高通信 的有效性。 v 信道编码: § 是以提高信息传输的可靠性为目的的编码。 § 通常通过增加信源的冗余度来实现。采用的一般方法是增大码率/ 带宽。与信源编码正好相反。 v 密码: § 是以提高通信系统的安全性为目的的编码。 § 通常通过加密和解密来实现。从信息论的观点出发“加密”可视 为增熵的过程,“解密”可视为减熵的过程。 Mobile Communication Theory

内容 信源编码 冬分组码 冬卷积码 Turbo编码 Mobile Communication Theory
3 内容 v信源编码 v分组码 v卷积码 vTurbo编码 Mobile Communication Theory

基本概念 ”自信息量 对离散信源而言,信源x=[x,x,,x]的概率分布为P(x),P(x),…,P(x) ,则称 I(P(x,))=logz (1/P(x))=-logz(P(x,)) 为消息x,的自信息量,它具有随机变量的性质,但自信息量不能表示 信源总体的不定度。 信息熵 信息熵表示信源总体的不定度。它定义为信源信息的平均自信息量, 即 H()=E[I(P()] =-2P)e:Ps》 熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。 Mobile Communication Theory
4 基本概念 v 自信息量 对离散信源而言,信源 的概率分布为 ,则称 为消息 的自信息量,它具有随机变量的性质,但自信息量不能表示 信源总体的不定度。 v 信息熵 信息熵表示信源总体的不定度。它定义为信源信息的平均自信息量, 即 熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。 Mobile Communication Theory P x P x P x 1 2 , , , n I P x P x P x i i i log 1/ log 2 2 i x 2 1 log i n i i i H E I P x P x P x x x x x x 1 2 , , , n
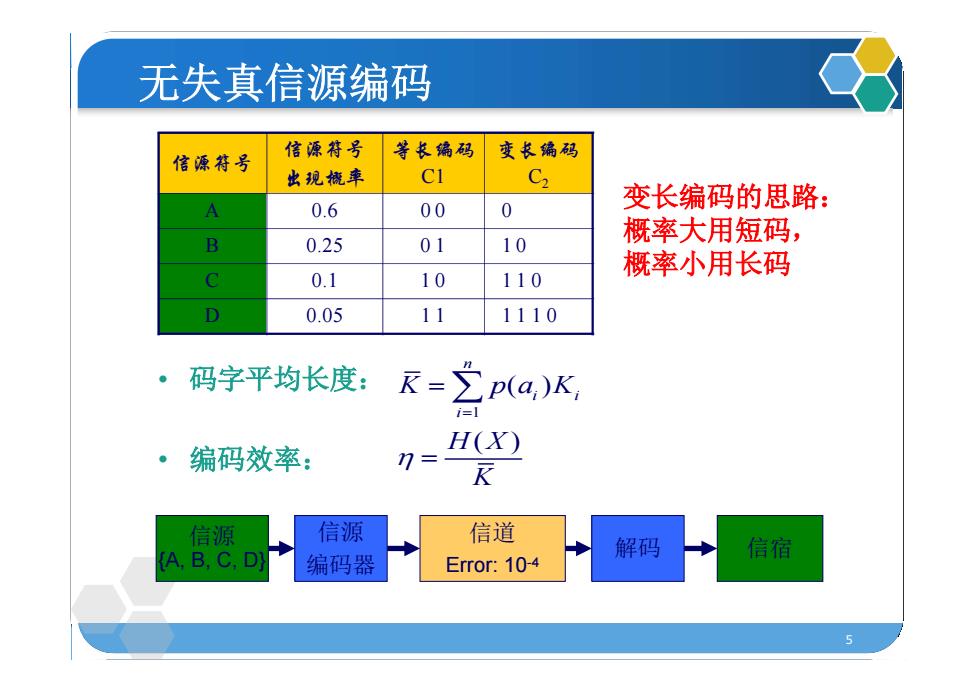
无失真信源编码 信源符号 信源符号 等长偏码 变长编码 出现概率 CI C2 A 0.6 00 0 变长编码的思路: B 0.25 01 10 概率大用短码, 概率小用长码 0.1 10 110 D 0.05 11 1110 。 码字平均长度:R-之p(a,)K, 编码效率: n=- (X) R 信源 信源 信道 (A,B,C,D) 解码 信宿 编码器 Error:10-4
5 信源 {A, B, C, D} 信源 编码器 信道 Error: 10-4 解码 信宿 无失真信源编码 信源符号 信源符号 出现概率 等长编码 C1 变长编码 C2 A 0.6 0 0 0 B 0.25 0 1 1 0 C 0.1 1 0 1 1 0 D 0.05 1 1 1 1 1 0 • 码字平均长度: • 编码效率: 1 ( ) ( ) n i i i K p a K H X K 变长编码的思路: 概率大用短码, 概率小用长码