
2019/9/6 任课教师:王磊 概率论讲义Chapt1 6.事件A与B互不相容(互斥) 实例抛掷一枚般子,现桌出现的点数 若事件A的出现必然导致事件B不出现,B “般子出现1点”互庄.“段子出现2点 出现也必然导致A不出现则称事件A与B互不相 容,即 的 ANB=AB=0. 实例抛将一枚硬币,“出现花面”与“出现字面 图示A与B互斥 是互不相容的两个事件. B ● ,事件A的对立事件 对立件与互斥率件的区别 设A表示“事件A出现”,则“事件A不出现 A、B互斥 4,B对立 称为事件A的对立事件或逆事件.记作入, 实例“股子出现1点”对立 .“子不出现1点 Bs A B-4s 图示A与B的对立 AB=0 AUB=S且AB= 互二 对立 若A与B互逆,则有AUB=S且AB=O。 ⊙0 事件间的运算规律设A,B,C为事件,则有 )交换律AUB=BUA,AB=B4. )A出现,BC不出现: 解(1)ABC (2)结合律(AUB)UC=AU(BUC). (AB)C=A(BC). A嘟出现C不出现: (2)ABC; (③)分配律 (3)三个事件至少有一个出现: (3)AUBUC (AUBOC=(400)U(BOC)=ACUBC (4)三个喜件都出现: (4)ABC: (AnB)UC=(AUC)n(BUC)=(AUCX(BUC) ⑤)三个事件都不出现 4德摩粮律:AU5,n五,AB-UE (不多于一个事件出现:(G)ARCUARCUARCUAR 0⊙① ④⊙@ 4
2019/9/6 4 6. 事件 A 与 B 互不相容 (互斥) 若事件 A 的出现必然导致事件 B 不出现, B 出现也必然导致 A不出现,则称事件 A与B互不相 容, 即 ABBA . 实例 抛掷一枚硬币, “出现花面” 与 “出现字面” 是互不相容的两个事件. “骰子出现1点” “骰子出现2点” 图示 A 与 B 互斥. S A B 互斥 实例 抛掷一枚骰子, 观察出现的点数 . 设 A 表示“事件 A 出现”, 则“事件 A 不出现” 称为事件 A 的对立事件或逆事件. 记作 A. 实例 “骰子出现1点” “骰子不出现1点” 图示 A 与 B 的对立. S B A 若 A 与 B 互逆,则有 BA S 且 AB . A 7. 事件 A 的对立事件 对立 对立事件与互斥事件的区别 S S A B A B A A、B 互斥 A、B 对立 AB BA S 且 AB 互 斥 对 立 事件间的运算规律 )1( 交换律 BAABABBA ., 结合律 )()2( CBACBA ),( )()()( , )3( BCACCBCACBA 分配律 (4)德摩根律 : , BABABABA . 设 BA C 为事件 ,,, 则有 AB C A BC).()( CBCACBCACBA ).)(()()()( 例1 设A,B,C 表示三个随机事件,试将下列事件 用A,B,C 表示出来. (1) A 出现 , B, C 不出现; (5) 三个事件都不出现; (2) A, B都出现, C 不出现; (3) 三个事件至少有一个出现; (4) 三个事件都出现; (6) 不多于一个事件出现; 解 CBA ;)1( CAB ;)2( )3( CBA ; ABC;)4( CBA ;)5( )6( CBACBACBACBA ; 任课教师:王磊 概率论讲义Chapt1
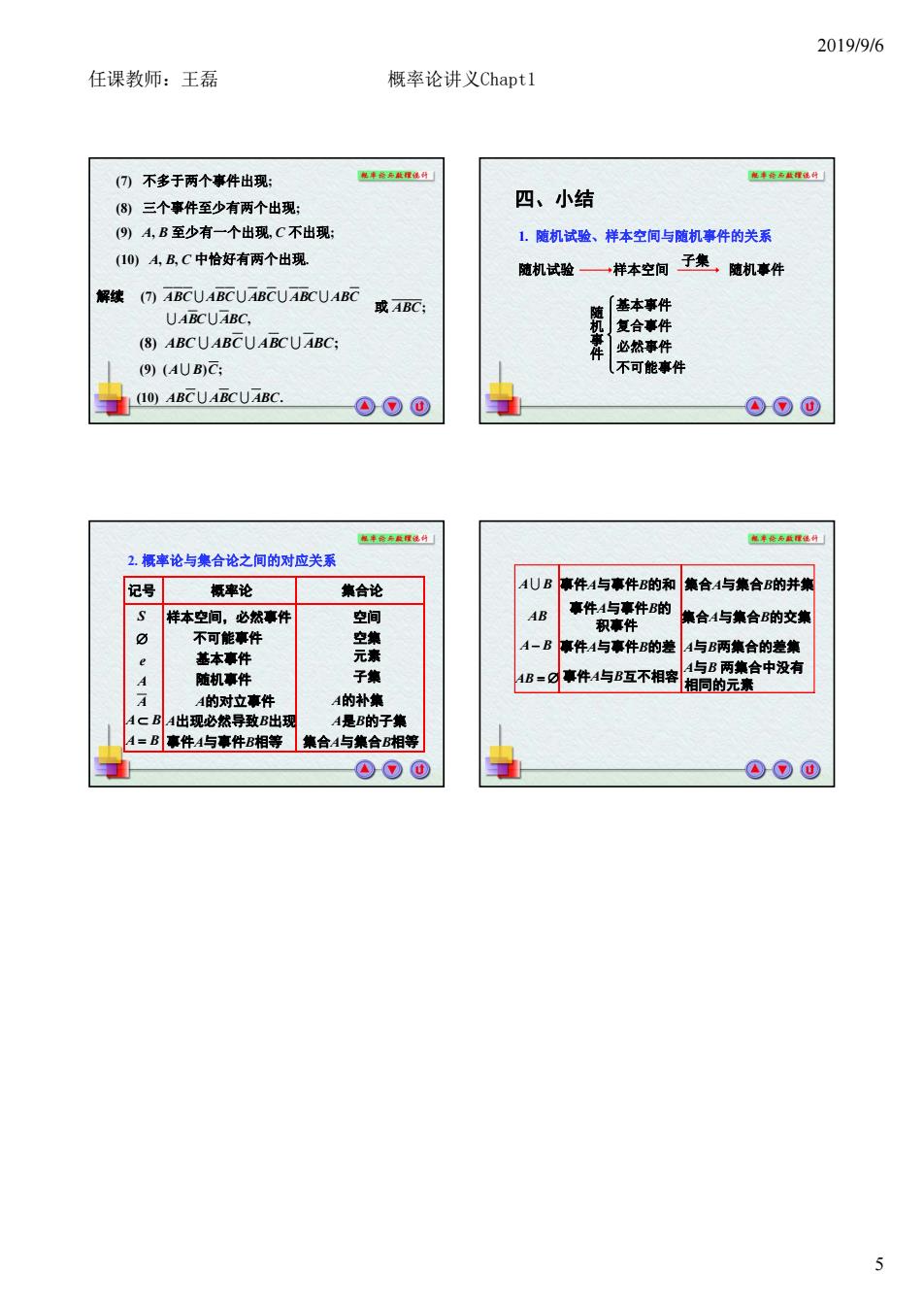
2019/9/6 任课教师:王磊 概率论讲义Chaptl (⑦刀不多于两个事件出现 (图)三个事件至少有两个出现: 四、小结 (9趴A,B至少有一个出现,C不出现 1.随机试验、样本空间与随机事件的关系 (10)4B,C中恰好有两个出现 随机试验一一样本空间子集随机事件 解()ABCUABCU BCUARCUABC 或ABC 「基本事件 复合事件 (8)ABCUABCUABCUABC: ()(AUB)C: (不可能事件 (10)ABCUABCUABC 2概率论与集合论之间的对应关系 记号 率论 集合论 AUB事件A与事件的和集合A与集合的并集 事件数气件的 合A与集合B的交 不可能 基本事件 A一B事件A与事件B的差A与B两集合的差集 城机惠件 子集 HB=事件A与B互不相容 1与B两集合中没有 相同的元素 A的对立事件 的补集 A出现必然导致B出现 A是B的子集 1=B事件A与事件相等集合A与集合相等 ⊙⊙⊙ 5
2019/9/6 5 (7) 不多于两个事件出现; (8) 三个事件至少有两个出现; (9) A, B 至少有一个出现, C 不出现; (10) A, B, C 中恰好有两个出现. )8( BCACBACABABC ; CBA ;)()9( )10( BCACBACAB . 或 ABC; , )7( BCACBA CABCBACBACBACBA 解续 随机试验 样本空间 子集 随机事件 随机事件 基本事件 必然事件 不可能事件 复合事件 四、小结 1. 随机试验、样本空间与随机事件的关系 2. 概率论与集合论之间的对应关系 记号 概率论 集合论 S 样本空间,必然事件 空间 不可能事件 空集 e 基本事件 元素 A 随机事件 子集 A A的对立事件 A的补集 BA A出现必然导致B出现 A是B的子集 BA 事件A与事件B相等 集合A与集合B相等 BA 事件A与事件B的差 A与B两集合的差集 AB 事件A与B互不相容 A与B 两集合中没有 相同的元素 BA 事件A与事件B的和 集合A与集合B的并集 AB 事件A与事件B的 积事件 集合A与集合B的交集 任课教师:王磊 概率论讲义Chapt1

2019/916 任课教师:王磊 概率论讲义Chapt1 第三节频率与概率 一、频率的定义与性质 1.定义 一、频率的定义与性质 二、概率的定义与性质 生的须数比值称为事件A发生的频率,并记 三、小结 成(40 2.性质 枚硬币抛掬5次、50次、500次客做 设A是随机试验E的任一事件,则 5 0s.0s: (2)fS=lf©= (③)若4,,,A是两两互不相容的事件,则 八4 UAU..-UA)=4)+f(4)+…+f(4为 ④⊙@ A)U 从上述数据可得 实验者 (山)须率有随机波动性,即对于同样的m,所得的 不一定相同: )抛币次数:较小时,频率∫的随机放动幅 240 202 度较大,但随n的增大,颜 )的大 ⊙⊙@ -④⊙@
2019/9/6 1 一、频率的定义与性质 二、概率的定义与性质 三、小结 第三节 频率与概率 ).( . , , , , Af A n n A n A n n n A A 成 生的频数 比值 称为事件 发生的频率 并记 次试验中 事件 发生的次数 称为事件 发 在相同的条件下 进行了 次试验 在这 1. 定义 一、频率的定义与性质 2. 性质 设 A 是随机试验 E 的任一事件, 则 f A ;1)(0)1( n f S f ;0)(,1)()2( ( ).()()() ,,,)3( , 21 1 2 21 k n n n k k AfAfAfAAAf AAA 若 是两两互不相容的事件 则 试验 序号 n 5 nH f 1 2 3 4 5 6 7 2 3 1 5 1 2 4 nH f n 50 22 25 21 25 24 18 27 nH n 500 251 249 256 247 251 262 258 0.4 0.6 0.2 1.0 0.2 0.4 0.8 0.44 0.50 0.42 0.48 0.36 0.54 f 0.502 0.498 0.512 0.494 0.524 0.516 0.50 0.502 实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做 7 遍, 观察正面出现的次数及频率. 在 处波动较大 2 1 波动最小 随n的增大, 频率 f 呈现出稳定性 在 处波动较小 2 1 从上述数据可得 (2) 抛硬币次数 n 较小时, 频率 f 的随机波动幅 度较大, 但随 n 的增大 , 频率 f 呈现出稳定性.即 当 n 逐渐增大时频率 f 总是在 0.5 附近摆动, 且 逐渐稳定于 0.5. (1) 频率有随机波动性,即对于同样的 n, 所得的 f 不一定相同; 实验者 德 摩根 蒲 丰 n nH f K 皮尔逊 K 皮尔逊 2048 1061 0.5181 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 f H)( n的增大 . 2 1 任课教师:王磊 概率论讲义Chapt1