
(3)将D1的第n+1行依次与上一行交换直至第1行;再将 所得行列式的第n+1行依次与上一行交换直至第2行::最后 将所得行列式的第n+1行与第n行交换,得 11.1 aa-1.a-n D.i=(-1)r-m-1a2(a-1)2.(a-n)2 a"(a-1)”.(a-n) 对右边的”十1阶行列式的列按前一方法处理,得 D1=(-1)型 (1)Ψ 1 .1 a-n a-n+1. a (a-n)2(a-n+1)2.a (a-n)"(a-n+1)”.a ,[a-+-)-a-n+)-D]= -》 an-1 b (4)D. 按第1行展开 d Cu-1 d 0 ·27
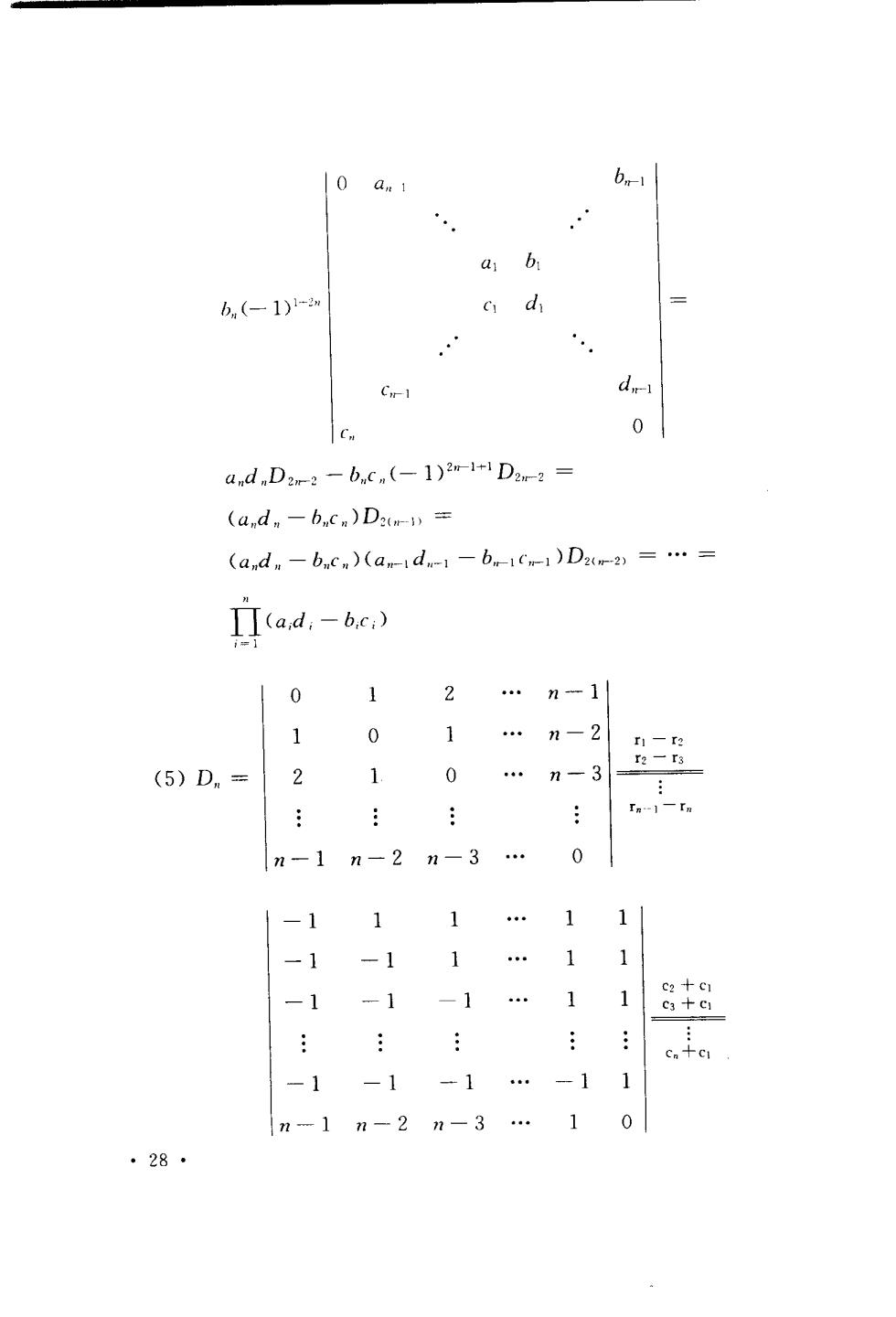
0 b b(-1)-2w d. d 0 andD2m2-bcn(-1)2w-11D2-2= (ad,-bc)D= (and-bc)(and-1-b1C1)D2m2)=.= Πa,d,-bc) 0 2 .n-1 0 -2 (5)Dn= 2 0 n-3 In-1-re n-1n-2n-3 1 ca +c 28
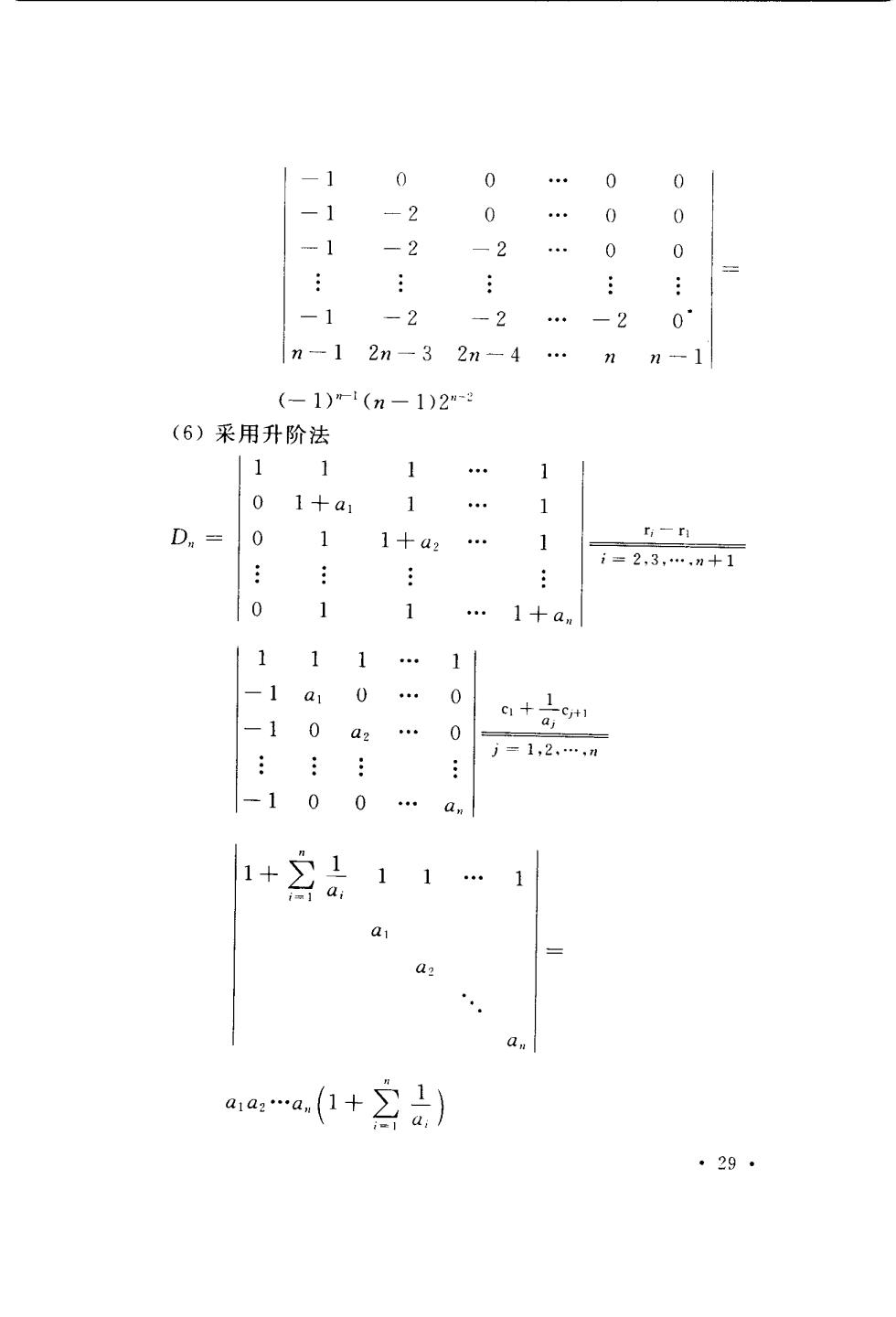
0 0 . 0 0 -2 0 0 1 -2 0 0 -1 -2 -2 0 n-12n-32n-4 (-1)-1(n-1)2- (6)采用升阶法 11 1 01+a1 D=0 11+a2 . 1 i=2,3,.”+1 0 1 1 .1十am 1 11. 1 -1a1 0 . 0 -10 0 + 方=1,2、.,m -1 0 0 a 1+乃1 1 1 a: a d? aa.a(1+】 ·29·

8.用克拉默法则解下列方程组: x1+x2+x3+x,=5 (1) x1+2x2-x3+4.x1=-2 2x1-3.x2-x3-5.x1=-2 3.x1+x2+2x3+11x4=0 5.r1+6.r2 =1 x1+5.x2+6x3 =0 (2) x2+5x3+6.x1 =0. x3+5.x1+6x5=0 x1+5.r3=1 解(1)可求得 111 1 11 0 0 0 12-14 /1 1 -2 3 D= 2-3-1-5 -5 -3 1312 11 -2-1 6 1-23 -5-3-7 142 -2-18 15 1 11 -2 2 -1 4 D1= =-142 -2 -3 -1 -5 70 1 2 11 11 5 1 1 1 -2 -1 4 D2= -284 2 -2 -1 -5 2 11 30·

1 1 1 1 2 -2 D3= 2 426 -3 -2 -5 3 1 0 11 11 1 1 5 2 -1 -2 D,= =142 -3-1 -2 312 0 所以 D x1= =1=号=2==3-号=-1 56000 15600 (2)D= 01560=665 00156 00015 16000 05600 D1= 0156 0 =1507 00156 10015 |51000 1 0600 D2= 00560 =-1145 00 156 0 015 ·31·