
(a-b)(a+b)b(a-b)(a-b) 2(a-b) a-br2÷(a-b) (a-):a+6 21 =(a-b)3 aray+b加ax+r by ay+be az+ba (2)D=ay axtbr ar+byb aztbr ar+by ax ar+by ay+be b ar+by ay+b r ay+bz az ®ayax十加axt s ax+by ay y bz az+br①s÷a b:bxar+by@s÷6 c2-bc3 Ix by ay+bz cs-ac: x ay zy z bx a y az r+b by ①c2÷a z ax y ②c3÷b c1-c2 xy之 (a3+6)y2x z r y ca-C a22a+14a+4 6a+9 (3)D9-c c3-2c b2b+14b+46b+9c4-3c c4- c22c+14c+46c+9 d 2d+14d+46d+9 ·22·

|a22a+126 b2b+126 =0 c22c+126 d2d+126 (4)由于行列式D中各列元素缺少3次幂的元素,在D中添 加3次幂的一行元素,再添加一列构成5阶范德蒙行列式 11111 a bcd x f(x)=a2 b c2 d2 x a b cd r 将f(x)按第5列展开得到x的4次多项式,且x3的系数为 A5=(-1)-5D=-D 而由教材例12得到 f(x)=(b-a)(c-a)(d-a)(x-a)(c-b)(d-b)X (x-b)(d-c)(x-c)(x-d)= [(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)]X (r-a)(x-b)(x-c)(x-d)= [(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)]x [x-(a+b+c+d)x3+.] 其中x3的系数为 -[(a-b)(a-c)(a-d)(b-c(b-d)(c-d](a+b+c+d) D=(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)x (a+b++d) (5)记左边的n阶行列式为D.,将其按第1列展开得 ·23·

x-1.0 0 0 .0 0 D.=x :+ 0 0 . x -1 1-10.00 -1.0 0 a(-1)-0 x .00 0 0. x-1 xD-1十an(-1)m1(-1)-1=D。-1x十am 于是Dn=D-1x十am=(D-2x十a-1)x十aa= Dn2x2+am-1x+am=.= D2x-2+a3x3+.十am-1x十am= x"+a1x-1十a2x"-2+.+ar1x+a 6.设n阶行列式D=det(a),把D上下翻转,或逆时针旋转 90°,或依副对角线翻转,依次得 a1wam D=::,D2=: at.an am.dIn D3=:: 证明:D,=D,=(-1)学D,D,=D. 证将D的第n行依次与上一行交换直至第1行;再将所得 行列式的第n行依次与上一行交换直至第2行;·;最后将所得行 ·24·

列式的第n行与第n-1行交换,得到行列式D,于是 D,=(1)-i-r-D=(-1)+D 对D2按对D的交换行的方法处理,即得D,于是 D,=-1)→D-(-1)→D 对D按对D的交换行的方法处理,得到行列式 am1.a D,==DI=D, am.am 故 D=(-1)4D,=(-1)+D, (-1)(-1)→D=D 7.计算下列各行列式(D。为k阶行列式): a 1 (1)Dn= 其中对角线上元素都是α,未写出的 a 元素都是0; (2)D.= :: aa.x a"(a-1)”.(a-n)" a-1(a-1)r1 (a-n)w1 (3)Dr1= a-1 1 1 . 1 ·25·
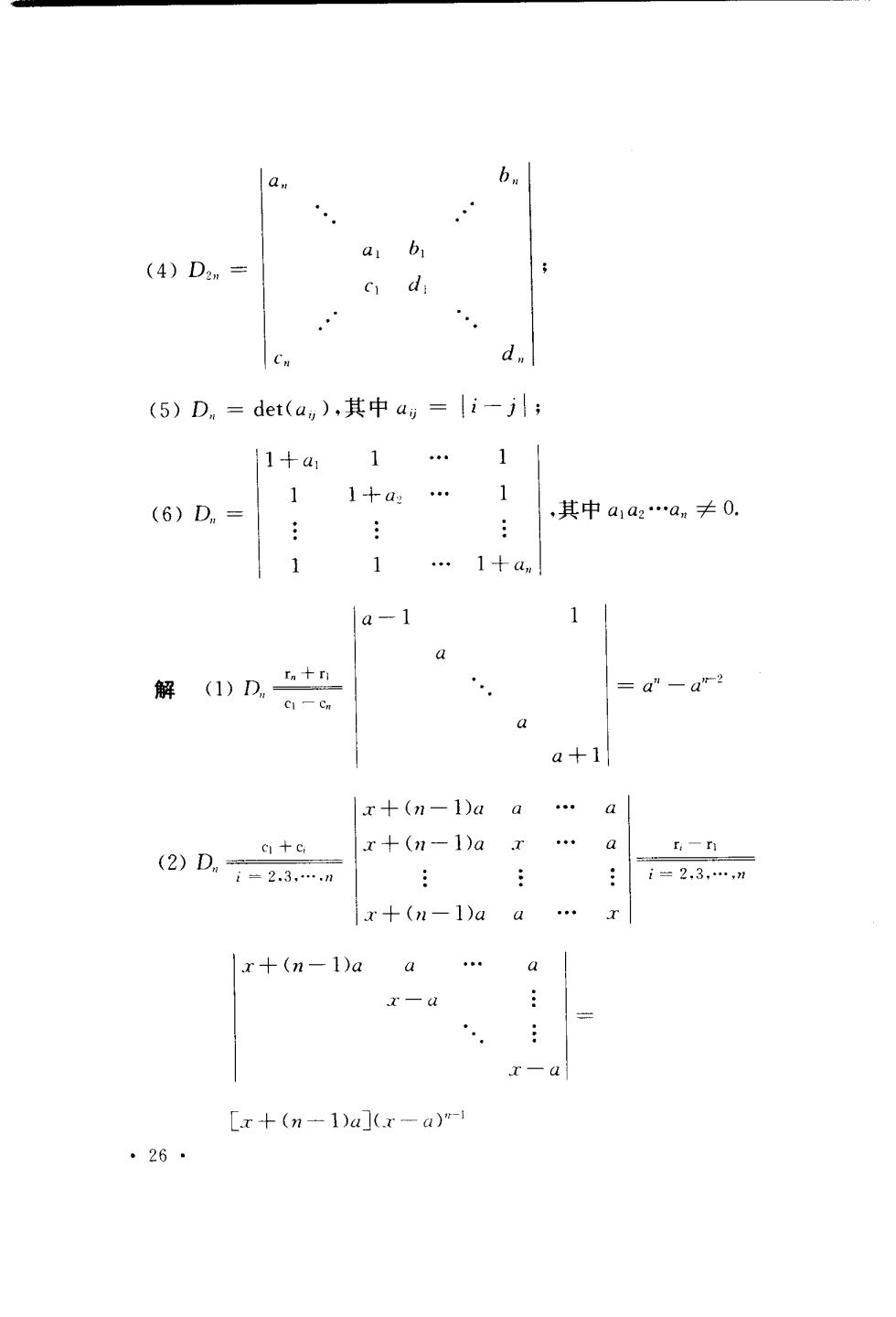
a. a b (4)D2m= d d, (5)D。=det(a,),其中a,=i-j 1+411.1 11-+a.1 (6)D.= 其中a1a2an≠0, 1 .1+an a-1 解)D,5+n =a"-a"2 cI-C a+1 x+(n-1)aa.a (2)D.=2.3n c十C, x+(n-1)a . a i=2.3,.,m x+(n-1)aa. |x+(n-1)aa a r-u r-a [x+(n-1)a](.x-a)"- ·26·