
7.Cramer法则 定理对于”个未知数个方程的线性方程组 a1x+a12x2+.+a1mxm=b a21x1+a22x2十.十a2mx。=b2 . a1x+an2x2+.十amtn=bn 如果系数行列式D=a,|≠0,则方程组有惟一解 西=号=骆,.,=丹 其中D,是把D中第j列换成常数项所得到的行列式,即 at.a1rba1ra1m . a2广-1ba2-1 . D,= (j=1,2,.,n) aa1.am广lb。anj-l.am 推论含n个未知数n个方程的齐次线性方程组 a11x1+a12x2+.十a1mxm=0 a21x1十a22+.+a2mxn=0 a1x1十am2x2十.+amxn=0 有非零解(即无穷多解)的充分必要条件是它的系数行列式 D=0. 注该推论的充分性由克拉默法则即得,而必要性由第三章的齐次线 性方程组有无穷多解的判定条件得到. 三、主要方法 除了较简单的行列式可以利用定义直接计算外,一般行列式 ·7·

计算的基本方法是: 方法一利用行列式的性质对行列式做恒等变形化为上 (下)三角行列式或次三角行列式,从而直接求得其值. 方法二利用按行(列)展开定理降低行列式的阶数.但在展 开之前往往先通过对行列式恒等变形,使得新行列式的某一行 (列)中有较多的零,再按该行(列)展开. 在计算行列式时,应根据行列式的特点和元素的规律性,采取 适当的次序和步骤来进行,因此,首先观察和研究行列式元素的规 律性是重要的. 计算行列式的常用技巧有三角化法、升阶(或加边)法、递推 法、数学归纳法等。 四、常考题型及考研典型题精解 例1~1计算n阶行列式 ar b az 62 D,= an-1 On b 分析对于形如/小的所谓两条线的行 列式,可直接展开降阶,再利用三角或次三角行列式的结果直接 ·8·
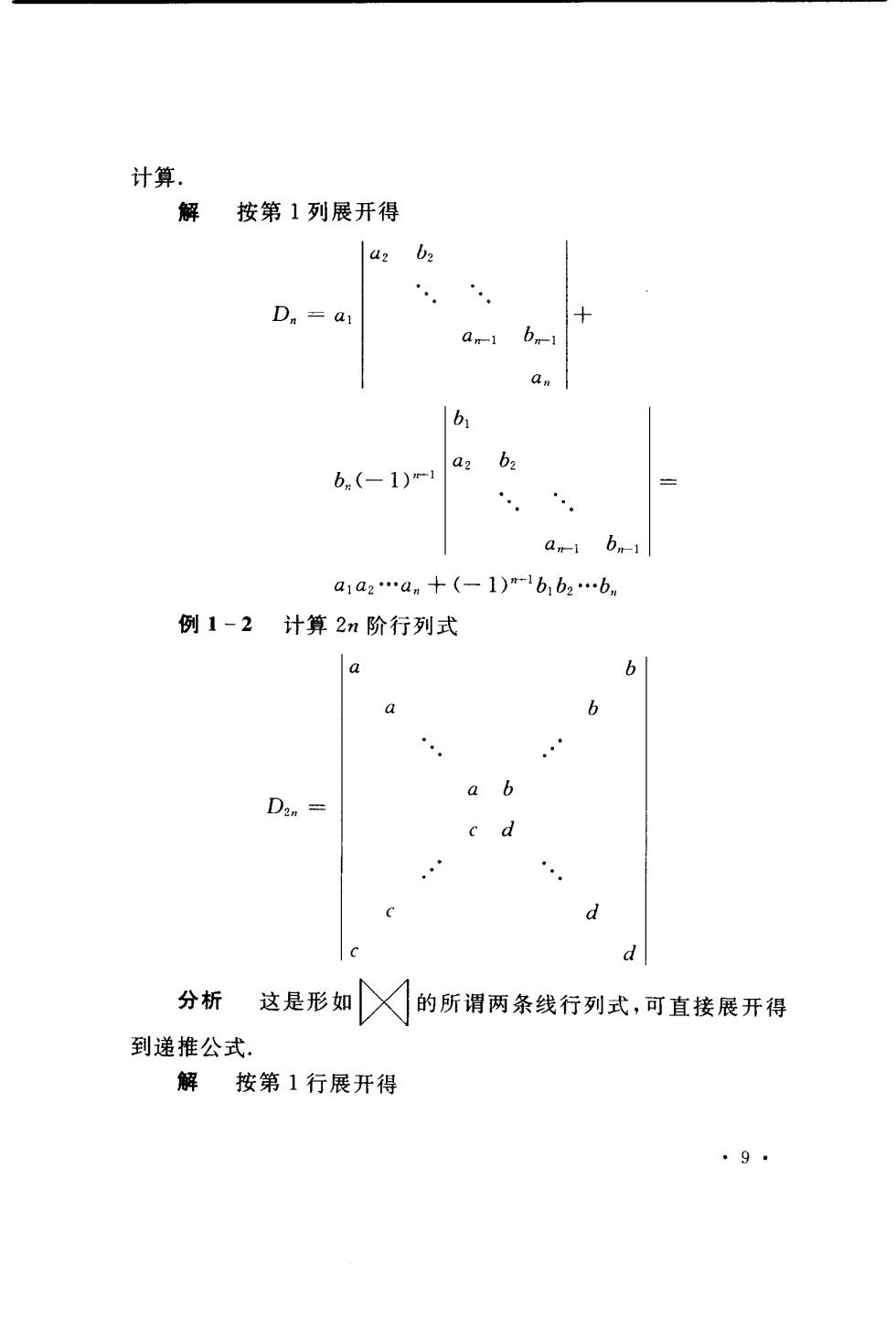
计算. 解按第1列展开得 D.=a an 6.(-1)m1a6 a1a2.an+(-1)m-1b1b2.bn 例1-2计算2n阶行列式 a 6 a a b D2= d 分析这是形如X的所谓两条线行列式,可直接展开得 到递推公式. 解按第1行展开得 ·9·

6 0 6 D2. d 0 0 a b(-1)1-2 d 0 ad x(-1)2r-11- (ad-b)D2 ·10·
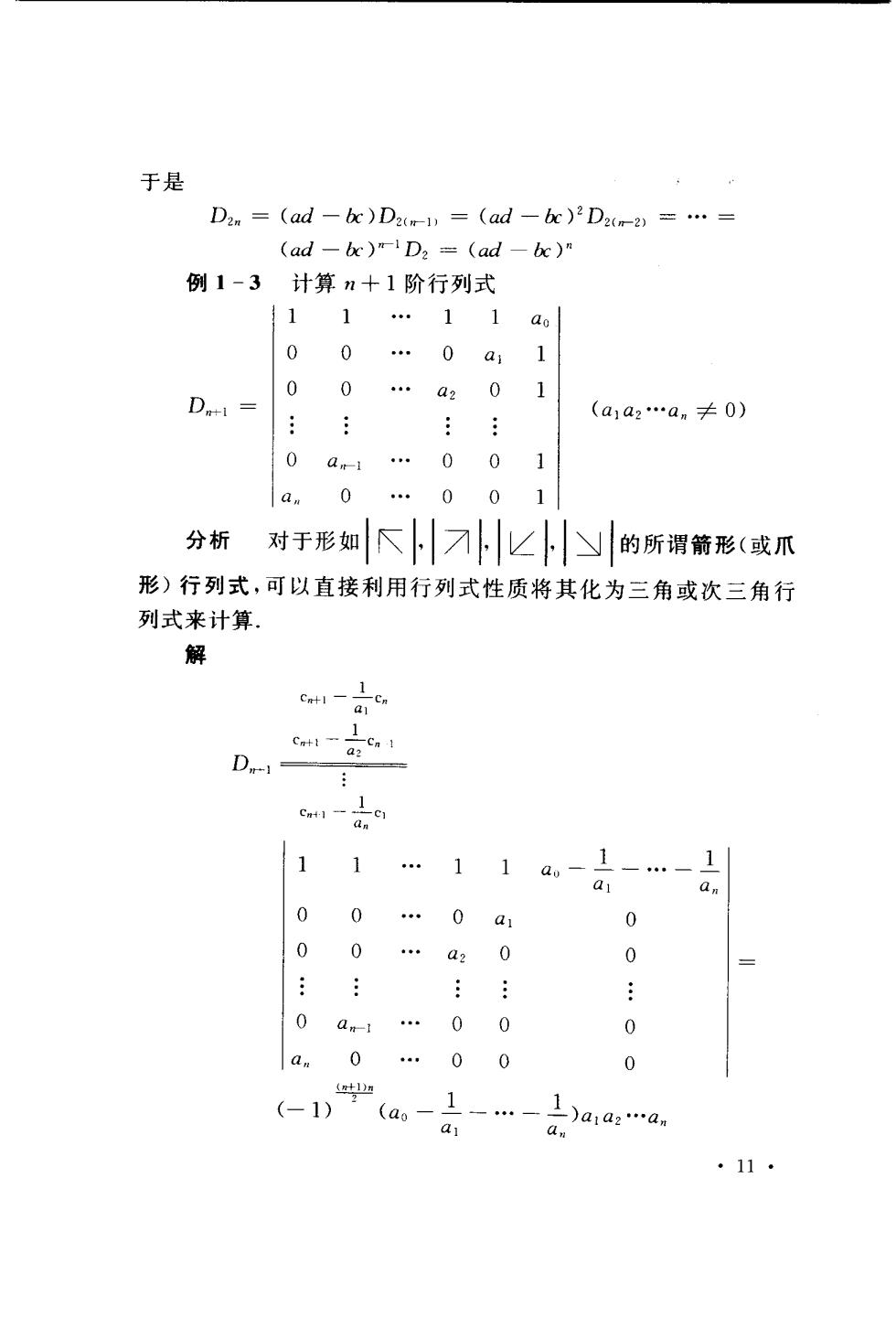
于是 Da =(ad-)Da(=(ad -b)'D=.= (ad-b)"D2 =(ad-be) 例1-3计算n十1阶行列式 11.11 0 0 0a1 00.a2 0 Dn+= (a1a2.an≠0) 0a1.001 a 0.001 分析 对于形如下川☑|ピy的所谓箭形(或爪 形)行列式,可以直接利用行列式性质将其化为三角或次三角行 列式来计算 解 Catl-a Cn 1 D-1 ca-c 11 . 11 ao 1 1 a 0 0.0a 0 0 0 0 0 0ag-1. 0 0 0 aa0.00 0 1) (ao- 1一. a )a1a2.an a ·11·