
阶行列式能熟练计算,而一般n阶行列式计算只要适当要求即可, 不必很难。 二、重要结论与公式 1.排列的性质 性质1交换排列中任意两个数,将改变排列的奇偶性 n个数1,2,.,n可以构成n!个不同的n阶排列,其中奇、偶排列 性质2 的个数各占罗 性质3 任一n阶排列p1p:“p。与标准排列12.n都可以经过一系列对 换互变,且所做对换的次数与排列p,p:“p,有相同的奇偶性. 2.对角线法则 对于2阶与3阶行列式,可以采用对角线法则来记它们所代 表的数: =a11a2-a12a2 a21ag anaza3+anazsan +anaz ase a13a22a31-a12421a33-a1a23a32 即实线上2个(3个)元素的乘积取正号,虚线上2个(3个)元素的 乘积取负号,再求其代数和就是行列式的值。 3.一些特殊行列式的值 (1)上(下)三角行列式等于其主对角线上元素的乘积,即 2
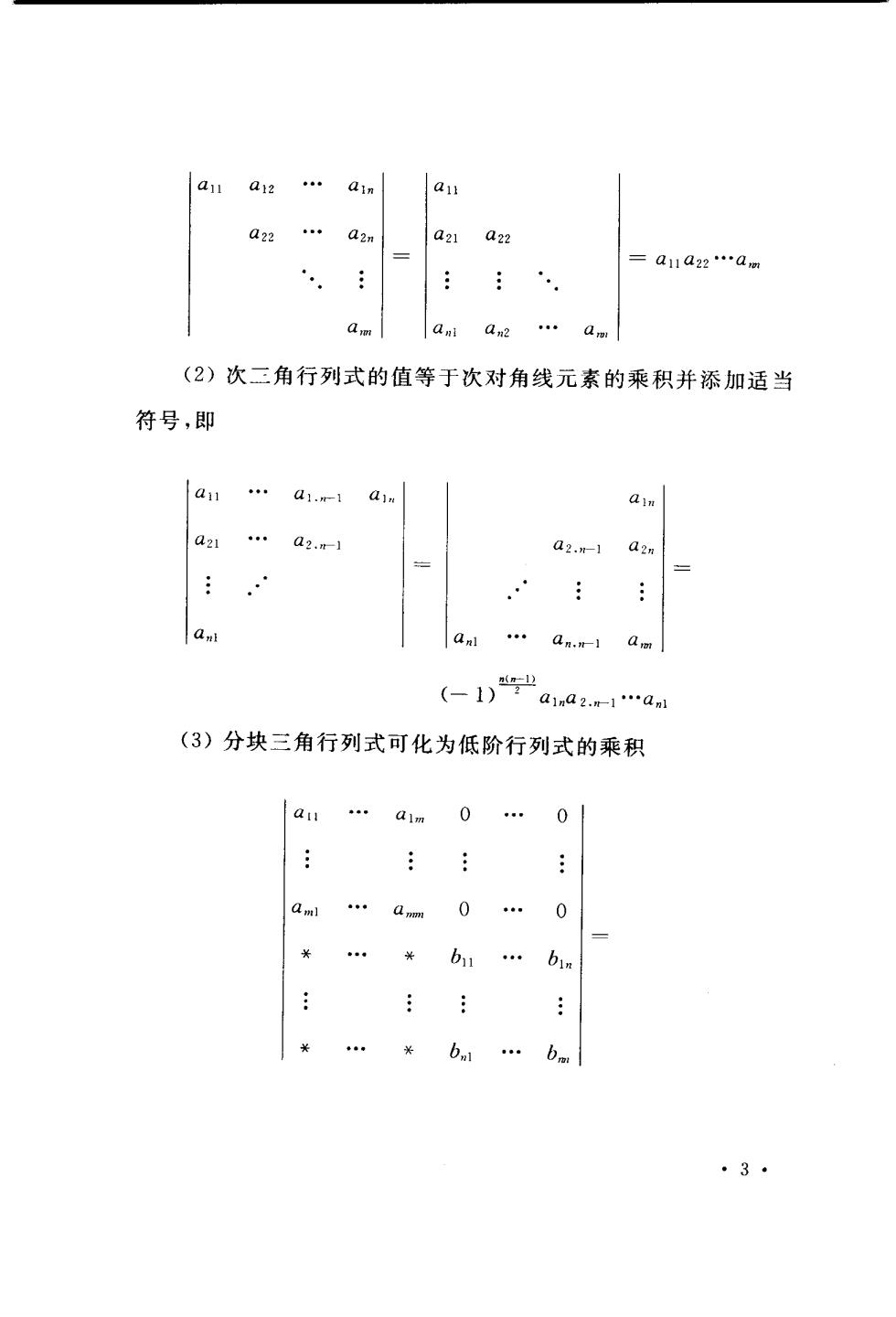
0 a22 a2 a11a22.a 0 a (2)次二角行列式的值等于次对角线元素的乘积并添加适当 符号,即 an . a a2-1 a2.1 azn a .a-1am (-1)→a1.a2r4.ai (3)分块三角行列式可化为低阶行列式的乘积 a11.a1m0.0| . 0.0 b1. bin bn1. ·3·
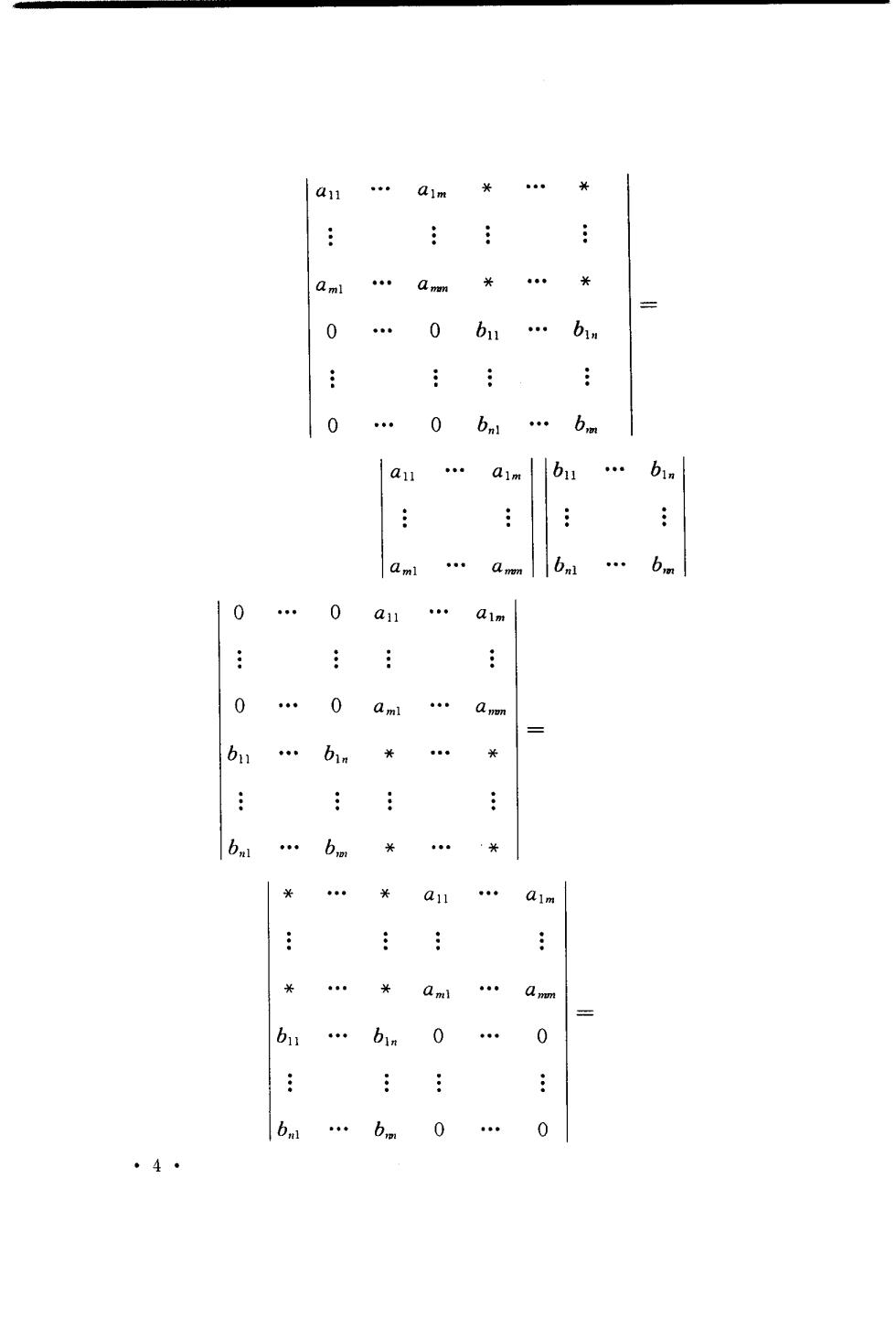
.· 0 . 0 . 6n 0 0 b 6. 0 a11 0 0 b .· . an .: 0 0 5 .b 0 . 4

(-1)m am .amb1 (4)范德蒙(Vandermonde)行列式直接套用公式 】 1.1 T2 . x Ⅱ(x:-x,)= x1x1.xW1 (x2-x1)(x3-x1).(xm-x1)X (x3-x2).(xm-x2)X .X (xn-工e1) 4.行列式的基本性质 性质1行列式与其转置行列式的值相等. 性质2行列式中某一行(列)如果有公因数k,则k可以提到 行列式符号外.特别地,若行列式中某行(列)元素全是零,则行列 式的值为零 性质3对换行列式中某两行(列)的位置,行列式的值改变 符号.特别地,如两行(列)元素对应相等或成比例,则行列式的值 是零 性质4如果行列式中某行(列)的每个元素都是两个数的 和,则这个行列式可以拆成两个行列式的和,这两个行列式分别以 ·5·

这两组数作为行(列),其余各行(列)与原行列式相同, 性质5把行列式某行(列)的倍加至另一行(列),行列式 的值不变.(在行列式计算中,往往先用这条性质作恒等变形,以期 简化计算.) 5.行列式按行(列)展开公式 a1a12.an 设D=a2:a:.an ,则 D=aA7十a2A2十.十amAm (i=1,2,.,n) D=aA+azAj++aA (j=1,2,.,n) 其中 a1a1 a1,41 . A=(←1)a-a-war ai-l.n a1l.ar1al1.a1 是a的代数余子式. 6.有关行列式的重要公式 行列式一行(列)元素与另一行(列)元素的代数余子式乘积 之和等于零,即 aaA1+a2A2十.+amA=0(i≠j) Q1A,十a2A2)+.十awAw=0(i≠j) 6*