Maximum Likelihood Estimation Pe(x) Pdata(x) Network Sample {x1,x2,....xm}from Pdata(x) We can compute Pe(xi) ??
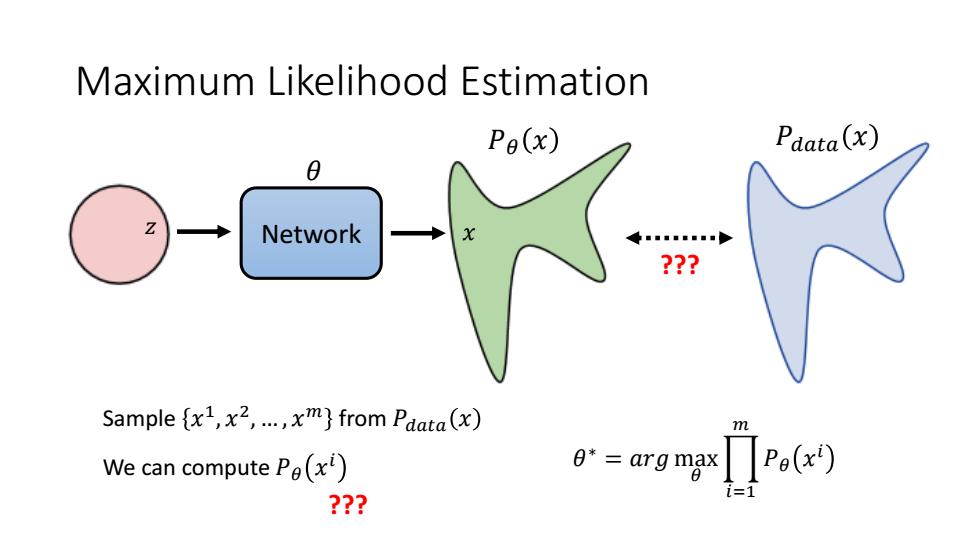
Maximum Likelihood Estimation Network 𝑧 𝑥 𝑃𝜃 𝑥 𝜃 𝑃𝑑𝑎𝑡𝑎 𝑥 Sample 𝑥 1 , 𝑥 2 , … , 𝑥 𝑚 from 𝑃𝑑𝑎𝑡𝑎 𝑥 We can compute 𝑃𝜃 𝑥 𝑖 𝜃 ∗ = 𝑎𝑟𝑔 max 𝜃 ෑ 𝑖=1 𝑚 𝑃𝜃 𝑥 𝑖 ??? ???

Sample x1,x2,...,xm}from Paata(x) m m o=arg mgx ΠP6=arg mxlog(xy m arg max logP(xargmx ExalogPo()] 台 (not related to arg max Paata(x)logPg(x)dx-Paata(x)logPaata(x)dx Pe(x) Difference between Pdata and Pe arg max Pata(x)P dx =arg min KL(PaatallPe) Maximum Likelihood Minimize KL Divergence
Sample 𝑥 1 , 𝑥 2 , … , 𝑥 𝑚 from 𝑃𝑑𝑎𝑡𝑎 𝑥 𝜃 ∗ = 𝑎𝑟𝑔 max 𝜃 ෑ 𝑖=1 𝑚 𝑃𝜃 𝑥 𝑖 = 𝑎𝑟𝑔 max 𝜃 𝑙𝑜𝑔ෑ 𝑖=1 𝑚 𝑃𝜃 𝑥 𝑖 = 𝑎𝑟𝑔 max 𝜃 𝑖=1 𝑚 𝑙𝑜𝑔𝑃𝜃 𝑥 𝑖 ≈ 𝑎𝑟𝑔 max 𝜃 𝐸𝑥~𝑃𝑑𝑎𝑡𝑎[𝑙𝑜𝑔𝑃𝜃 𝑥 ] = 𝑎𝑟𝑔 max 𝜃 න 𝑥 𝑃𝑑𝑎𝑡𝑎 𝑥 𝑙𝑜𝑔𝑃𝜃 𝑥 𝑑𝑥 − න 𝑥 𝑃𝑑𝑎𝑡𝑎 𝑥 𝑙𝑜𝑔𝑃𝑑𝑎𝑡𝑎 𝑥 𝑑𝑥 = 𝑎𝑟𝑔 min 𝜃 𝐾𝐿 𝑃𝑑𝑎𝑡𝑎||𝑃𝜃 = 𝑎𝑟𝑔 max 𝜃 න 𝑥 𝑃𝑑𝑎𝑡𝑎 𝑥 𝑙𝑜𝑔 𝑃𝜃 𝑥 𝑃𝑑𝑎𝑡𝑎 𝑥 𝑑𝑥 Maximum Likelihood = Minimize KL Divergence (not related to 𝜃) Difference between 𝑃𝑑𝑎𝑡𝑎 and 𝑃𝜃
VAE:Compute Pe(x) Pe(x) P9()= P(z)Pe(xIz)dz Network )- G(Z)=x G(z)+x G(z)=x 可能會幾乎都是0⑧ Network Pe(x|z) G(Z) exp(-G(z)-xll2) G(Z)=x Mean of Gaussian
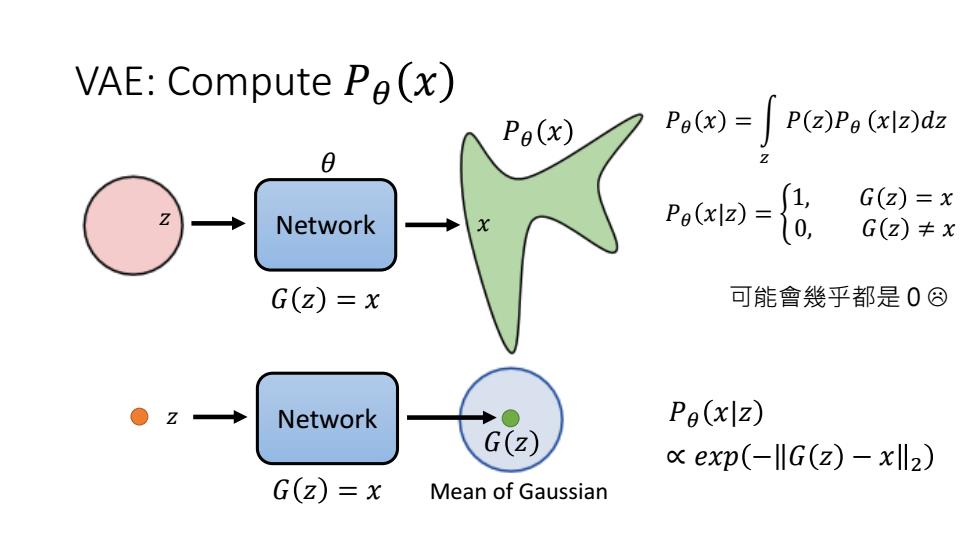
VAE: Compute 𝑃𝜃 𝑥 Network 𝑧 𝑥 𝑃𝜃 𝑥 𝜃 𝐺 𝑧 = 𝑥 𝑃𝜃 𝑥 = න 𝑧 𝑃 𝑧 𝑃𝜃 𝑥|𝑧 𝑑𝑧 𝑃𝜃 𝑥|𝑧 = ቊ 1, 𝐺 𝑧 = 𝑥 0, 𝐺 𝑧 ≠ 𝑥 可能會幾乎都是 0 𝑧 Network 𝐺 𝑧 = 𝑥 𝐺 𝑧 Mean of Gaussian ∝ 𝑒𝑥𝑝 − 𝐺 𝑧 − 𝑥 2 𝑃𝜃 𝑥|𝑧

VAE:Lower bound of logP(x) logPe(x)= q(zlx)logP(x)dz g(x)can be any distribution =4(zx )1og (》=awg P(z,x)q(zlx) q(zlx)P(zlx) dz q(zlx) ( + q(zlx)log dz P(zlx) ≥0 KL(q(zx)P(zx)) ≥∫eog dz =Eg()llog P(x,z) g(zx) lower bound Encoder
VAE: Lower bound of 𝑙𝑜𝑔𝑃 𝑥 𝑙𝑜𝑔𝑃𝜃 𝑥 = න 𝑧 𝑞 𝑧|𝑥 𝑙𝑜𝑔𝑃 𝑥 𝑑𝑧 𝑞 𝑧|𝑥 can be any distribution = න 𝑧 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑃 𝑧, 𝑥 𝑃 𝑧|𝑥 𝑑𝑧 = න 𝑧 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑃 𝑧, 𝑥 𝑞 𝑧|𝑥 𝑞 𝑧|𝑥 𝑃 𝑧|𝑥 𝑑𝑧 = න 𝑧 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑃 𝑧, 𝑥 𝑞 𝑧|𝑥 𝑑𝑧 + න 𝑧 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑞 𝑧|𝑥 𝑃 𝑧|𝑥 𝑑𝑧 𝐾𝐿 𝑞 𝑧|𝑥 ||𝑃 𝑧|𝑥 ≥ න 𝑧 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑃(𝑧,𝑥) 𝑞 𝑧|𝑥 𝑑𝑧 ≥ 0 = E𝑞 𝑧|𝑥 [𝑙𝑜𝑔 𝑙𝑜𝑤𝑒𝑟 𝑏𝑜𝑢𝑛𝑑 𝑃 𝑥, 𝑧 𝑞 𝑧|𝑥 ] Encoder
DDPM:Compute Pa(x) Denoise Denoise XT-1 Mean of Pe(xt-1lxt) Denoise G(x) Gaussian exp(-IIG(xt)-xt-1l2) Pe(xo)=P(xr)Po(xr-1lxr)..Pe(xt-1lxt)..Pe(xolxi)dx1:xr X1:XT
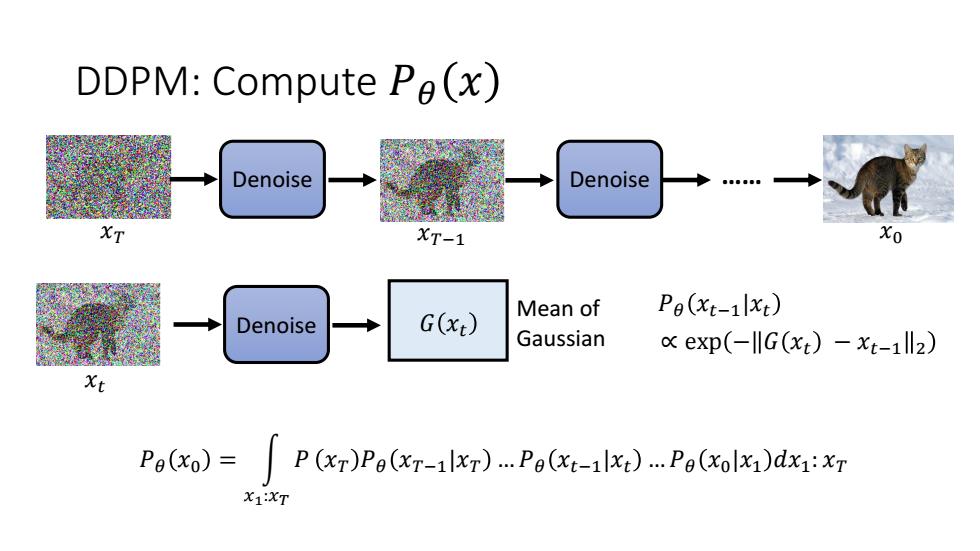
DDPM: Compute 𝑃𝜃 𝑥 Denoise Denoise …… 𝑥𝑇 𝑥𝑇−1 𝑥0 𝑃𝜃 𝑥0 = න 𝑥1:𝑥𝑇 𝑃 𝑥𝑇 𝑃𝜃 𝑥𝑇−1|𝑥𝑇 … 𝑃𝜃 𝑥𝑡−1|𝑥𝑡 … 𝑃𝜃 𝑥0|𝑥1 𝑑𝑥1: 𝑥𝑇 Denoise 𝑥𝑡 Mean of Gaussian 𝐺 𝑥𝑡 𝑃𝜃 𝑥𝑡−1|𝑥𝑡 ∝ exp − 𝐺 𝑥𝑡 − 𝑥𝑡−1 2