§21霞品煞的镜计解荐(换2) Chapter 2 The waoc junction and Scrodinger Eguation 2.波函数的统计解释 电子小孔衍射实验 D 0 电子源 光屏 电子单缝射实验
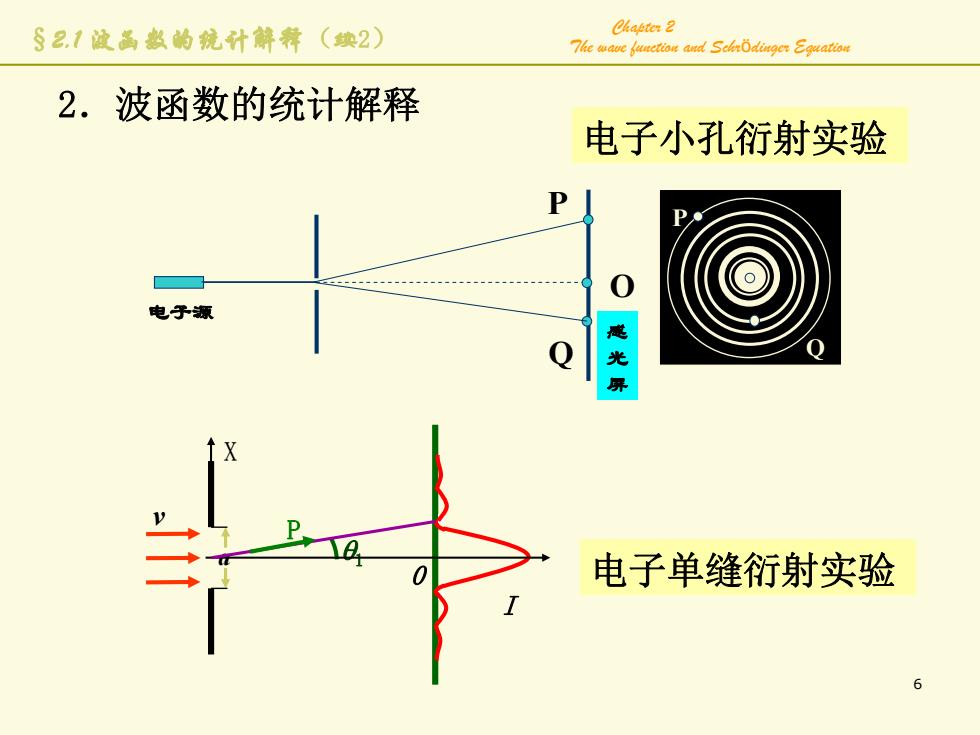
6 Chapter 2 The wave function and Schrödinger Equation a v I 0 θ1 X P 电子单缝衍射实验 2.波函数的统计解释 电子源 感 光 屏 P P Q Q O 电子小孔衍射实验 §2.1 波函数的统计解释(续2)
Chaster 2 A 电子射线发生擇 金隅结 电子衍射示意图
7 Chapter 2 The wave function and Schr ödinger Equation

§2.1波函数的统计解释(续3) Chapter 2 The waoc junction and Scrodinger Eguation 两种错误的看法 (1)波由粒子组成 如水波,声波,由物质的分子密度疏密变化而形 成的一种分布。 这种看法是与实验矛盾的,它不能解释长时间单 个电子衍射实验。 电子一个一个地通过小孔,但只要时间足够长, 底片上仍可呈现出衍射花纹。这说明电子的波动性 并不是许多电子在空间聚集在一起时才有的现象, 单个电子就具有波动性。 事实上,正是由于单个电子具有波动性,才能 理解氢原子(只含一个电子!)中电子运动的稳定 性以及能量量子化这样一些量子现象。 8
8 Chapter 2 The wave function and Schrödinger Equation ▲ 两种错误的看法 (1) 波由粒子组成 如水波,声波,由物质的分子密度疏密变化而形 成的一种分布。 这种看法是与实验矛盾的,它不能解释长时间单 个电子衍射实验。 电子一个一个地通过小孔,但只要时间足够长, 底片上仍可呈现出衍射花纹。这说明电子的波动性 并不是许多电子在空间聚集在一起时才有的现象, 单个电子就具有波动性。 事实上,正是由于单个电子具有波动性,才能 理解氢原子(只含一个电子!)中电子运动的稳定 性以及能量量子化这样一些量子现象。 §2.1 波函数的统计解释(续3)

§2.1波函数的统计解释(续4) Chapter 2 The waue junction and ScdingerEgeation 波由粒子组成的看法仅注意到了粒子性的一面,而抹 杀了粒子的波动性的一面,具有片面性。 (2)粒子由波组成 ·电子是波包。把电子波看成是电子的某种实际结构,是 维空间中连续分布的某种物质波包。因此呈现出干涉和 射等波动现象。波包的大小即电子的大小,波包的群速度 即电子的运动速度。 ·什么是波包?波包是各种波数(波长)平面波的迭加。 平面波描写自由粒子,其特点是充满整个空间,这是 因为平面波振幅与位置无关。如果粒子由波组成,那 么自由粒子将充满整个空间,这是没有意义的,与实 验事实相矛盾
9 Chapter 2 The wave function and Schrödinger Equation 波由粒子组成的看法仅注意到了粒子性的一面,而抹 杀了粒子的波动性的一面,具有片面性。 (2) 粒子由波组成 z电子是波包。把电子波看成是电子的某种实际结构,是三 维空间中连续分布的某种物质波包。因此呈现出干涉和衍 射等波动现象。波包的大小即电子的大小,波包的群速度 即电子的运动速度。 §2.1 波函数的统计解释(续4) z什么是波包?波包是各种波数(波长)平面波的迭加。 平面波描写自由粒子,其特点是充满整个空间,这是 因为平面波振幅与位置无关。如果粒子由波组成,那 么自由粒子将充满整个空间,这是没有意义的,与实 验事实相矛盾

§2.1波函数的统计解释(续5) Chapter 2 The wwue junction and Scndinger Eguation ·实验上观测到的电子,总是处于一个小区域内。 例如一个原子内的电子,其广延不会超过原子大小 ≈1A。 ·电子究竟是什么东西呢?是粒子?还是波? “ 电子既不是粒子也不是波”,既不是经典的粒 子也不是经典的波,但是我们也可以说,“电子既 是粒子也是波,它是粒子和波动二重性矛盾的统一。 这个波不再是经典概念的波,粒子也不是经典概念 中的粒子。 经典概念 1.有一定质量、电荷等“颗粒性”的属性; 中粒子意 2.有确定的运动轨道,每一时刻有一定 味着 位置和速度。 10
10 Chapter 2 The wave function and Schrödinger Equation z 实验上观测到的电子,总是处于一个小区域内。 例如一个原子内的电子,其广延不会超过原子大小 ≈1 。0A z电子究竟是什么东西呢?是粒子?还是波? “ 电子既不是粒子也不是波 ”,既不是经典的粒 子也不是经典的波,但是我们也可以说,“ 电子既 是粒子也是波,它是粒子和波动二重性矛盾的统一。” 这个波不再是经典概念的波,粒子也不是经典概念 中的粒子。 1.有一定质量、电荷等“颗粒性”的属性; 2.有确定的运动轨道,每一时刻有一定 位置和速度。 经典概念 中粒子意 味着 §2.1 波函数的统计解释(续5)