
(二)分类决策的制定 前面已选取了特征参数,把特征参数张成的多维空间称为特征空间。分类决策就是在特 征空间中用统计的方法把被识别对象归为某一类别.基本作法是在学习样本集的基础上确定 某个判快规则,使按这种判决规则对被甄别对象进行分类所造成的错误识别率最小或引起的 损失最少」 这里,我们的分类决策选取Fisher钱性判别法.即选取线性判别函数Ux,使得: U(x)-(E[U(x)-E:U(x)D2(D:[U(x)+D:U(x)D=max 1) 其中E与D,分别表示母体i的期望和方差运算,1,2. (1)式的含义是:物浩一个线性判别函数【《对样志讲行分类,使得平均出错概率最 小。即应在不同母体下 使 的 取值尽量分开。 具体地说 要使母体间的差异 (Ei(UE(UP相对于母体内的差异DU+DU1为最大.$ Ux=XX)'(E+E2'X 就可满足(山)其中了,为第类母体的均值矩阵的估计,∑:为第类母体的方差矩阵的估计.取 分类门槛值为: Um=Ua*X11-a)产灭) 其中0<a<1,本问题中两类样本的个数相等,可取a-1/2.若X)>,UX<U.则当 U>U就认为X取自母体1当U<U,就认为X取自母体2 用上面得出的4个主成分构成的特征组和此分类决策,对20个学习样本进行分类,能得 出正确的结果.但是,若取W=(,),求Y=X,以Y的3个分量作为特征参数向量,再 用Fisher线性判别法对20个学习样本进行分类,则第四个样本不能正确分类。 因此,得出分类的数学模型为: ,,求Y-,得出特征参数向量就是y的4个 列向量。其中X是反映20个学习样本的41个特征的随机向量, (2)分类决策:Fisher线性判别法. (三)分类模型的有效性考察 前面建立的分类数学模型对20个学习样本进行了正确分类.为了进一步考查分类模 型的有效性和可靠性,我们采用的方法是:预先留一部分学习样本不参加训练,然后用 分类决策棋型对其作预报,将预报成功率作为预报能力的指标。 每次取出一个学习样本,以其余学习样本作训练集,用分类决策棋型对取出的一个 样本作预报,同时对给出的后20种样本作预报。 结果见表4
(二)分类决策的制定 前面已选取了特征参数,把特征参数张成的多维空间称为特征空间.分类决策就是在特 征空间中用统计的方法把被识别对象归为某一类别.基本作法是在学习样本集的基础上确定 某个判决规则,使按这种判决规则对被甄别对象进行分类所造成的错误识别率最小或引起的 损失最少. 这里,我们的分类决策选取 Fisher 线性判别法.即选取线性判别函数 U(x),使得: U(x)={E1[U(x)]-E2[U(x)]}2 /{D1 [U(x)]+D2[U(x)]}=max (1) 其中 Ei 与 Di 分别表示母体 i 的期望和方差运算,i=1,2. (1)式的含义是:构造一个线性判别函数 U(x)对样本进行分类,使得平均出错概率最 小. 即应在不同母 体下,使 U(x)的取值尽 量分开.具体 地说,要使 母体间的差异 (E1(U(x))-E2(U(x)))2 相对于母体内的差异 D1[U(x)]+D2[U(x)] 为最大.取 U(x)=( X 1- X 2) T (∑1+∑2) -1X 就可满足(1).其中 X i 为第 i类母体的均值矩阵的估计,∑i为第 i类母体的方差矩阵的估计.取 分类门槛值为: U0=U(α* X 1+(1-α)* X 2) 其中 0<α<1,本问题中两类样本的个数相等,可取 α=1/2.若 U( X 1)>U0,U( X 2)<U0 , 则当 U(X)>U0., 就认为 X 取自母体 1;当 U(X)<U0, 就认为 X 取自母体 2. 用上面得出的 4 个主成分构成的特征组和此分类决策,对 20 个学习样本进行分类,能得 出正确的结果.但是,若取 W=(r1,r2,r3),求 Y=XW,以 Y 的 3 个分量作为特征参数向量,再 用 Fisher 线性判别法对 20 个学习样本进行分类,则第四个样本不能正确分类. 因此,得出分类的数学模型为: (1) 特征选取:取 W=(r1,r2,r3,r4),求 Y=XW,得出特征参数向量就是 Y 的 4 个 列向量.其中 X 是反映 20 个学习样本的 41 个特征的随机向量. (2) 分类决策:Fisher 线性判别法. (三)分类模型的有效性考察 前面建立的分类数学模型对 20 个学习样本进行了正确分类.为了进一步考查分类模 型的有效性和可靠性,我们采用的方法是:预先留一部分学习样本不参加训练,然后用 分类决策模型对其作预报,将预报成功率作为预报能力的指标. 每次取出一个学习样本,以其余学习样本作训练集,用分类决策模型对取出的一个 样本作预报,同时对给出的后 20 种样本作预报.结果见表 4.
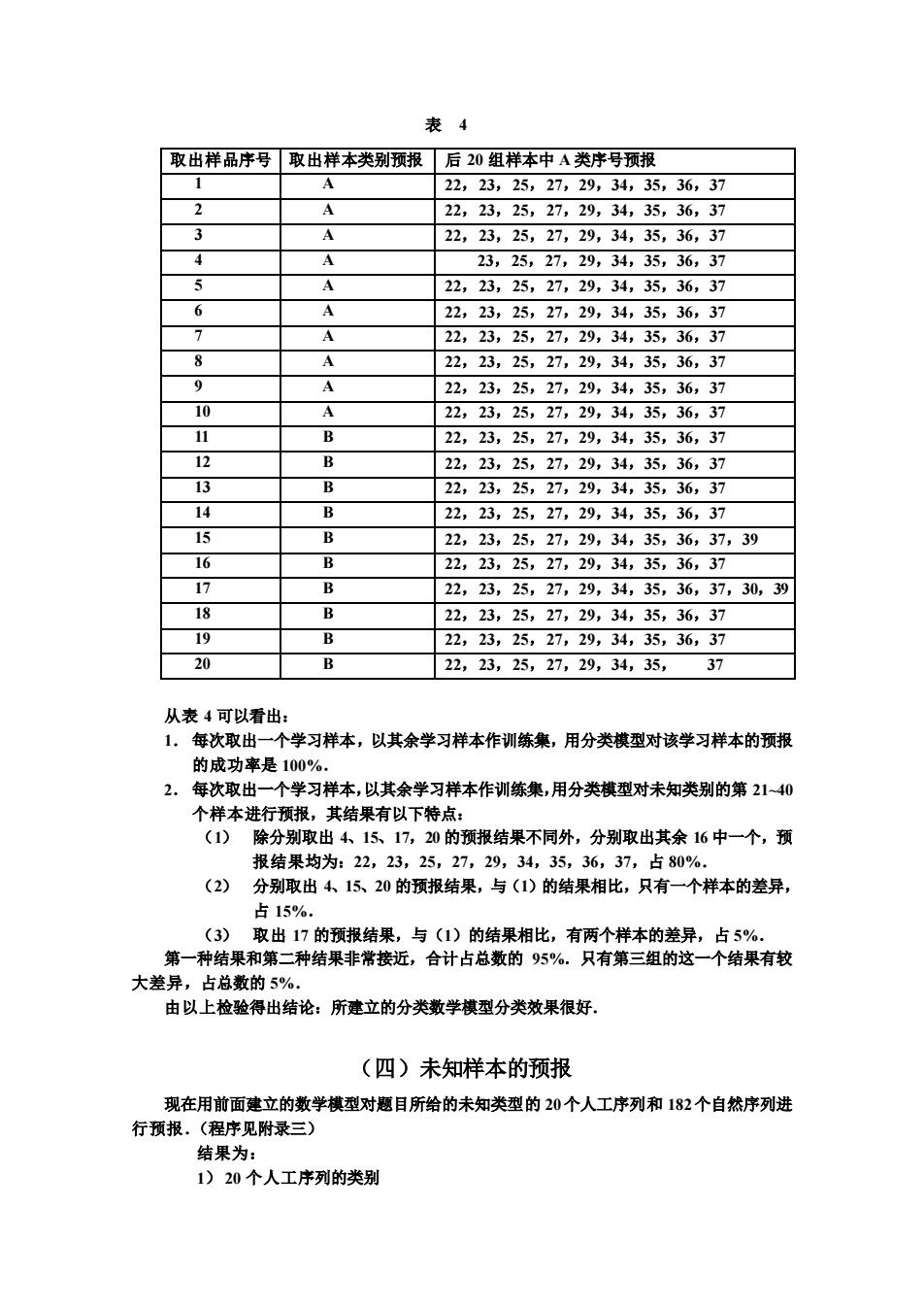
表4 取出样品序号取出样本类别预报后20组样本中A类序号预报 22,23,25,27,29,34,35,36,37 22,23,25,27,29,34,35,36,37 22,23,25,27,29,34,35,36,37 23,25,27,29,34,35,36,37 22,23,25,27,29,34,35,36,37 A 22,23.25,27,29,34,35,36,37 A 22,23,25,27,29,34,35,36,37 A 22,23,25,27,29,34,35,36,37 A 22,23,25,27,29,34,35,36,37 10 A 22,23.25,27,29,34,35,36,37 11 22,23,25,27,29,34,35,36,37 22,23,25,27,29,34,35,36,37 13 22,23,25,27,29,34,35,36,37 14 B 22.23.25.27.29.34.35.36.37 15 22,23,25,27,29,34,35,36,37,39 16 2223252729,34,35,30,3 17 B 22,23,25,27,29,34,35,36,37,30,39 18 22,23.2527,29,34.35.36.37 19 22,23,25,27,29,34,35, 36,37 20 B 22,23,25,27,29,34,35, 37 从表4可以看出 1. 每次取出 学习样本,以其余学习样本作训练集,用分类祺型对该学习样本的预报 的成功事是100%. 2.每次取出一个学习样本,以其余学习样本作训练集,用分类模型对未知类别的第2140 个样本进行预报,其结果有以下特点: (ω 除分别取出415、17,20的预报结果不同外,分别取出其余16中一个,预 报结果的 为:22,23,25, 27,29,34,35,36,37,占80% (2)分别取出415、20的预报结果,与(1)的结果相比,只有一个样本的差异, 占15%. (3)取出17的预报结果,与(1)的结果相比,有两个样本的差异,占5%. 第一种结果和第二种结果非常接近,合计占总数的95%。只有第三组的这一个结果有较 大差异,占总数的5% 由以上检验得出结论:所建立的分类数学模型分类效果很好 (四)未知样本的预报 现在用前面建立的数学模型对题目所给的未知类型的20个人工序列和182个自然序列进 行预报。(程序见附录三) 结果为: 1)20个人工序列的类别
表 4 从表 4 可以看出: 1. 每次取出一个学习样本,以其余学习样本作训练集,用分类模型对该学习样本的预报 的成功率是 100%. 2. 每次取出一个学习样本,以其余学习样本作训练集,用分类模型对未知类别的第 21~40 个样本进行预报,其结果有以下特点: (1) 除分别取出 4、15、17,20 的预报结果不同外,分别取出其余 16 中一个,预 报结果均为:22,23,25,27,29,34,35,36,37,占 80%. (2) 分别取出 4、15、20 的预报结果,与(1)的结果相比,只有一个样本的差异, 占 15%. (3) 取出 17 的预报结果,与(1)的结果相比,有两个样本的差异,占 5%. 第一种结果和第二种结果非常接近,合计占总数的 95%.只有第三组的这一个结果有较 大差异,占总数的 5%. 由以上检验得出结论:所建立的分类数学模型分类效果很好. (四)未知样本的预报 现在用前面建立的数学模型对题目所给的未知类型的 20个人工序列和 182个自然序列进 行预报.(程序见附录三) 结果为: 1) 20 个人工序列的类别 取出样品序号 取出样本类别预报 后 20 组样本中 A 类序号预报 1 A 22,23,25,27,29,34,35,36,37 2 A 22,23,25,27,29,34,35,36,37 3 A 22,23,25,27,29,34,35,36,37 4 A 23,25,27,29,34,35,36,37 5 A 22,23,25,27,29,34,35,36,37 6 A 22,23,25,27,29,34,35,36,37 7 A 22,23,25,27,29,34,35,36,37 8 A 22,23,25,27,29,34,35,36,37 9 A 22,23,25,27,29,34,35,36,37 10 A 22,23,25,27,29,34,35,36,37 11 B 22,23,25,27,29,34,35,36,37 12 B 22,23,25,27,29,34,35,36,37 13 B 22,23,25,27,29,34,35,36,37 14 B 22,23,25,27,29,34,35,36,37 15 B 22,23,25,27,29,34,35,36,37,39 16 B 22,23,25,27,29,34,35,36,37 17 B 22,23,25,27,29,34,35,36,37,30,39 18 B 22,23,25,27,29,34,35,36,37 19 B 22,23,25,27,29,34,35,36,37 20 B 22,23,25,27,29,34,35, 37

A类:22,23,25,27,29,34,35,36,37 B类:21、24、26、28、30、31、32、33、38、39、40 182个自然序列的类别 A类:(共142个)2,3,56,7,9,12,13,14,15,16,17,18,19,20, 21,22,23,24,25,26,28,30,31,33,34,35,36,37,38,39,40,42, 44,45,46,47,49,50,51,52,53,55,56,57,58,59,60,61,62,64 65.66.67.68. 69,773747,78,79,8082,83,84,85,87 89,91,93, 94, ,96,97,9899,10,101,103,104,105,106 107,108 109,111,112,113,114,115,117,118,120,121,122,123,124,125,127, 128,129,130,132,133,134,135,136,137,138,139,140,141,142,143, 145,146,147,148,149,151,152,153,154,155,156,158,167,168,171, 172,173.174.175,176.177,178.179.180,181 B类:(共40个) ,48,10,27,29,32, ,43 48,54,63, 70,72,75, 76,81,86,90,92,102,110,16,119,126131,144,150,157,159,160 161,162,163,164,165,166,169,170,182 四、模型的优缺点分析 优点: 1,针对“有人管理分类”问题,成功地建立解决这类难题的数学模型,并可立即运用 到实中 2.仅用4个特征参数即圆满解决了较为复杂的分类问题.而且棋型假设条件少,因而能 准确地反映实际情况,可靠性高。 3.采用模块化分析,逐渐深入,提高了准确性。 4卓出特征设合。免了在一些细节问上的纠靠 缺点 由于只考虑了DNA样本序列中1字符串、2字符串、3字符串出现的颜率作为特征, D、A序列的分类不一定与实际情况完全相符.(可以由科学家用物理的或化学的方法测定,作 为补充). 五、模型的改进方向及推广 模型的改进:因为棋型没考忠D八A序列的实际特性,当序列变得很多很长很复杂时,分 类的准确性会降低而不可用,因此应增加对DNA序列的生物特性的考忠. 棋型的推广:该模型对一般的“有人管理分类”问愿的求解有重要意义对研究DNA序 列的规律性和结构提供了一种有效的分类模型。对人类基因组的研究有现实意义,有利于加 快科研步伐
A 类:22,23,25,27,29,34,35,36,37 B 类:21、24、26、28、30、31、32、33、38、39、40 2) 182 个自然序列的类别 A 类:(共 142 个)2,3,5,6,7,9,11,12,13,14,15,16,17,18,19,20, 21,22,23,24,25,26,28,30,31,33,34,35,36,37,38,39,40,42, 44,45,46,47,49,50,51,52,53,55,56,57,58,59,60,61,62,64, 65,66,67,68,69,71,73,74,77,78,79,80,82,83,84,85,87,88, 89,91,93,94,95,96,97,98,99,100,101,103,104,105,106,107,108, 109,111,112,113,114,115,117,118,120,121,122,123,124,125,127, 128,129,130,132,133,134,135,136,137,138,139,140,141,142,143, 145,146,147,148,149,151,152,153,154,155,156,158,167,168,171, 172,173,174,175,176,177,178,179,180,181 B 类:(共 40 个)1,4,8,10,27,29,32,41,43,48,54,63,70,72,75, 76,81,86,90,92,102,110,116,119,126,131,144,150,157,159,160, 161,162,163,164,165,166,169,170,182 四、模型的优缺点分析 优点: 1. 针对`“有人管理分类”问题,成功地建立解决这类难题的数学模型,并可立即运用 到实践中去. 2. 仅用 4 个特征参数即圆满解决了较为复杂的分类问题.而且模型假设条件少,因而能 准确地反映实际情况,可靠性高. 3. 采用模块化分析,逐渐深入,提高了准确性. 4. 突出特征,假设合理,避免了在一些细节问题上的纠缠. 缺点: 由于只考虑了 DNA 样本序列中 1 字符串、2 字符串、3 字符串出现的频率作为特征, DNA 序列的分类不一定与实际情况完全相符.(可以由科学家用物理的或化学的方法测定,作 为补充). 五、模型的改进方向及推广 模型的改进:因为模型没考虑 DNA 序列的实际特性,当序列变得很多很长很复杂时,分 类的准确性会降低而不可用,因此应增加对 DNA 序列的生物特性的考虑. 模型的推广:该模型对一般的“有人管理分类”问题的求解有重要意义.对研究 DNA 序 列的规律性和结构提供了一种有效的分类模型.对人类基因组的研究有现实意义,有利于加 快科研步伐.