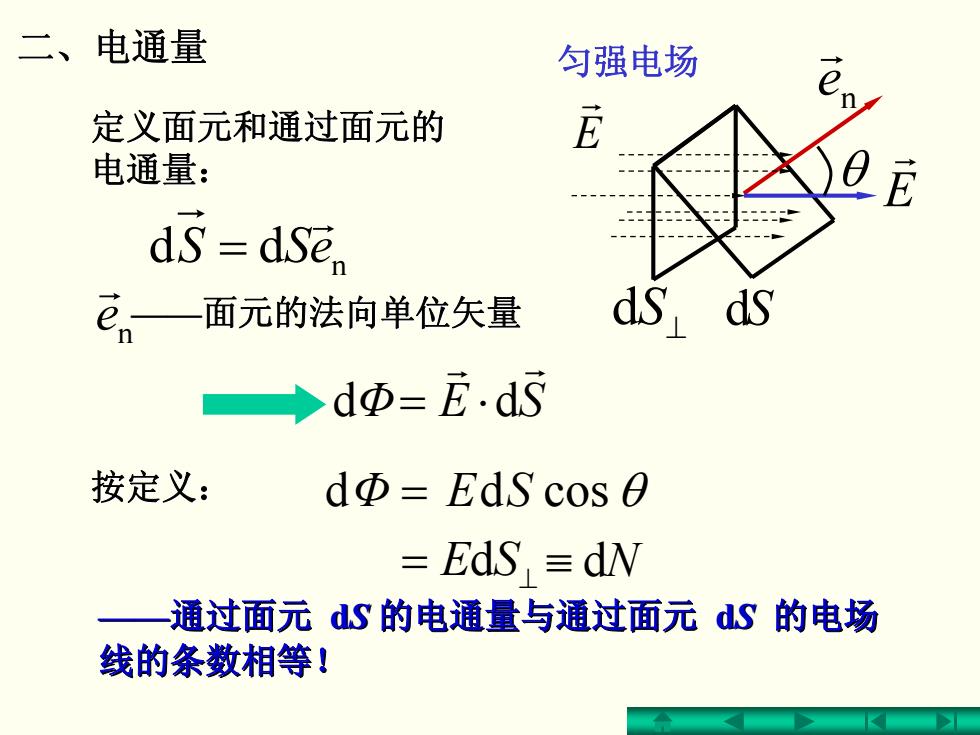
二、电通量 匀强电场 定义面元和通过面元的 电通量: ds dse, en— 面元的法向单位矢量 ds, ds →dΦ=E.d5 按定义: dΦ=EdS cos 0 EdS dN 通过面元dS的电通量与通过面元dS的电场 线的条数相等!
dS n e r r E = dSE ⊥ E r dd n eSS r = Φ = SE cosdd θ Φ SE r r ⋅= dd 二、电通量 匀强电场 θ 定义面元和通过面元的 定义面元和通过面元的 电通量: n e r ——面元的法向单位矢量 面元的法向单位矢量 dS⊥ ≡ dN ——通过面元 dS 的电通量与通过面元 的电通量与通过面元 dS 的电场 线的条数相等! 线的条数相等! 按定义:

通过任意曲面的电通量如何计算? 按数学的办法:把曲面切割成无穷多个面元,每 面元处可视为匀强电场 dΦ=E.dS 对曲面S总的电通量 -[E.ds
∫ Φ= dΦ 按数学的办法:把曲面切割成无穷多个面元,每 一面元处可视为匀强电场 ∫ ⋅= S SE 通过任意曲面的电通量如何计算? r r d 对曲面 S 总的电通量 S Φ SE dS r r ⋅= dd Ev
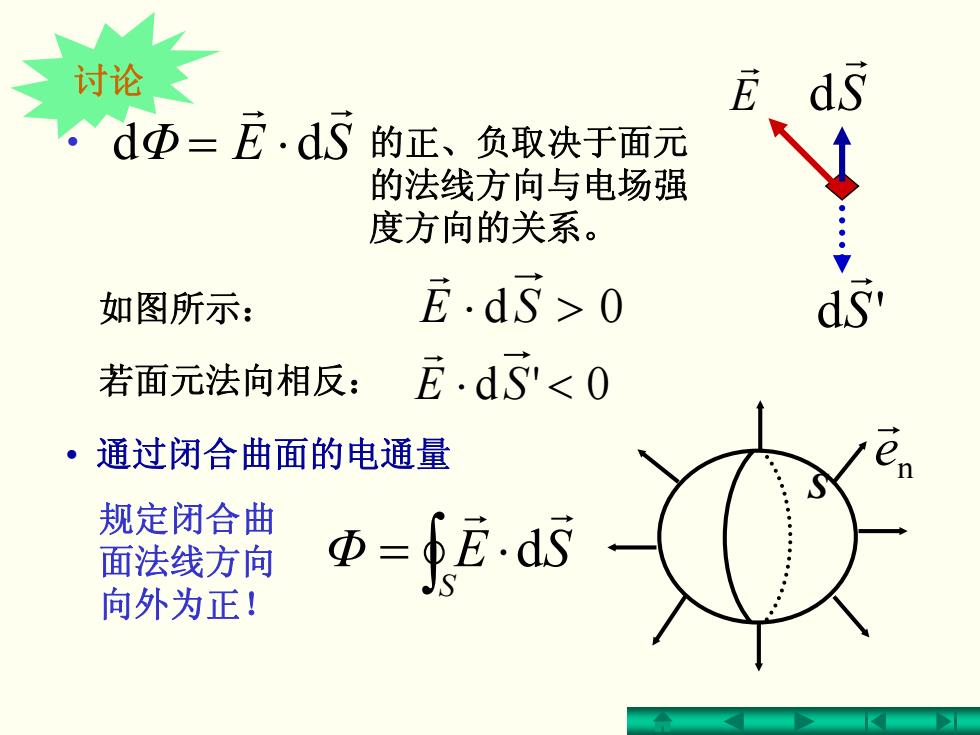
讨论 E ds 。dΦ=龙.d5的正、负取决于面元 的法线方向与电场强 度方向的关系。 如图所示: E.d5>0 若面元法向相反: E.d5<0 ·通过闭合曲面的电通量 规定闭合曲 面法线方向 -fE-as 向外为正!
• 通过闭合曲面的电通量 ∫ ⋅= S Φ SEr r d Φ SE r r • ⋅= dd 的正、负取决于面元 的法线方向与电场强 度方向的关系。 S r d rE 如图所示: SE >⋅ 0d r 若面元法向相反: SE <⋅ 0'd r S 规定闭合曲 面法线方向 向外为正! n e r S'd r 讨论
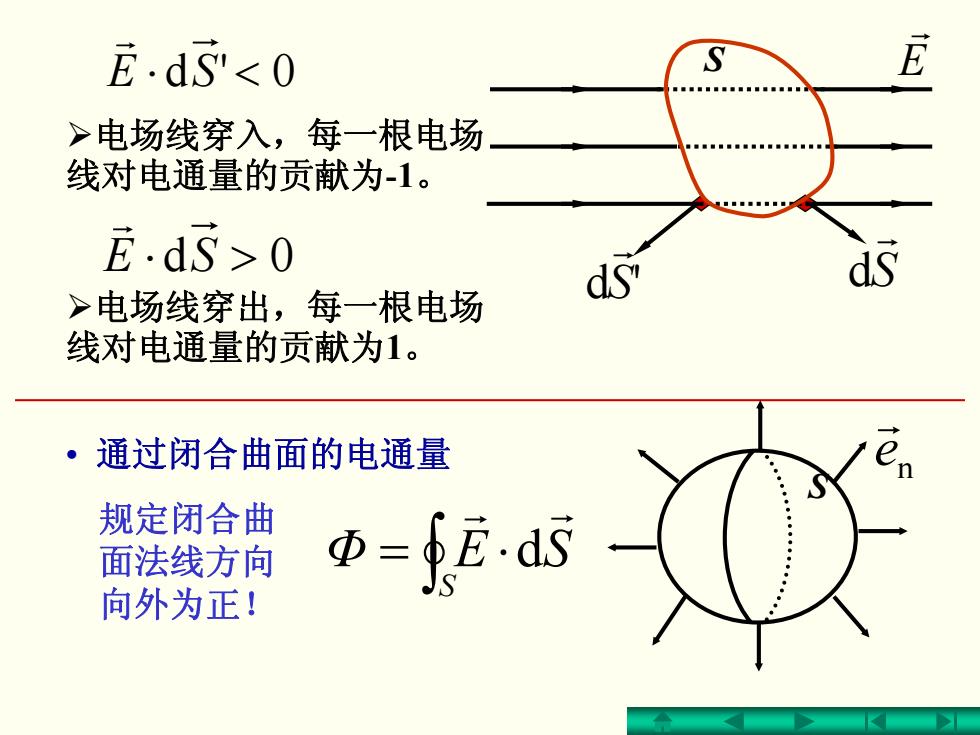
E.ds<o S >电场线穿入,每一根电场 线对电通量的贡献为-1。 E.d5>0 dS" >电场线穿出,每一根电场 线对电通量的贡献为1。 通过闭合曲面的电通量 规定闭合曲 面法线方向 向外为正! -fE-d5
S'd r S r d SE >⋅ 0d r SE <⋅ 0'd r ¾电场线穿入,每一根电场 线对电通量的贡献为-1。 ¾电场线穿出,每一根电场 线对电通量的贡献为1。 • 通过闭合曲面的电通量 ∫ ⋅= S Φ SEr r d S 规定闭合曲 面法线方向 向外为正! n e r E r S