
牛顿法的变种 牛顿法只用到了一阶导数的信息 -注:二次收敛的分析也可以在只假设f'是c-Lipschitz的情况下进行 - 如果使用更高阶的导数呢?例如,并不只是考虑切线,而是在局部做一个二 次曲线的近似 牛顿法更容易推广到高维,可以解决多变量的求根问题/最优化问题 然而导数可能并不容易求解:割线法(secant method),quasi--newton method -Secant method:)(1.2. f(xk)-f(xk-1) -Convergence rate of Secant method:1.618 quasi-newton method非常常见的一个实现是Broyden-Fletcher--Goldfarb-Shanno (BFGS)算法 ·现实中,往往会结合二分法和牛顿/割线法(如Dekker/Brent方法) -二分法可以保证全局收敛 一 牛顿/割线法可以保证在足够接近解的时候,更快速地收敛到需要的精度 9
牛顿法的变种 • 牛顿法只用到了一阶导数的信息 – 注:二次收敛的分析也可以在只假设�' 是C-Lipschitz的情况下进行 – 如果使用更高阶的导数呢?例如,并不只是考虑切线,而是在局部做一个二 次曲线的近似 • 牛顿法更容易推广到高维,可以解决多变量的求根问题/最优化问题 • 然而导数可能并不容易求解:割线法 (secant method),quasi-newton method – Secant method: �"#$ = �" − & '" '"('"#$ & '" (& '"#$ , � = 1,2, … – Convergence rate of Secant method: $# ) * ≈ 1.618 – quasi-newton method非常常见的一个实现是Broyden-Fletcher-Goldfarb-Shanno (BFGS)算法 • 现实中,往往会结合二分法和牛顿/割线法(如Dekker/Brent方法) – 二分法可以保证全局收敛 – 牛顿/割线法可以保证在足够接近解的时候,更快速地收敛到需要的精度 9
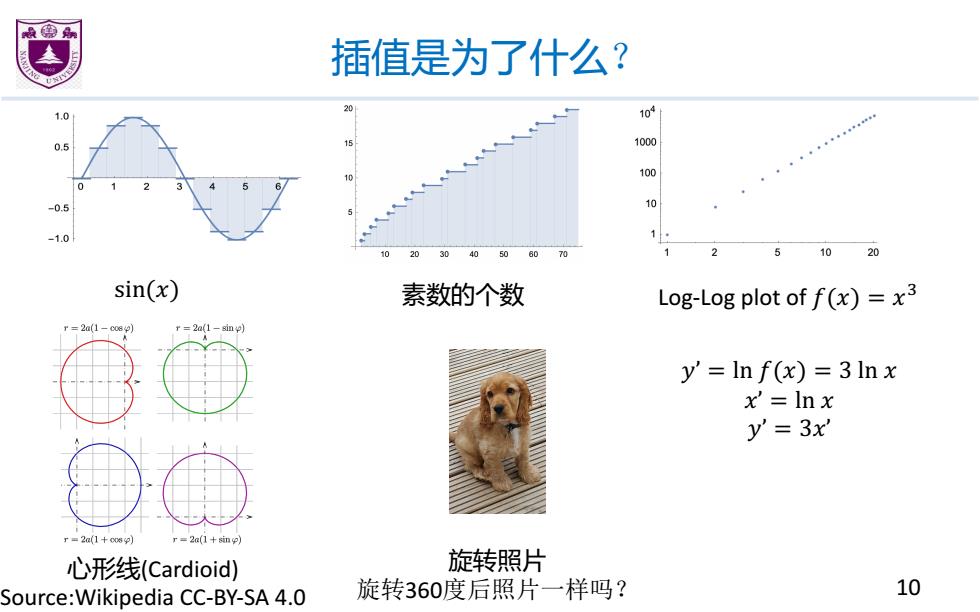
插值是为了什么? 1.0 104 0.5 1000 四 -0.5 10 -1.0 1020 sin(x) 素数的个数 Log-Log plot of f(x)=x3 r=2a(1- =2a(1-in】 y'=In f(x)=3In x x'=Inx y'=3x' r =2a(1 +008p) r=2a(1+np) 心形线(Cardioid) 旋转照片 Source:Wikipedia CC-BY-SA 4.0 旋转360度后照片一样吗? 10
插值是为了什么? 10 sin(�) 素数的个数 Log-Log plot of �(�) = �+ �’ = ln �(�) = 3 ln � �’ = ln � �’ = 3�’ 心形线(Cardioid) Source:Wikipedia CC-BY-SA 4.0 旋转照片 旋转360度后照片一样吗?
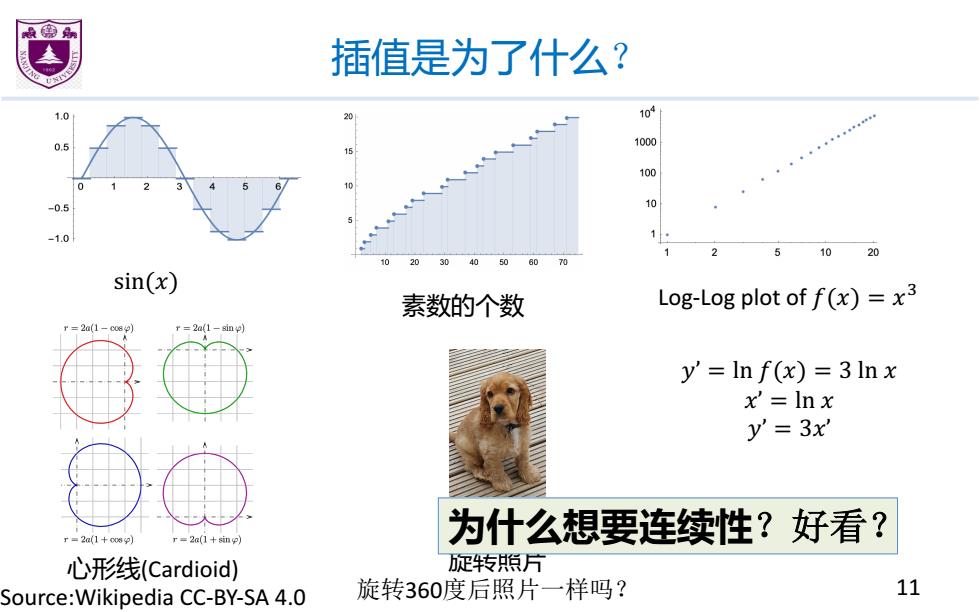
嫩细 插值是为了什么? 1.0 104 0.5 1000 100 0 -0.5 10 -1.0 10 20 60 sin(x) 素数的个数 Log-Log plot of f(x)=x3 =21-c080 y'=In f(x)=3Inx x'=Inx y'=3x r=2(1+008 r=2a(1+i9} 为什么想要连续性?好看? 心形线(Cardioid) 疋转照片 Source:Wikipedia CC-BY-SA 4.0 旋转360度后照片一样吗? 11
插值是为了什么? 11 sin(�) 素数的个数 Log-Log plot of �(�) = �+ �’ = ln �(�) = 3 ln � �’ = ln � �’ = 3�’ 心形线(Cardioid) Source:Wikipedia CC-BY-SA 4.0 旋转照片 旋转360度后照片一样吗? 为什么想要连续性?好看?

插值的连续性 回顾一下不连续函数的数值稳定性: 给定函数f 输入:x+△x 计算:f(x) f(x+△x)-f(x)≈△xf'(x) 在函数不连续性的点上,数值可能非常不稳定! 更进一步的处理,往往需要更高阶的导数 12
插值的连续性 • 回顾一下不连续函数的数值稳定性: • 给定函数� • 输入: � + Δ� • 计算:�(�) � � + Δ� − � � ≈ Δ� �′(�) 更进一步的处理,往往需要更高阶的导数 12 在函数不连续性的点上,数值可能非常不稳定!

用什么插值? 多项式定义: p(x)=ao ax+azx2+a3x3+..+anxn ao,a1,…,an称为多项式的系数 ·若an≠0,则称n为多项式的次数 ·常用表达形式(代数基本定理): p(x)=an(x-r1)(x-r2)...(x-mn) ”一般来说1,r2,…,可能是复数,复数根总是成对出现的 ·为什么使用多项式?如果使用物理电路插值呢?神经网络呢? -回顾Taylor展开,也是多项式 -Taylor展开一般只关注一个点上的近似多项式 -Weierstrass定理:对于连续函数,多项式可以任意地逼近。 13
用什么插值? • 多项式定义: � � = �! + �$� + �*�* + �+�+ + ⋯ + �,�, • �!, �$, … , �,称为多项式的系数 • 若�, ≠ 0, 则称�为多项式的次数 • 常用表达形式(代数基本定理): � � = �, � − �$ � − �* … (� − �,) • 一般来说�$, �*, … , �,可能是复数,复数根总是成对出现的 • 为什么使用多项式?如果使用物理电路插值呢?神经网络呢? – 回顾Taylor展开,也是多项式 – Taylor展开一般只关注一个点上的近似多项式 – Weierstrass 定理: 对于连续函数,多项式可以任意地逼近。 13