河南大学：《电路原理》课程电子教案（课件讲稿）第14章 线性动态电路的复频域分析

3.积分性质 设：Lf(t)]=F(s) 则： 8 F(s) S 例 求：f()=t的象函数 解 由于f()=t=0(5d5

3.积分性质 s F s f t dt t ( ) ( ) 0          则： 设： [ f (t)]  F(s) 例 求: f (t)  t 的象函数 f t t   d t     0 由于 ( ) ( ) f (t) 2 0 1 1 1 ( ) s s s d t              解

4.延迟性质 设：[f(t)川=F(s) 则：[f(t-t)】=eF(s) 证、 当t<t时，f(t-to)=0,令t=t-t 则： f(t-t】=ft. f()edr ef()edr -e sF(S)

4.延迟性质 设： [ f (t)]  F(s) [ ( )] ( ) 0 0 f t t e F s  st 则：   证 , ( ) 0 , 0 0 0 当 t  t 时 f t  t  令  t  t (s) ( ) ( ) [ ( )] ( ) 0 0 0 0 0 ( ) 0 0 0 e F e f e d f e d f t t f t t e dt st st s s t st                            则：

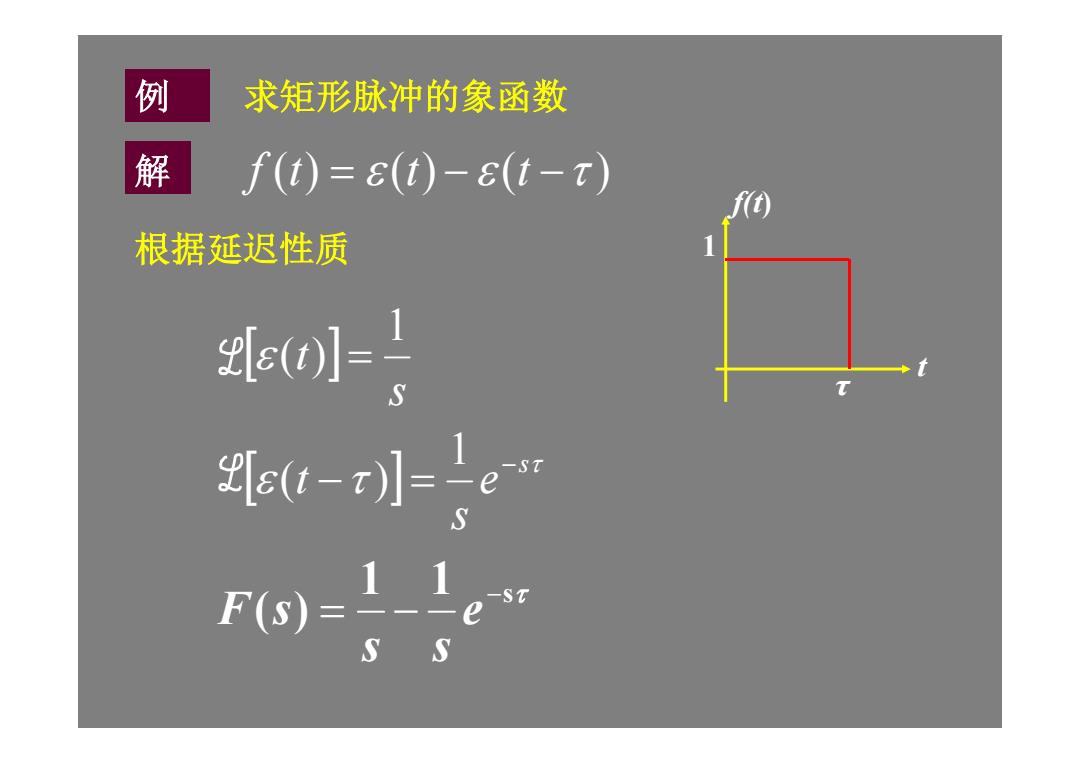
例 求矩形脉冲的象函数 解 f(t)=6(t)-(t-T) 根据延迟性质 (0=1 [e(t-x)】=e F(S)= S

例 1 τ t f(t) f (t)   (t)   (t  ) 1 1 s ( )    e s s F s 求矩形脉冲的象函数 解 根据延迟性质         s e s t s t     1 ( )1 ( )

5.拉氏变换的卷积定理 卷积积分定义 f()*f(0)=f(t-5)f,(5)d5 拉氏变换的卷积定理 若[f(t】=F,(s [f,(t)=F,(s) 则 U0*-5⑤) F (S)F2 (s)

卷积积分定义 f t f t f  f  d t ( )* ( ) (t ) ( ) 2 0 1 2   1  拉氏变换的卷积定理 [ ( )] ( ) [ ( )] ( ) 1 1 2 2 若 f t  F s f t  F s   (s) (s) ( )* ( ) ( ) ( ) 1 2 0 1 2 1 2 F F f t f t f t f t         则   5.拉氏变换的卷积定理

14.3 拉普拉斯反变换的部分分式展开 用拉氏变换求解线性电路的时域响应时，需要 把求得的响应的拉氏变换式反变换为时间函数。 由象函数求原函数的方法： (1)利用公式 f(t)= 上mFse" (2)对简单形式的F(s)可以查拉氏变换表得原函数

14.3 拉普拉斯反变换的部分分式展开 用拉氏变换求解线性电路的时域响应时，需要 把求得的响应的拉氏变换式反变换为时间函数。 由象函数求原函数的方法： (1)利用公式 F s e ds πj f t st c j c j ( ) 2 1 ( )       (2)对简单形式的F(s)可以查拉氏变换表得原函数