
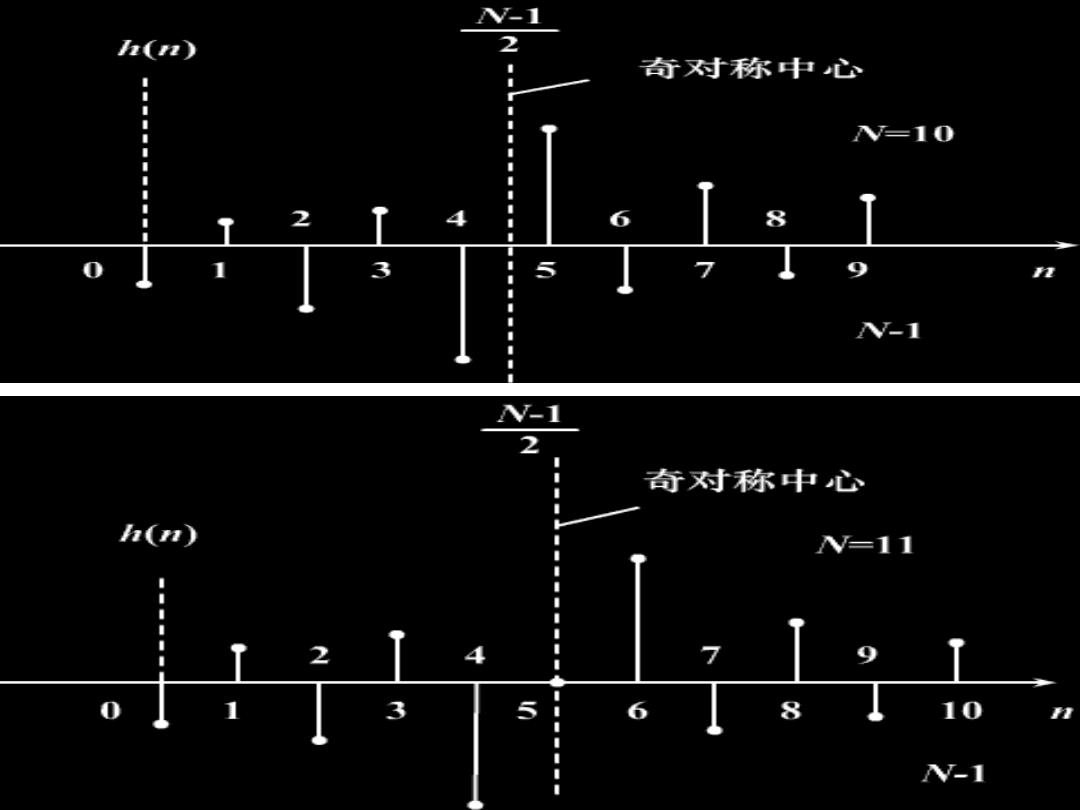
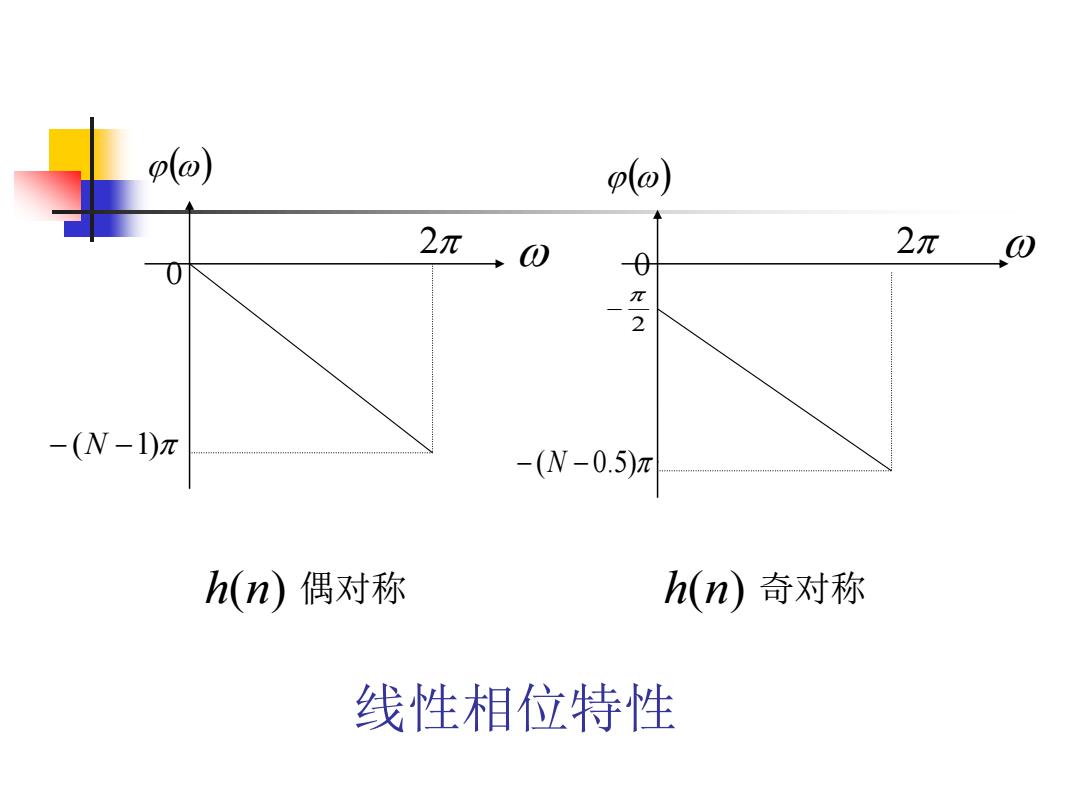
2、第二类线性相位条件证明 若:(o)=B-ao,此时群延时x。=- do(@) 二0 do H(e0)=H(@)ei(B-ao) 类似可以得出 N-1 d- 2 与前一种不同之处 B=± 在于增加乒 的相 2 h(n)=-h(N-1-n) 移 即第二类线性相位(o)=B-ao的充要条件 hn)为奇对称,对称中心为a= W-1 2
2、第二类线性相位条件证明 2 1 ( ) ( ) ( ) ( 1 ) 2 2 N -1 ( ) ( ) ( ) ( ) ( ) − = = − = − − − = = − = − = − N h n a h n h N n H e H e d d j j a g 为奇对称,对称中心为 即第二类线性相位 的充要条件 = = 类似可以得出 若: ,此时群延时 与前一种不同之处 在于增加了 的相 移 2
-1 h(ra) 奇对称中心 =10 8 3 -1 V-1 2 奇对称中心 h(n) V=11 4 1 5 8 10 I V-1
plw) p(o) 2π0 2π 0 ⊙ -(N-1)π -(N-0.5)m h(n)偶对称 h(n)奇对称 线性相位特性
() 2 0 − (N −1) () 2 0 − (N − 0.5) 2 − h(n) 偶对称 h(n) 奇对称 线性相位特性

注意 从第二类线性相位看出: 零频率w=0有2的截距,说明不仅有: W-1 2 个抽样间隔的延时,而且还产生一个90°的相移, 这种使频率皆为90°的网络,称为正交变换网络, 它具有重要的理论和实际意义。 也就是:h(n)为奇对称时,FIR滤波器是一个 具有准确的线性相位的理想正交变换网络
注意 从第二类线性相位看出: 零频率w=0有2的截距,说明不仅有: 也就是:h(n)为奇对称时,FIR滤波器是一个 具有准确的线性相位的理想正交变换网络。 个抽样间隔的延时,而且还产生一个90的相移, 这种使频率皆为90的网络,称为正交变换网络, 它具有重要的理论和实际意义。 2 −1 = N

4.1.2幅度特性 由于hn)的长度N取奇数还是偶数,对H(w)的特 性有影响,因此,对于两类线性相位,下面 我们分四种情况讨论其幅度特性的特点: (1)h(n)=hN-1-n),即h(n)为偶对称,N=奇数 (2)h(n)=hN-1-n),即h(n)为偶对称,N=偶数 (3)h(n)=-hN-1-n),即h(n)为奇对称,N=奇数 (4)h(n)=-hN-1-n),即h(n)为奇对称,N=偶数
4.1.2 幅度特性 由于h(n)的长度N取奇数还是偶数,对H(w)的特 性有影响,因此,对于两类线性相位,下面 我们分四种情况讨论其幅度特性的特点: (1)h(n)=h(N-1-n),即h(n)为偶对称,N=奇数 (2)h(n)=h(N-1-n),即h(n)为偶对称,N=偶数 (3)h(n)=-h(N-1-n),即h(n)为奇对称,N=奇数 (4)h(n)=-h(N-1-n),即h(n)为奇对称,N=偶数