广东海洋大学：《数字信号处理 Digital Signal Processing》课程教学资源（PPT课件讲稿）第四章 有限长单位脉冲响应（FIR）滤波器的设计方法

1 2 3 4 5 n 1 2 34 5 6 n (a) (b) n) h(n) 1 2 2 3 (c) (d)

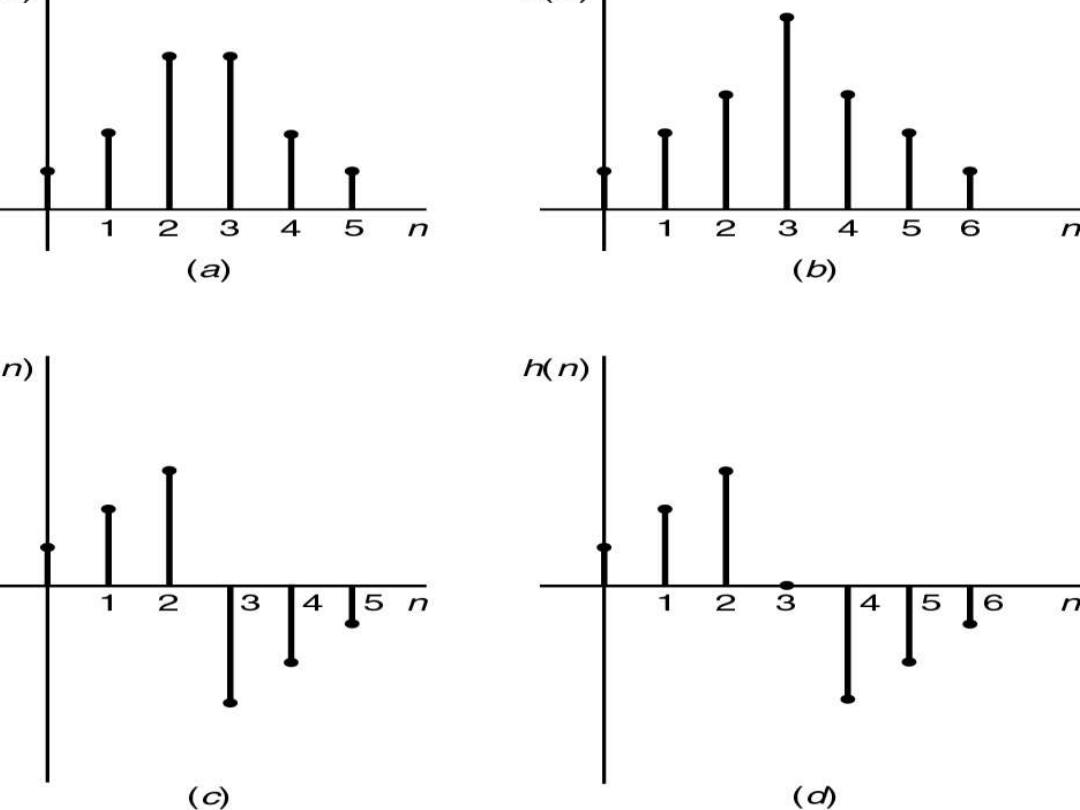
1、第一种情况： h(n)=h(N-1-n)偶对称，N=奇数 He）=Hoeo =∑yhan)em n=0 N-11 oo n=0 W+] n= 2 N-3 -2啡+-9 n=0

1、第一种情况： h(n)=h(N-1-n)偶对称，N=奇数 ( ) ( ) ( ) ( ) ( ) ( ) ( )         − − − = − − − − − + = −       − − − − = − − = −       − = + +  +      − = + = =     2 1 2 3 0 1 1 2 1 2 1 1 2 1 0 1 0 2 1 2 1 ( ) N j N n j n j N n N N n j n N j N n j n N n j n j j e N h n e e h e h n e N h n e h h n e H e H e           

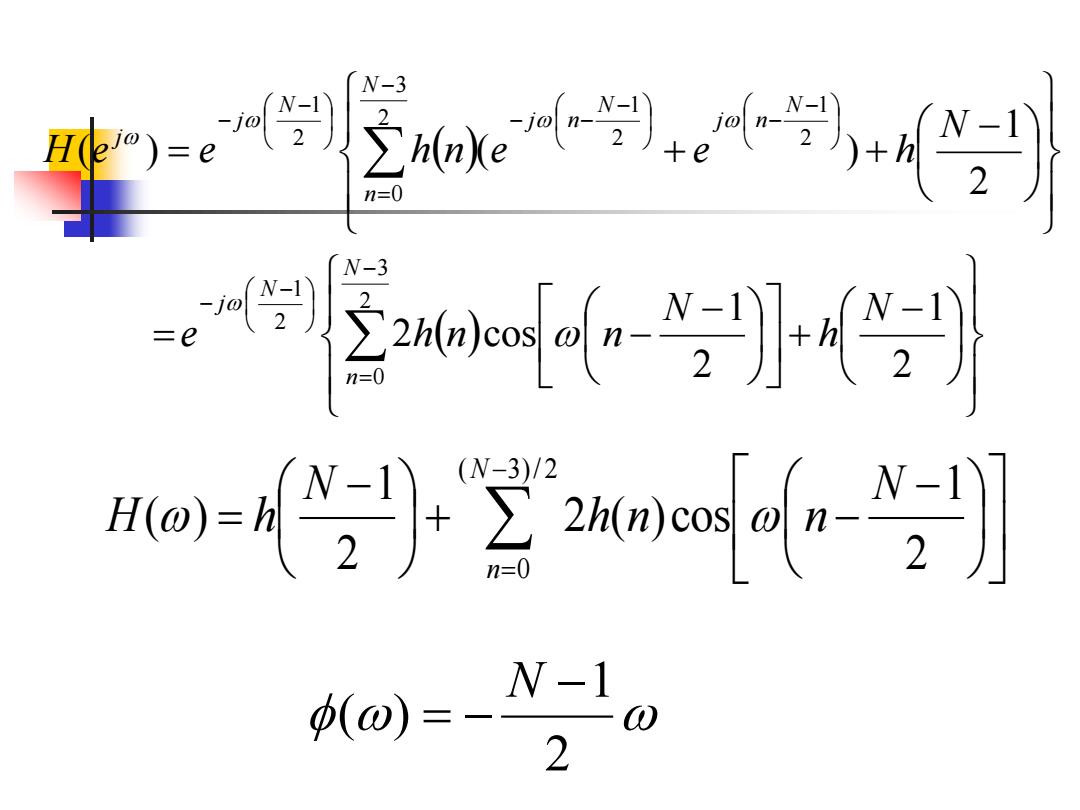
欢学5w N-3 n=0 州 W-3 i=室woo- (N-3)/2 n=0 (o)=- W-1 2

( ) ( )                 − +            − = −                 − = + +   − =       − −       − − − =       −  − −      − − 2 1 2 1 2 cos 2 1 ( ) ( ) 2 3 0 2 1 2 1 2 3 0 2 1 2 1 N h N e h n n N H e e h n e e h N n N j N j n N n N j n N j j        − =             −  + −      − = ( 3)/ 2 0 2 1 2 ( ) cos 2 1 ( ) N n N h n n N H  h     2 1 ( ) − = − N

W-1 令m=n 2 4o)=2 (N-1)/2 + 2m)cosom a0=2m=24v2n 整理后得： N-1 H(@)=>a(n)cosno n=0 看出：cos(nw)对于w=O,π，2π皆为偶对称，所以幅度 函数H(w)也对w=O,元，2π皆为偶对称。且H(0)、H(π/2)， H(π)，H(2元)都可不为零。（只要h(N-1)/2)不为零。所以w 从0-→2π范围内，无任何约束，可以设计成任何一种滤 波器。低通、高通、带通、带阻)

( )   − = − = =       + −  =      − = + −  +      − = − = − 2 1 0 ( 1)/ 2 1 ( ) cos 2 1 , ( ) 2 2 1 (0) ) cos 2 1 2 ( 2 1 ( ) 2 1 N n N m H a n n n N a n h N a h m m N h N H h N m n     整理后得： 令 令 看出：cos(nw)对于w=0,,2皆为偶对称，所以幅度 函数H(w)也对 w=0,,2皆为偶对称。且H(0)、H(/2), H(),H(2)都可不为零。(只要h ((N-1)/2)不为零。所以w 从0→ 2范围内，无任何约束，可以设计成任何一种滤 波器。低通、高通、带通、带阻）

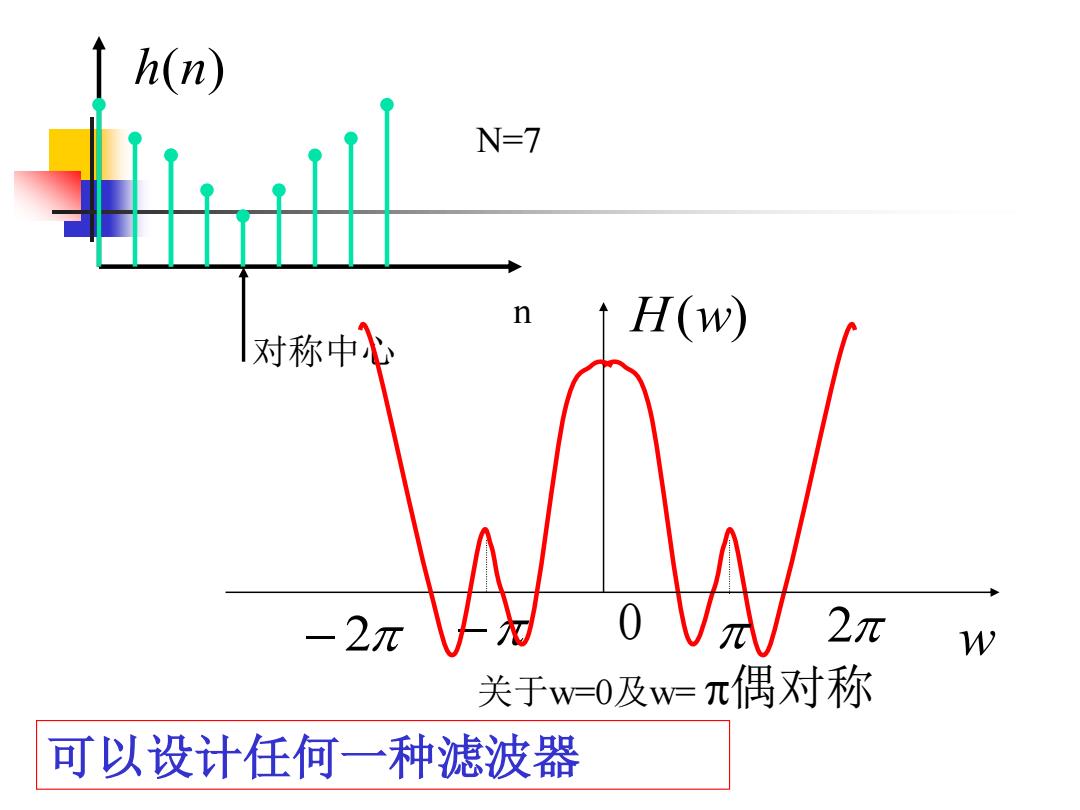
h(n) N=7 对称中 ↑H(w) -2元 2元 W 关于w=0及w=π偶对称 可以设计任何一种滤波器

n 对称中心 N=7 H(w) − 2 − 0  2 w 关于w=0及w= 偶对称 h(n) 可以设计任何一种滤波器