
∑h(nsin[a-njo]=0 n=0 按付氏级数的性质,若有解,此解必为唯一 利用数字归纳法可证得 W-1 Q= 2 h(n)=h(N-1-n) ,0≤n≤N-1 即第一类线性相位的充要条件: I)h(n)为偶对称,其对称中心在a= N一1处 2 2)群时延x=0= 、(为(n阶数的一半
( ) ( ) ( ) ( ) ( ( ) ) 2 N -1 2) 2 1 1) ( ) : 1 ,0 1 2 1 sin 0 1 0 群时延 为 阶数的一半 为偶对称,其对称中心在 处 即第一类线性相位的充要条件 利用数字归纳法可证得 按付氏级数的性质,若有解,此解必为唯一 h n N h n h n h N n n N N h n n N n = = − = = − − − − = − = − =
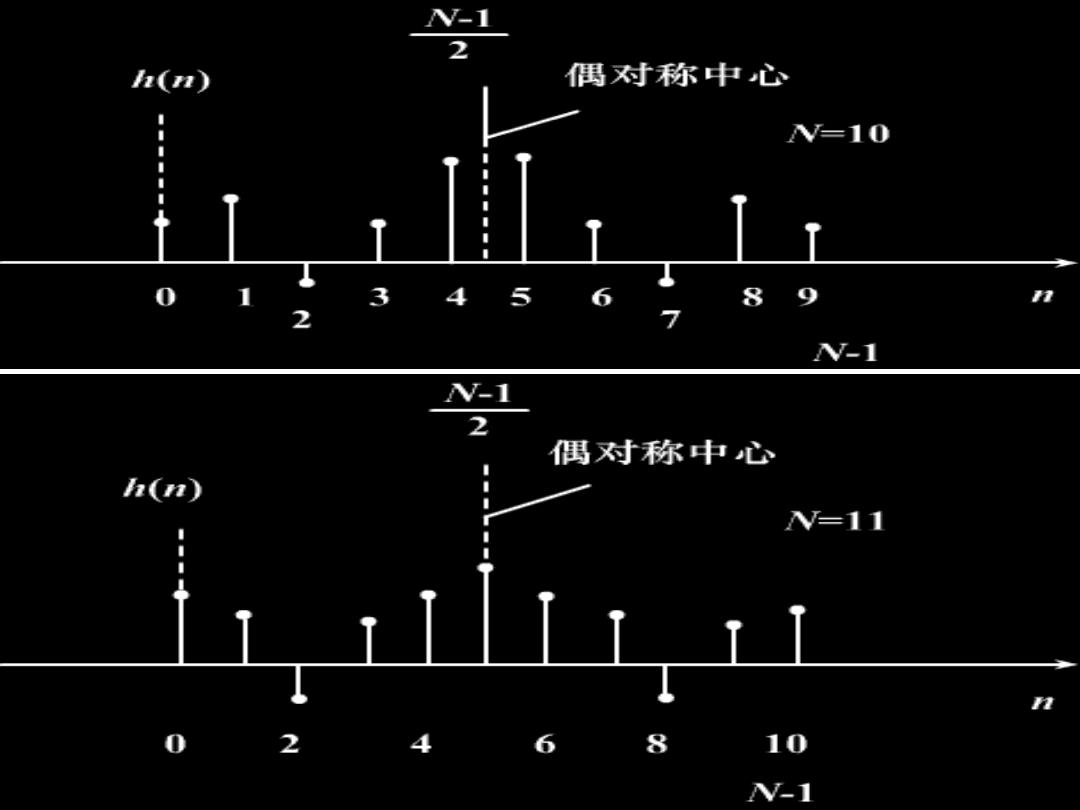
V-1 2 a(n) 偶对称中心 =10 8 17 V-1 V-1 2 偶对称中心 h(n =11 0 4 6 8 10 V-1

另外,证明方法 1)第一类线性相位线性相位条件证明 h()为偶对称,该滤波器具有第一类线性相位特性 即h(n)=h(N-1-n): He)=m-E"-空MN-1-m= n三0 令W-1-n=m H(e)=∑m)m=-Nw= N- .H(-)=>h(m)=m..H()==-N-DH(=-) m=0
1)第一类线性相位线性相位条件证明 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( 1 ) ( ) ( 1 ): ( ) ( 1) 1 1 0 1 1 0 ( 1) 1 0 ( 1 1 0 1 0 − − − − = − − = − − − = − − − − = − − = − = = = = − − = = = − − = − − H z h m z H z z H z H z h m z z h m z N n m H z h n z h N n z h n h N n h n N N m m N m N m N m N m N n n N n n ) 令 即 为偶对称,该滤波器具有第一类线性相位特性 另外,证明方法

则可将H(z)表示为: (2)=[H(2)+zw-H(z1刀 N-I 1-2 mz-0+2-2(n)z" n=0 n=0 1 2 ∑m)2"+zw-z“] n=0 W-1 (N-1) N-1 -n+ N 2 2 三 Z 2 ∑h(n) Z 十Z n=0 2 将z=e"代入上式,得到:
将 代入上式,得到: 则可将 表示为 j w N n N n N n N N n n N n N n N n N n n N z e z z z h n h n z z z h n z z h n z H z H z z H z H z = + = = + = + = + − = − − − − + − − − = − − − − = − − − = − − − − 1 0 2 ( 1) 2 1 2 1 1 0 ( 1) 1 0 ( 1) 1 0 ( 1) 1 2 ( ) ( ) 2 1 ( ) ( ) 2 1 [ ( ) ( )] 2 1 ( ) ( ) :
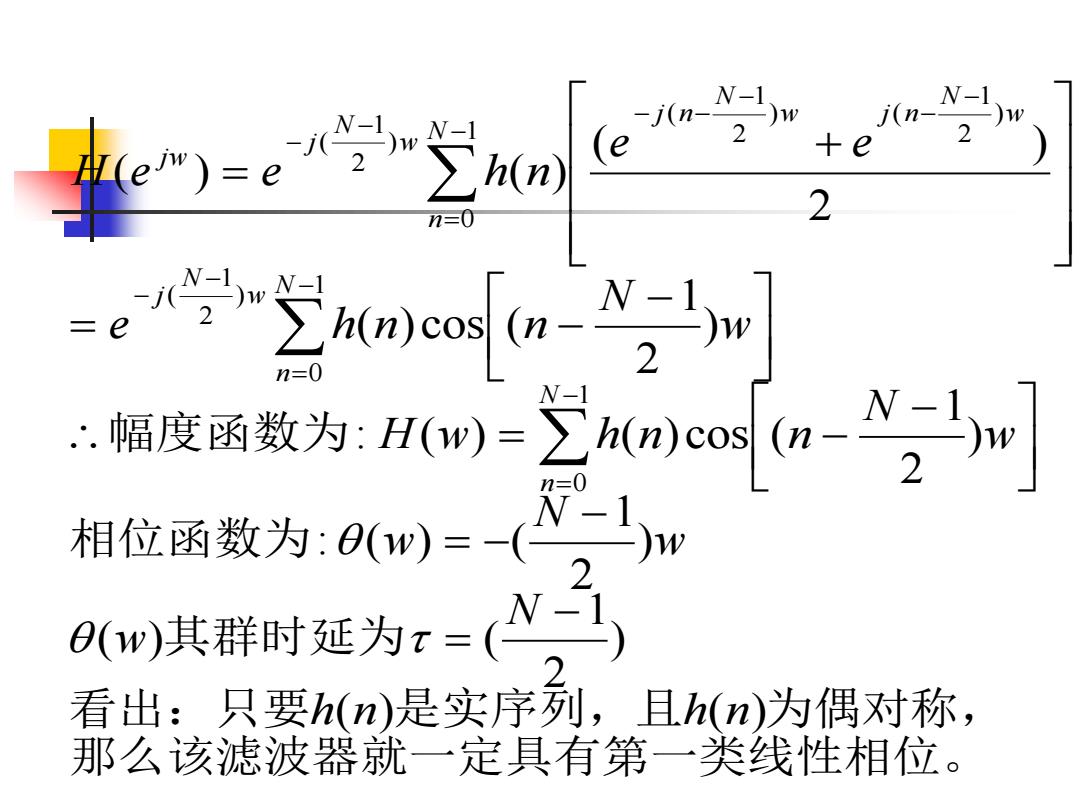
j(n- N-)w N-1 e)=em j(n- (e +e 2 n0 2 noth n=0 他度商效为m三u小anNw N- 相位函数为:)=-(w n=0 时延为:=心弓 看出:只要h(n)是实序列,且h(n)为偶对称, 那么该滤波器就一定具有第一类线性相位
那么该滤波器就一定具有第一类线性相位。 看出:只要 是实序列,且 为偶对称, 其群时延为 相位函数为 幅度函数为 ( ) ( ) ) 2 1 ( ) ( ) 2 1 : ( ) ( ) 2 1 : ( ) ( ) cos ( ) 2 1 ( ) cos ( 2 ( ) ( ) ( ) 1 0 1 0 ) 2 1 ( 1 0 ) 2 1 ) ( 2 1 ( ) 2 1 ( h n h n N w w N w w N H w h n n w N e h n n e e H e e h n N n N n w N j N n w N w j n N j n w N j j w − = − = − − = − − = − + = − = − = − − − = − − − − − − −