
补充定义 1、时延:所谓时延是指信号通过传输通 道所需要的传输时间。 ■2、群时延 它是滤波器平均延迟的一个度量,定义为 相频特性对角频率w的一导数的负值。即: t(o)=- d(arg H(e)) do(w) dw do 当(o)=常数时,DF具有线性相位, 即相频特性argH(eo)是o的线性函数
补充定义 ◼ 1、时延:所谓时延是指信号通过传输通 道所需要的传输时间。 ◼ 2、群时延: 它是滤波器平均延迟的一个度量,定义为 相频特性对角频率w的一阶导数的负值。即: 即相频特性 是 的线性函数。 当 常数时, 具有线性相位, arg ( ) ( ) (arg ( )) ( ) ( ) j j H e DF d d d d H e = = − = −

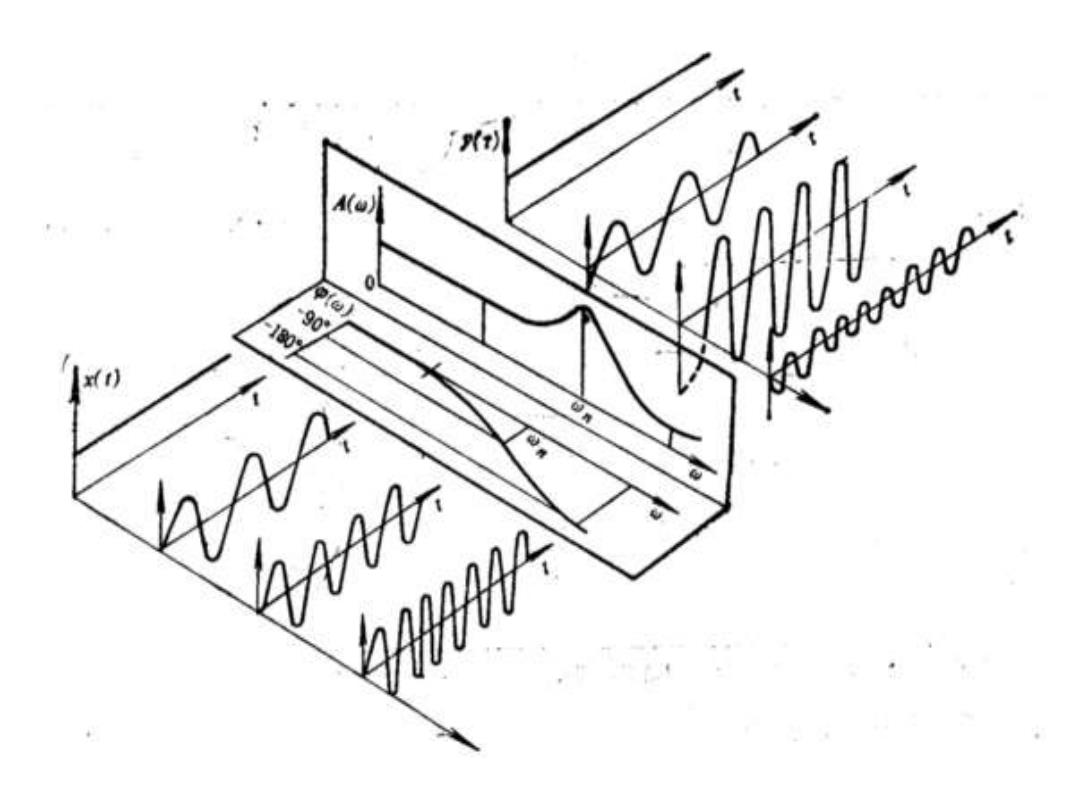
幅频特性和相频特性 输出信号与输入信号的幅值比是的非线性函数,称其 为系统的幅频特性,记为A(⊙).它描述了在稳态 情况下,当系统输入不同频率的谐波信号时,反映 幅值比随频率而变化的规律,其幅值的衰减(A<1) 或增大(A>1)特性. 输出信号与输入信号的相位差(或称相移)也是的非 线性函数,称为系统的相频特性.它描述了在稳态 情况下,当系统输入不同频率的谐波信号时,反映 相位差随频率而变化的规律,其相位产生超前[Φ (o)>0]或滞后[Φ(w)<0]的特性.对于物理 系统,相位一般是滞后的,即一般是负值
幅频特性和相频特性 输出信号与输入信号的幅值比是的非线性函数,称其 为系统的幅频特性,记为A(ω).它描述了在稳态 情况下,当系统输入不同频率的谐波信号时,反映 幅值比随频率而变化的规律,其幅值的衰减(A<1) 或增大(A>1)特性. 输出信号与输入信号的相位差(或称相移)也是的非 线性函数,称为系统的相频特性.它描述了在稳态 情况下,当系统输入不同频率的谐波信号时,反映 相位差随频率而变化的规律,其相位产生超前 [Φ ( ω )> 0]或滞后[Φ( ω ) <0]的特性.对于物理 系统,相位一般是滞后的,即一般是负值
A(u小 名 0 ARA7 0

2、FIR滤波器具有线性相位的条件 第一类线性相位条件证明 若:中(0) =-C0, Ale)=H(o)e=Hobe=分hri)e n=0 →IH(o)cos(oa)-jHo)sin(oa)=∑hln)cos(nm)-∑hn)sin H(@)cos(oa)=>h(n)cos(no) n=0 W- H(o)sin(oa)=∑n)sin(no) n=0
2、FIR滤波器具有线性相位的条件 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − = − = = = − = − = − = − = − = − − 1 0 1 0 1 0 1 0 1 0 ( ) sin( ) sin( ) cos( ) cos( ) cos( ) sin( ) cos( ) sin( ) - N n N n N n N n N n j j j j n H h n n H h n n H j H h n n j h n n H e H e H e h n e 若: ( )= , 第一类线性相位条件证明

式中H(o)是正或负的实函数。等式中间和等 式右边的实部与虚部应当各自相等,同样实部 虚部的比值应当相等 sin(ao) )sin(on) n=0 cos(a0) ∑hn)cos(on) n=0 →∑hn)cos(onm)sin(ao)=∑h(n)sin(om)cos(ao) n=0 W-] →∑h(n)sn[a-nlo]=0 n=
式中 H(ω)是正或负的实函数。等式中间和等 式右边的实部与虚部应当各自相等,同样实部 与虚部的比值应当相等: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )sin ( ) 0 cos sin sin cos cos sin cos sin 1 0 1 0 1 0 1 0 1 0 − = = = − = − = − = − = − = N n N n N n N n N n h n n h n n h n n h n n h n n