
c-Bi y-景一2E7Reos8r…是(1-6eBe).(14到 对于如图7b所示的固定端的情形,反力R及弯矩M,的大小 可由支点的挠度及斜率为幂这两个条件求得.考虑到离支点很远 之处挠度等于g/原并运用式(11)和(12),得下列两个用以計算R 及M的方程式”: -g三 1 -(R+BMo) 28EI 和 1 0= (R+28Mo) 28EI 从而得 M-一88景R=48E1景-骨 (15) M的負号表明弯矩的方问如图7b中左面的箭头所示 习 1.武求一弹性基硒上牛无限长梁的挠度曲藏,梁的一端餃支, 而其:上作用着一力偶Mo,图8. 解将8=0代入式(11),得鉸支点的反力为 P=BMa. 将此P值代入式(11),得 ya Me:sin Bx= 28 EI: 28225(Bx) (16) 好8 图9 遂次微分之,得 )在式(11)P(2)中代天=一R,因为反力的正是取为向上的 r13

y=284,中(Bx), dx 无 M=一E1 =M·(Bx), dx2 (6) V=一EI y=-BM·p(Bx. 2.武求作用于…弹性基础上的半无限长梁一端的弯矩M,及 力P,图9,如果該端的挠度8和斜率α为已知. 解.将已知的8和(dy/x)=a代入式(11)和(12),得 M和P. 3.試求一弹性基础上的牛无限长梁由截荷P产生的挠度曲 籁,P的作用点离梁自由端A的距离为c,图10. 解。股梁延伸到A端的左边,如壶後所示。对于这一情形, 式(3)給出x>0时的挠度曲後,根 据式(7)井运用对称条件,在假想的 无限长梁的截面A处得: M= 48 (c) V= 卫0Bc). 为了求得A端自由的牛无限长梁所 图 10 需的挠度曲殺,显然須将牛无限长 梁由图10b所示的力产生的挠度与假想无限长梁的挠度相迭加. 这样,运用式(3),(11)及(c),当x>0时,得 y=器p(a)+29p9[:+。1+ +BMO[B()]-BMC[B(+c)]} 2是p(B:)+毁{8Bc0IB(E+e]+ =P +(Be)0[B(x+e1- 。14

(Bc)[B(x+c)]. (d) 2 此式也可用于一c<<0;这时只須以的絕对值代替(B:)中 的x卸可. §3.弹性基础上有限长的梁.弹性基础上有限长梁的弯曲 也可用无限长梁的解[式(3)]及迭加法来究,为了說明此方 法,我們来研究两喘自由的有眼长梁受两个对称作用力P的情形, 图11a.这与枕木受鋼軌压力作用的情形相以.§1的通解式(b) 可应用于梁的这三个部分,而积分常数可由两端点及載荷作用点 的条件定出.然而,如将图11b和11c所示的无限长梁的两种受裁 特形之解迭加,就可更容易 地求得所需之解。在图11b 上有两个力P作用于一无限 长的梁上.在图11c上无限 长的梁承受力Q,及弯矩M, Q0及M,均作用于梁的AB 部分之外,件无眼地接近于 点A及点B,点A及点B相 当于骸梁的两个自由瑞,图 11,不难看出,知适当地选 择力Q。及弯矩M,就可使 无限长梁(如图11b所示)的 藏面A及B处由两个力P 图1 生的弯矩及剪力等于零.于是无限长梁的中周部分显然与图11 所示的有限长梁的情形相同,而对有限长梁弯曲的所有需要的数 据可由图11b及11c所示的两种情形的迭加而求得 为了列出用以确定适当的M及Q,值的方程式,我們来研究 l)这-一分析方法是由M.Hctenyi所袅腰由米的,Final Repori,2 d Congr. Internat,Assoc,Bridge and Stritetural Engng,Berlin,I938.井参看做的 “Beams on Elastic Foundation”,P.38. ■15◆
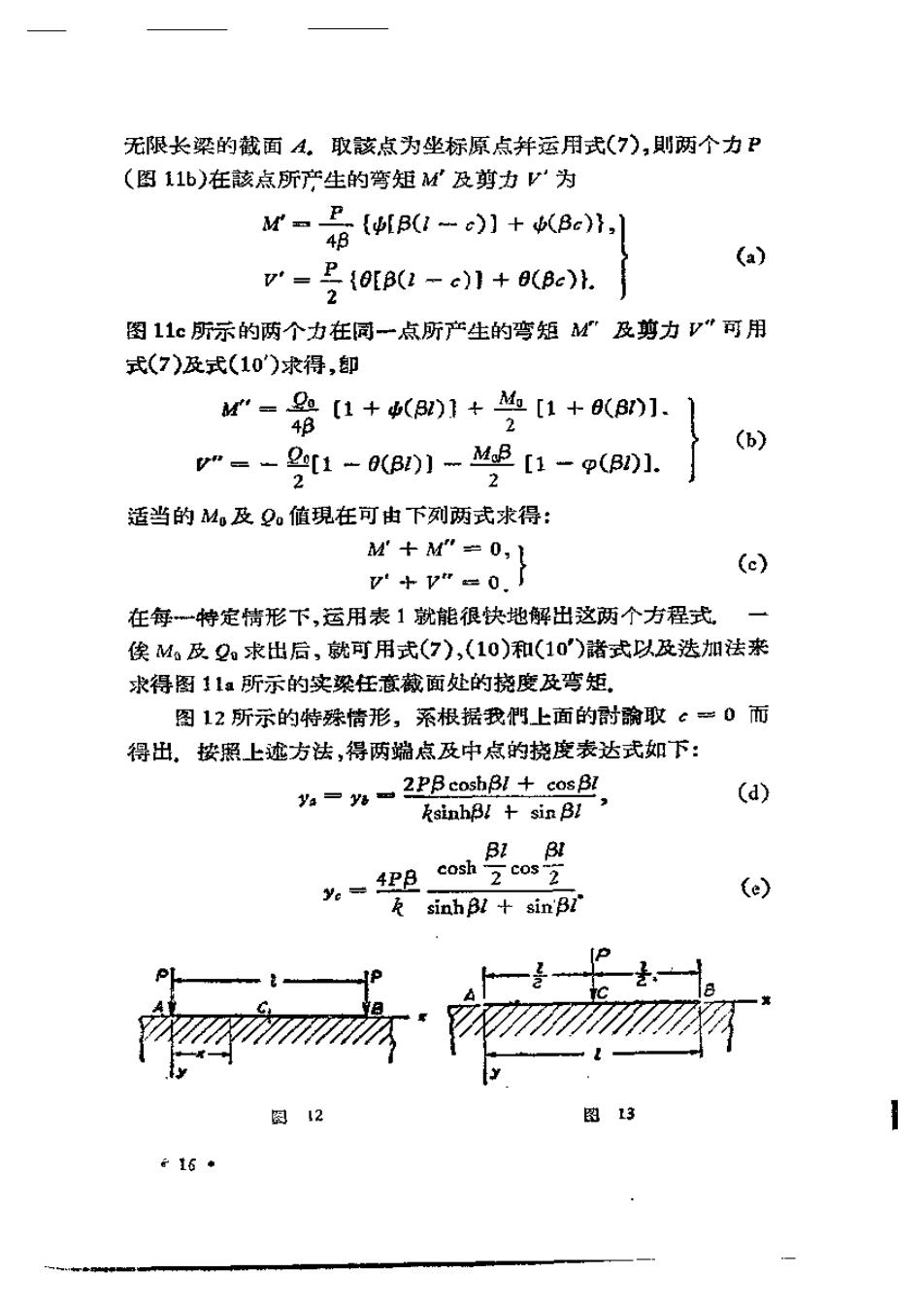
无限长梁的截面A。取骸点为坐标原点并运用式(7),則两个力P (图11b)在該点所产生的筲矩M及剪力V'为 r-B{B(1-c】+(Bc),l 48 (a) = (0[B(2-c)1+0(Bc)1. 3 图11c所示的两个力在同一点所产生的弯知M”及剪力V”可用 式(7)及式(10)求得,卸 M”-81+a)1+丝[1+9(801. 48 (b) V”=一 2[1-9(B21-4,3[1-p(B01. 适当的M,及9值現在可由下列两式求得: M+M”=0, v+"=0. (c) 在每…特定情形下,运用表1就能很快地解出这两个方程式. 俟M及2求出后,就可用式(7),(10)和(10)諾式以及法加法来 求得图11a所示的实梁任意藏面处的挠度及弯矩 图12所示的特殊情形,系根据我們上面的时前取c=0而 得出,按照上远方法,得两端点及中点的挠度表达式如下: 为-%=2 PB cosh31+cosB2 (d) ksinhB!+sin B! BZ BI .=4P3 cosh 2cc0s号 (e) k sinhBl+sin'B!" 12 13 16*

中点的弯矩为 BI B Me=一 2p sinh 2 sin 2 (f) B sinhBl+sin Bl 有一单个酸荷作用于中点的楷形图13)也可按上画图11a所 示的情形求得,只須取c1/2并以P代2P即可,这样,我們 求得两端点及中点的挠度表达式为: 8L BZ a=y%= 2P8 、 cosh'2 cos"2 sinhBI sin Bi' (g) y.=P2cosh8÷c0sBl+2 (h) 2原 sinhB!sin Bl 我們求得截荷下的弯矩为 M。=P coshBL-cos8L (i) 4 3 sinhBl÷sinB1 用于图11a所示的对称情形的方法也可用于图14a所示的反 对称情形。这时Q及Mo也 可表示一反对称载荷組,如 图14c所示.确定适当的Q。 及M。值时、可很快写出与 (a),(b)和(c)諸式类似的方 程粗,一俟P。及M箅山 后,对图14a所示梁弯曲的 所有需要的数据就可由图 14b和14c所示两种桔形的 迭加而求得 (e 有了梁受对称载荷及反 对称载荷时的解,我們就利 图14 用迭加原理很快求得受任意載荷时的醉.例如、图15a所示的不 对称情形的解系由图15b和15心所示的对称和反对称情形的解的 迭加矿求得。图6所示的間題用同样方法处理,对于每一种 。7