
dy=2BCe-B:(sin Bx-cosBx) (e) dx2 diy-48Ce-Bs cosBx. (f) dx3 現在常数C可由右边这段梁在x=0处的剪力等于一(P/2)(图 1b)这一事实来确定.負号系按照我們对剪力符号的約定而定的 (参看原书上卷第75一76頁).于是 (V)= M 或用式(),得 E1x·483C= 从而得 C= P 8BET 将此值代入式(d)和(e),得下列的挠度及弯矩曲线方程式: P y= -COs Bx+sin Bx)=PB(COsBx+sin Bx),(3) 8B EI. 2k M=一E,=-er(nB-)。 (4) dx2 4β 作图时,式(3)和式(4)各为一振幅渐减的波状曲棱 这些曲镜的 波长4河用函数cosBx和sinBx的周期表示,即 2=2r1 4EI: (5) 为使挠度、弯矩及剪力的計算簡化起鬼,刻出数字表(表1),表 中所用的符号如下: p=e Br(cosBx sin Bx); =-e-x(sinBx-cosBx); (6) 6=e-Bx cos Bx;6=e-8 sin Bx. 图2表示图数P及中的图羲
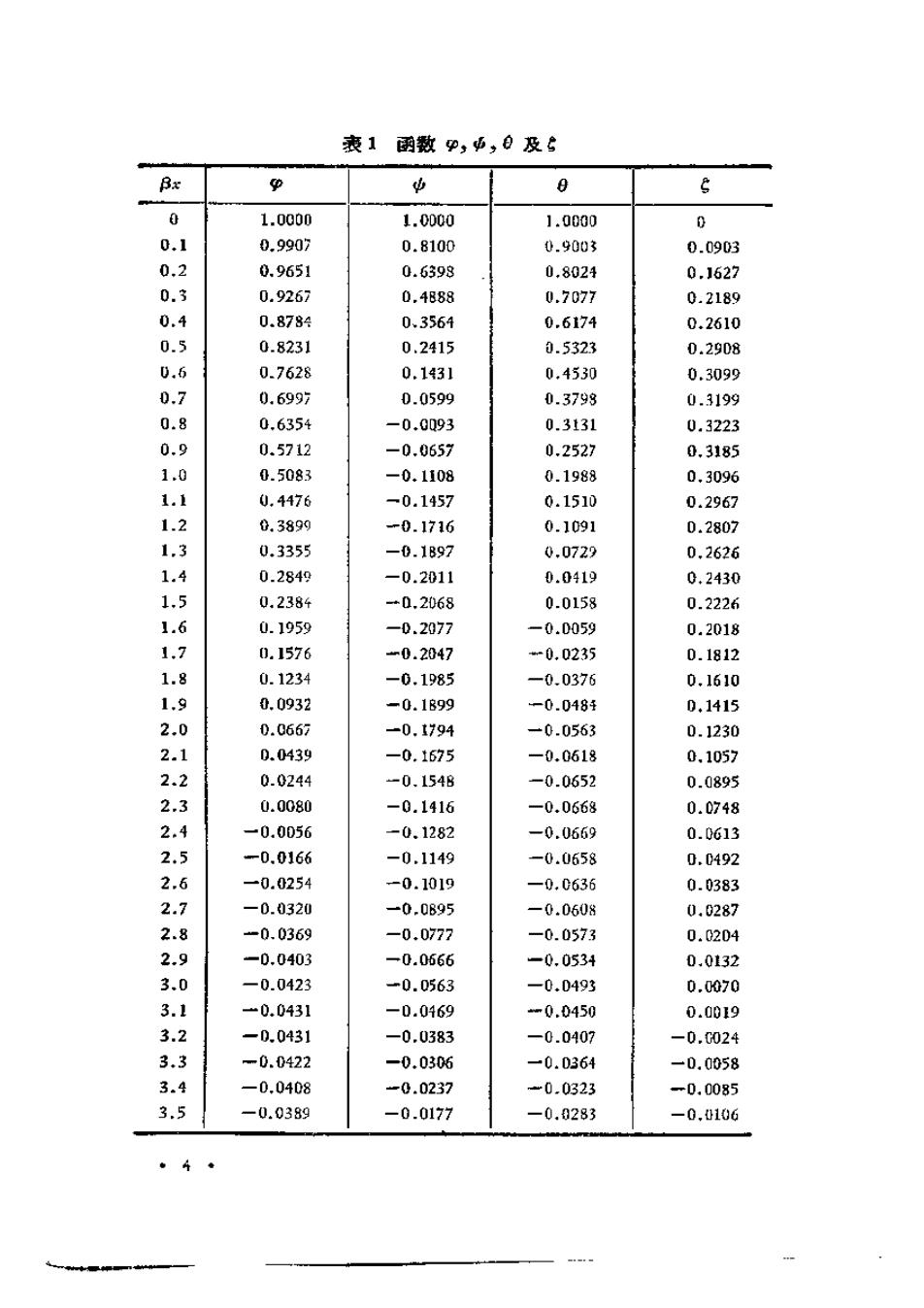
表1函数p,5,日及6 Bx 中 中 0 0 1.0000 1.0000 1.0000 0 0.1 0.9907 0.8100 0.9003 0.0903 0.2 0.9651 0.6398 0.8021 0.1627 0.3 0.9267 0.4888 0.7077 0.2189 0.4 0.8784 0.3564 0.6174 0.2610 0.5 0.8231 0.2415 1.5323 0.2908 0.6 0.7628 0.1931 0.4530 0.3099 0.7 0.6997 0.0599 0.3793 0.3199 0.8 0.6354 -0.0093 0.3131 0.3223 0.9 0.5712 -0.0657 0.2527 0.3185 1.0 0.5083 -0.1108 0.1988 0.3096 1.1 0.4476 -0.1457 0.1510 0.2967 1.2 0.3899 -0.1716 0.1091 0.2807 1.3 0.3355 -0.1897 0.0729 0,2626 1.4 0.2849 -0.2011 0.0419 0.2430 1.5 0.2384 +0.2068 0.0158 0.2226 1.6 0.1959 -0.2077 -0.0059 0.2018 1.7 0.1576 -0.2047 -0.0235 0.1812 1.8 0.1234 -0.1985 一0.0376 0.1610 1.9 0.0932 -0.1899 -0.048 0.1415 2.0 D.0667 -0.1794 -0.0563 0.1230 2.1 0.0439 -0.1675 -0.0618 0.1057 2.2 0.0244 -0.1548 -0.0652 0.0895 2.3 0.0080 -0.1416 -0.0668 0.0748 2.4 一0.0056 -0.1282 -0.0669 0.0613 2.5 -0.0166 -0.1149 -0.0658 0.0492 2.6 一0.0254 -0.1019 一0.0636 0.0383 2.7 一0.0320 →0.0895 -0.0608 0.0287 2.8 -0.0369 -0.0777 -0.0573 0.0204 2.9 -0.0403 一0.0666 -0.0534 0.0132 3.0 -0.0423 -0.0563 -0.0493 0.0070 3.1 -0.0431 -0.01469 -0.0450 0.0019 3.2 -0.0431 一0.0383 -0.0407 -0.0024 3.3 -0.0422 -0.0306 一0.0364 一0.0058 3.4 一0.0408 -0.0237 -0.0323 -0.0085 3.5 -0.0389 -0.0177 一0.0283 -0,0106

镀表1 Bx p 中 6 6 3.6 -0.0366 -0.0124 -0.0245 -0.0121 3.7 -0.0341 -0,007y -0.0210 -0.0131 3.8 -0.0314 -0.000 -0.0177 -0.0137 3.9 -0.0286 一0.0008 -0.0147 一0.0140 4.0 -0.0258 0.0019 -0.0120 -0.0139 4.1 -0.0231 0.0040 -0.0095 一0.0136 4.2 -0.0204 0.0057 -0.0074 -0.0131 4.3 -0.0179 0.0070 -0.0054 -0.0125 4.4 -0.0155 0.0079 -0.0038 -0.0117 4.5 -0.0132 0.0085 -0.0023 -0.0108 4.6 -0.0111 D.0089 -0.0011 -0.0100 4.7 一0.0092 0.009t 0.000k -0.0091 4.8 -0.0075 0.0089 0.0007 -0.0082 4.9 -0.0059 0.0087 0.0014 -0.0073 5.0 -0.0046 0.0084 0.0019 -0.0065 5.1 一0.0033 0.0080 0.0023 一0.0057 5.2 -0.0023 0.0075 0.0326 一0.0U49 5.3 -0.0014 0.0069 0.0028 -0.0042 5.4 -0.0006 0.0064 0.0029 -0.0035 5.5 0.0000 0.0058 0.0029 一0.0029 5.6 0.0005 0.0052 0.0029 …0.0023 5.7 0.0010 0.0046 0.0028 -0.0018 5.8 0.0013 0.0041 0.0027 一0.0019 5.9 0.0015 0.0036 0.0026 一0.0010 6.0 0.0017 0.0031 0.0024 -0.0007 6.1 0.0018 0.0026 0.022 -0.0004 6.2 0.0019 0.0022 0.0020 一0.0002 6.3 0.0019 0.0018 0.0018 +0.0001 6.4 0.0018 0.0015 0.0017 0.0003 6.5 0.0018 0.0012 0.0015 0.0004 6.6 0.0017 0.0009 0.0813 0.0005 6.7 0.0016 0.0006 0.0011 0.0006 6.8 0.0015 0.0004 0.0010 0.0006 6.9 0.0014 0.0002 0.c008 0.0006 7.0 0,0013 0.0001 0.0007 0.0006 5
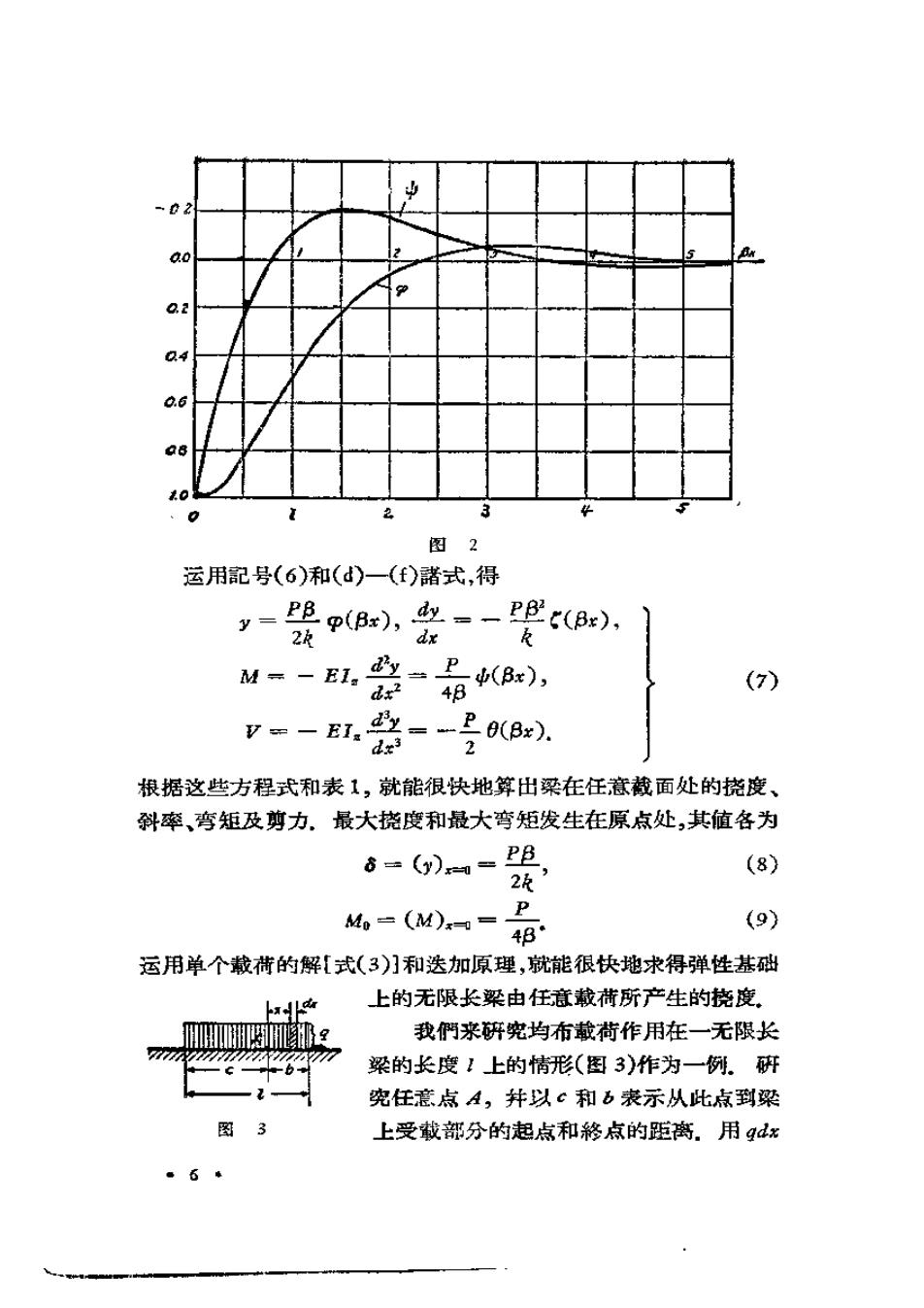
-2 ao 2 a.2 0.6 as 1.0 图2 运用配号(6)和(d)一(f)諾式,得 (Bs),(B). 2k M--E1,坠=(Bx), dx2 48 (7) =一 E1,=-29(8x). dx3 2 根据这些方程式和表1,就能很快地算出梁在任意截面处的挠度、 斜率、弯矩及剪力。最大挠度和最大弯矩发生在原点处,其值各为 6=(y)= PB (8) 2k M。=(M)x0= P 48 (9) 运用单个裁荷的解[式(3)]和迭加原理,就能很快地求得弹性基础 上的无限长梁由任意裁荷所产生的挠度, 补ε 我們来研究均布載载荷作用在一无限长 n77W7 - 梁的长度1上的情形(图3)作为一例。研 究任意点A,并以(和b表示从比点到梁 图3 上受截部分的起点和愁点的距离.用gdx 。6

代替式(3)中的P,得载荷元gdx在A点所产生的挠度为 qdxe(cosBx sin B:). 88EI 于是,分布在长度,上的戟荷在A点所产生的挠度为 2-68 gdx eB(Cos Bx sin Bx)+ 88 EI. 儿.(oB版+血B) 4(2-e-动cosb=。-cos Bc). (g) 2克 如果c和b均很大,则e和e-e之值将很小,从而挠度[式(g)] 将近以等于q/;郎在离杆上受載部分两端很远的各点,杆的弯曲 可忽略不計,并可假設均布截荷g被值接传至弹性基硒上,当A点 取为杆上受載部分的端点时,得c=0,b=1,e cos Bc=1. 設1很大,又得e-86 cosBb≈0.于是y=g/2;即挠度現在只 有上面求得之值的一半! 「同样,用式(4)能导出A点的弯矩表达式,如A点位于梁上受 载部分之外,而b和c分别表示此点到梁上受载部分两端的較大 和較小距离,則A点的挠度为 c sin B) 883EI. gdz e-Br cosBx sinBx) Jo 88EI -4(e-B cosBc-e-B6 cosB5). (h) 2k 当c=0而b=1很大时,得挠度 为9/2?,此与我們上面的結論符 合.当距离b和c增加时,式(h) 的挠度减小,随五和c的渐增而趋 于零 运用单个载荷的解式(3)也可