
Example We see that y1(x)=cosx and y2(x)=sinx are two solutions of y"+y=0 and y(x)=3cosx-2sinx is also a solution and satisfies y(0)=3,y/(0)=-2 This is the unique solution with these initial conditions. 4日10y至,无2000
Example We see that y1(x) = cos x and y2(x) = sinx are two solutions of y 00 +y = 0 and y(x) = 3 cos x−2 sinx is also a solution and satisfies y(0) = 3, y 0 (0) = −2 This is the unique solution with these initial conditions

Example Verify that y1(x)=et and y2(x)=xe are solutions of y"-2y+y=0 then find a solution satisfying y(0)=3,y(0)=1. Solution:We impose initial condition on the general solution y(x)=cie+caxe for which y(x)=(c1+c2)e*+c2xe* to obtain the simultaneous equations y(0)=c1=3, y(0)=c1+c2=1
Example Verify that y1(x) = e x and y2(x) = xex are solutions of y 00 −2y 0 +y = 0 then find a solution satisfying y(0) = 3, y 0 (0) = 1. Solution: We impose initial condition on the general solution y(x) = c1e x +c2xex for which y 0 (x) = (c1 +c2)e x +c2xex to obtain the simultaneous equations ( y(0) = c1 = 3, y 0 (0) = c1 +c2 = 1
Example We have c1=3,c2 =-2.Hence,the solution is y(x)=3e-2xex 4口0y至,无2000
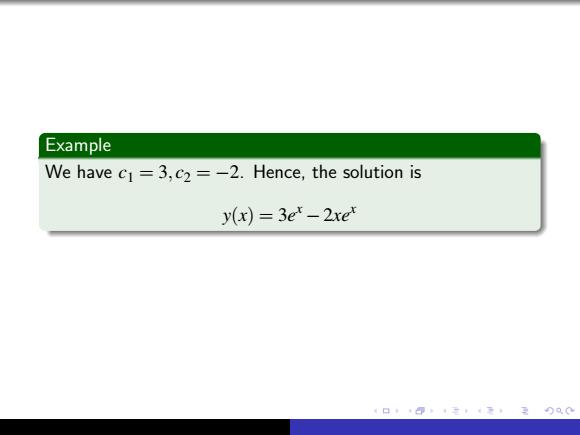
Example We have c1 = 3, c2 = −2. Hence, the solution is y(x) = 3e x −2xex

To find the unique solution to the IVP Jy"+p(x)y+q(x)y=0, y(a)=bo,y(a)=b1. 1口1日,4克1元000
To find the unique solution to the IVP ( y 00 +p(x)y 0 +q(x)y = 0, y(a) = b0, y 0 (a) = b1. Firstly, we find two essentially different solutions y1 and y2; Secondly, impose the initial conditions y(a) = b0, y 0 (a) = b1 on the general solution y(x) = c1y1 +c2y2 to get the simultaneous equations ( c1y1(a) +c2y2(a) = b0, c1y 0 1 (a) +c2y 0 2 (a) = b1. for the coefficients c1 and c2

To find the unique solution to the IVP [y"+p(x)y/+q(x)y=O, y(a)=bo,y(a)=b1. Firstly,we find two essentially different solutions y and y2; 4口y4元卡2月只0
To find the unique solution to the IVP ( y 00 +p(x)y 0 +q(x)y = 0, y(a) = b0, y 0 (a) = b1. Firstly, we find two essentially different solutions y1 and y2; Secondly, impose the initial conditions y(a) = b0, y 0 (a) = b1 on the general solution y(x) = c1y1 +c2y2 to get the simultaneous equations ( c1y1(a) +c2y2(a) = b0, c1y 0 1 (a) +c2y 0 2 (a) = b1. for the coefficients c1 and c2