
第十五章整数(线性)规划 ◆分枝定界法 ◆割平面法
第十五章 整数(线性)规划 ◆分枝定界法 ◆割平面法

整数(线性)规划(Integer Programming,P) 在线性规划问题的讨论中,有些最优解是小数,但 某些常要求最优解是整数(即整数解) 如决策变量是: 机器的台数、人数、车辆数等等 如果在问题中所有变量有整数限制,称:纯整数规划 或全整数规划) 如果问题中仅部分变量有整数限制,称:混合整数规划; 如果在问题中决策变量仅取0,1,称:0-1规划
整数(线性)规划 (Integer Programming, IP) 在线性规划问题的讨论中,有些最优解是小数,但 某些常要求最优解是整数(即整数解) 如决策变量是: 机器的台数、人数、车辆数等等 如果在问题中所有变量有整数限制,称:纯整数规划 (或全整数规划); 如果问题中仅部分变量有整数限制,称:混合整数规划; 如果在问题中决策变量仅取0,1,称:0-1规划
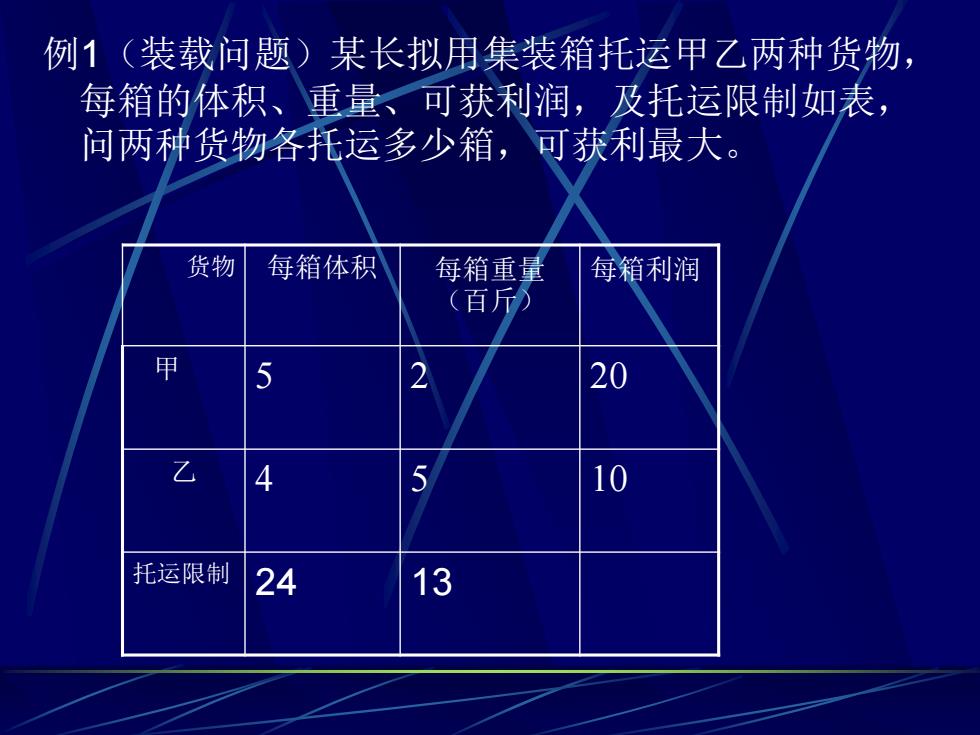
例1(装载问题)某长拟用集装箱托运甲乙两种货物, 每箱的体积、重量、可获利润,及托运限制如表, 问两种货物各托运多少箱,可获利最大。 货物 每箱体积 每箱重量 每箱利润 (百斤) 甲 5 2 20 乙 4 5 10 托运限制 24 13
例1(装载问题)某长拟用集装箱托运甲乙两种货物, 每箱的体积、重量、可获利润,及托运限制如表, 问两种货物各托运多少箱,可获利最大。 货物 每箱体积 每箱重量 (百斤) 每箱利润 甲 5 2 20 乙 4 5 10 托运限制 24 13

解:设x1,x2分别为甲、乙两种货物托运箱 数,则: max Z三20X1+10X2 s.t. 5x1+4X2≤24 2X1+5x2≤13 x1≥0,x2≥0.x1,x2为整数 这是一个纯整数规划问题
解: 设x1,x2分别为甲、乙两种货物托运箱 数,则: max Z = 20 x1 + 10 x2 s.t. 5x1 + 4x2 ≤ 24 2 x1 + 5x2 ≤ 13 x1 ≥ 0,x2 ≥ 0 .x1,x2为整数 这是一个纯整数规划问题
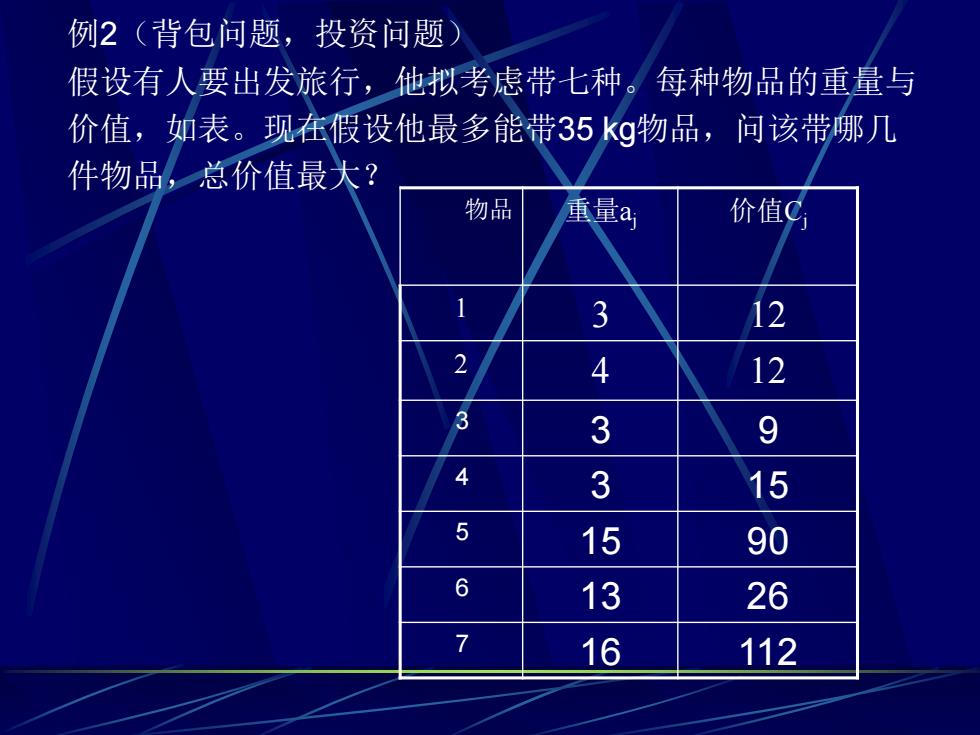
例2(背包问题,投资问题 假设有人要出发旅行,他拟考虑带七种。每种物品的重量与 价值,如表。现在假设他最多能带35kg物品,问该带哪几 件物品,总价值最大? 物品 重量a 价值C 1 2 34 12 12 3 3 9 4 3 15 5 15 90 6 13 26 7 16 112
例2(背包问题,投资问题) 假设有人要出发旅行,他拟考虑带七种。每种物品的重量与 价值,如表。现在假设他最多能带35 kg物品,问该带哪几 件物品,总价值最大? 物品 重量aj 价值Cj 1 3 12 2 4 12 3 3 9 4 3 15 5 15 90 6 13 26 7 16 112